第三章 图像的低通与高通滤波

---

前言

前面讲解了一些图像的基本理论以及操作，这一张将聚焦与图像的滤波操作。

一、卷积操作

解释：

图像卷积是一种在图像处理中广泛使用的操作。其基本思想是在图像的每个像素点上，以该点为中心选择一个固定大小的滤波器模板（通常是一个矩阵），并将该滤波器与该像素点及其相邻像素点进行卷积运算，生成一个新的像素值。通过将该滤波器模板与整张图像进行卷积操作，我们可以对图像进行一些线性操作，例如模糊、锐化、边缘检测等。

“卷积”这个术语最初是从数学领域中引入到信号和图像处理领域的。在数学中，卷积是两个函数之间的一种数学运算，它在函数之间进行加权平均的积分运算，可以用来描述信号在系统中的传递和变形过程。在信号和图像处理中，卷积操作的本质是一种加权平均的过程，它考虑不同像素对卷积结果的贡献程度，从而实现一些常见的图像处理操作。

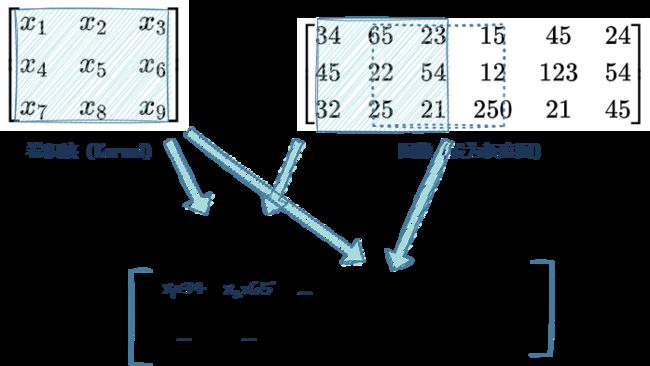
OpenCV中的一个函数----cv2.filter2D，可用于实现这种卷积运算操作。

cv2.filter2D函数的调用格式如下：

cv2.filter2D(src, ddepth, kernel, dst=None, anchor=None, borderType=None)

函数的参数解释如下：

• src：需要执行卷积操作的输入图像，可以是单通道或多通道图像。
• ddepth：输出图像的深度（即数据类型），通常设置为-1，表示和输入图像的深度相同。
• kernel：定义卷积操作的核，可以是任意大小的数组。
• dst：卷积操作的输出图像，可以选择是否使用。
• anchor：表示卷积核的锚点，通常设置为(-1, -1)，表示锚点位于核的中心。
• borderType：处理边界问题的方法，默认为cv2.BORDER_DEFAULT，表示默认使用边界反射。其它可选值包括cv2.BORDER_CONSTANT、cv2.BORDER_REPLICATE等。

注：边界像素周围可能不够卷积核的大小，因此边界需要进行边界扩展，这也就是filter2D中设置borderType参数的原因。

二、低通滤波

作用：

• 消除图片中的高斯噪声
• 消除图片中的椒盐噪声
• 图片模糊

高斯噪声是一种线性加性噪声，通常表示为服从高斯分布（正态分布）的随机变量的噪声。高斯噪声在图像处理中非常常见，特别是在图像传感器、摄像头、图像压缩等过程中，由于各种原因（如热噪声、传感器噪声、电子噪声、压缩算法噪声等），会产生随机干扰信号，从而引入高斯噪声。

椒盐噪声是一种常用的数字图像噪声模型，它是指在一幅图像中将一些像素点随机地变成纯黑色或纯白色。这种噪声通常是由于图像采集或传输中的信号干扰引起的，也可以是为了模拟真实世界中的图像失真而添加的。椒盐噪声会破坏图像的细节和纹理，导致图像质量下降，并使图像的分析和处理变得更为困难。

1. 方盒滤波与均值滤波

• 卷积核
  K = α [ 1 1 ⋯ 1 1 1 ⋯ 1 ⋮ ⋮ ⋯ ⋮ 1 1 ⋯ 1 ] h × w K = \alpha \begin{bmatrix} 1 & 1 & \cdots &1\\ 1 & 1 & \cdots &1\\ \vdots & \vdots & \cdots &\vdots\\ 1 & 1 & \cdots &1\\\end{bmatrix}_{h×w} K=α ​11⋮1​11⋮1​⋯⋯⋯⋯​11⋮1​ ​h×w​
• 当$\alpha =\frac{1}{h\times w}$时，该卷积核是实现均值滤波。当$\alpha$等于1时，该卷积实现的是方盒滤波，当像素值超出255时值为255。

# 方盒滤波
# normalize：正交化，一般都设置为 True，此时等同于均值滤波
cv2.boxFilter(src, ddepth, kernelSize:tuple[, dst[, anchor[, normalize[, borderType]]]]) -> dst

# 均值滤波
cv2.blur(src, kernelSize:tuple[, dst[, anchor[, borderType]]]) -> dst

2. 中值滤波

• 实现：对卷积核框住的像素值进行排序，取中间值作为输出结果。

  cv2.medianBlur(src, kernelSize:int[, dst]) -> dst
  

• 效果：适合去除椒盐噪声
  

3.高斯滤波

3.1 高斯分布

根据本科期间所学习的概率论可知，高斯分布是一种连续型的分布，具有概率密度函数，包括一维以及二维高斯分布：

• 一维高斯分布
  • 概率密度函数：$f(x)=\frac{1}{\sigma \sqrt[]{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$ ，其中$\mu$为样本均值，图像上表现为高峰的横坐标，$\sigma$为样本标准差，图像上表现为高峰的高度。标准差越大越不均匀，因此曲线比较平缓。
• 二维高斯分布
  -概率密度函数：$f(x,y)=\frac{1}{2\pi {\sigma }_x{\sigma }_y\sqrt{1-{\rho }^2}}\exp (-\frac{1}{2(1-{\rho }^2)}[\frac{(x-{\mu }_x{)}^2}{{\sigma }_x^2}+\frac{(y-{\mu }_y{)}^2}{{\sigma }_y^2}-\frac{2\rho (x-{\mu }_x)(y-{\mu }_y)}{{\sigma }_x{\sigma }_y}\left]\right)$，其中，$x$ 和 $y$ 表示二维空间中的横、纵坐标，${\mu }_x$ 和 ${\mu }_y$ 表示两个坐标轴上的均值，${\sigma }_x^2$ 和 ${\sigma }_y^2$ 分别表示两个方向上的方差，$\rho$ 表示两个方向上的相关系数。
  二维高斯分布太复杂，作如下假设：
  • ${\mu }_1={\mu }_2=0$
  • $\rho =0$
    得 $$f(x,y)=\frac{1}{2\pi {\sigma }_x{\sigma }_y}\exp (-\frac{1}{2}[\frac{x^2}{{\sigma }_x^2}+\frac{y^2}{{\sigma }_y^2}\left]\right)$$

3.2 滤波流程

1. 假定卷积核的中心坐标(x, y)为(0, 0)，然后得到周围的坐标值：
   
2. 将坐标值带入简化后的二维高斯分布概率密度函数，并取${\sigma }_1={\sigma }_2=1.5$：
   
3. 由于计算得到的值为概率密度，并非概率值，所以还需要转为概率。用每个值除以卷积核的总和得到概率值，从而得到高斯模板卷积核：
   
4. 整数高斯模板：所有高铝之除以左上角的概率值，然后四舍五入获得整数值，最后还要再归一化，前面加个$\frac{1}{所有整数和}$。

为啥需要整数的高斯模板我不太清楚。

5. 最后用获得的高斯模板卷积核进行卷积运算。

3.2 OpenCV代码及手动实现

• 手动实现高斯滤波：

  import numpy as np
  import cv2
  
  
  def naive_gaussian_blur(img, kernel_size, sigma):
      half_kernel_size = kernel_size // 2
      kernel = np.zeros((kernel_size, kernel_size), dtype=np.float32)
  
      constant = 1 / (2 * np.pi * sigma**2)
  
      for i in range(-half_kernel_size, half_kernel_size + 1):   #-2到2
          for j in range(-half_kernel_size, half_kernel_size + 1):
              kernel[i + half_kernel_size, j + half_kernel_size] = constant * np.exp(
                  -(i**2 + j**2) / (2 * sigma**2)
              )
  
      kernel /= kernel.sum()  #获取概率值
  
      output = np.zeros_like(img, dtype=np.float32)
  
      for x in range(half_kernel_size, img.shape[0] - half_kernel_size):
          for y in range(half_kernel_size, img.shape[1] - half_kernel_size):
              output[x, y] = np.sum(
                  img[
                      x - half_kernel_size : x + half_kernel_size + 1,
                      y - half_kernel_size : y + half_kernel_size + 1,
                  ]
                  * kernel
              )
  
      output = np.clip(output, 0, 255).astype(np.uint8)
  
      return output
  
  
  img = cv2.imread("F:/MyOpenCV/ai.jpg", cv2.IMREAD_GRAYSCALE)
  img = cv2.resize(img, (0, 0), fx=0.3, fy=0.3, interpolation=cv2.INTER_LINEAR)
  blurred_img = naive_gaussian_blur(img, kernel_size=5, sigma=2)
  cv2.imshow("Original Image", img)
  cv2.imshow("Blurred Image", blurred_img)
  cv2.waitKey(0)
  cv2.destroyAllWindows()
  

  

• OpenCV高斯滤波接口：

# sigmaX ：x 的标准差，不指定的话，根据 kernelSize 进行计算
# sigmaY ：y 的标准差，默认等于 sigmaX 
cv2.GaussianBlur(src, kernelSize:tuple, sigmaX[, dst[, sigmaY[, borderType]]]) -> dst

4. 双边滤波

4.1 原理

• 原因： 高斯滤波在除去高斯噪声的同时，也会不加区分的将图像中的边缘一并给加权平均了，所以就导致图片整体看起来很模糊。为了保护边缘，就产生了双边滤波算法。
• 图像边缘： 边缘的产生就是因为相邻的像素的颜色通道差别太大，因此，对相邻像素的颜色做差，就能标记出边缘（差值越大，就说明边缘的可能性越大）
• 算法思路： 在高斯滤波的基础上再添加一个灰度距离权重。灰度距离越大，灰度距离的权重越小，这样像素在高斯模糊中的占比就越小，进而实现只对颜色相近的像素进行高斯滤波。
• 当对图像进行双边滤波处理时，可以在每个像素处应用以下公式：

$$I_{\text{filtered}}(x,y)=\frac{1}{W_p}\sum _{j\in \Omega }{I}_j{w}_p(x,y)w_c(||I_j-I_{x,y}||)$$

其中，$I_{\text{filtered}}(x,y)$ 表示处理后的图像像素值，$I_j$ 表示邻域内每个像素的像素值，$w_p$ 表示位置权重函数，$w_c$ 表示颜色相似度权重函数，$||I_j-I_{x,y}||$ 表示两个像素之间的差异。

位置权重函数 $w_p$ 基于邻域内像素相对于当前像素的空间距离进行计算，通常采用高斯函数来表示，公式如下：

$$w_p(x,y)=e^{-\frac{||P_j-P_{x,y}|{|}^2}{2{\sigma }_p^2}}$$

其中，$P_j$ 是邻域内像素的二维位置，$P_{x,y}$ 是当前像素点的二维位置，${\sigma }_p$ 是距离参数（用于平衡空间距离的贡献）。

颜色相似度权重函数 $w_c$ 是基于像素值之间的相似程度来计算的，通常也采用高斯函数来表示，公式如下：

$$w_c(||I_j-I_{x,y}||)=e^{-\frac{||I_j-I_{x,y}|{|}^2}{2{\sigma }_c^2}}$$

其中，${\sigma }_c$ 是颜色空间的参数，用于平衡颜色相似度的贡献。

总权重 $W_p$ 是位置权重和颜色相似度权重的乘积，即：

$$W_p=\sum _{j\in \Omega }{w}_p(x,y)w_c(||I_j-I_{x,y}||)$$

将 $W_p$ 代入第一个公式中，即可计算出每个像素点的双边滤波值，从而得到处理后的图像。

4.2 OpenCV代码实现

# sigmaColor：sigma_s，高斯分布的标准差
# sigmaSpace：sigma_r，灰度距离的控制值 
cv2.bilateralFilter(src, kernelSize:int, sigmaColor, sigmaSpace[, dst[, borderType]]) -> dst

二、高通滤波

功能：

• 边缘检测
• 图像边缘：图像的灰度图中，相邻像素灰度值差距较大的位置。

1. Sobel算子

• 原理：对图像邻近的灰度像素进行求导，斜率较大的地方，边缘的概率最大。

• 差分法：图像中近似求导的方法
  $$I^{\prime }(x_i)=\frac{I(x_{i+1})-I(x_i)}{x_{i+1}-x_i}$$
  这里只对像素的一个方向进行求偏导（x方向或者y方向）。求导的实际操作仍然是卷积操作，所以对于分母差值也可以省略掉（因为对于同一个卷积核来说左右或者上下的差值是固定的）$$I^{\prime }(x_i)=I(x_{i+1})-I(x_i)$$

• 卷积核：

  • x方向求偏导：提取竖向的边缘，目标像素左右端的像素进行差值计算
    G x = [ − 1 0 + 1 − 2 0 + 2 − 1 0 + 1 ] G_x = \begin{bmatrix} -1 & 0& +1 \\-2 & 0 & +2 \\-1 & 0 &+1\end{bmatrix} Gx​= ​−1−2−1​000​+1+2+1​ ​
  • y方向求偏导：提取横向的边缘，目标像素上下端的像素进行差值计算
    G y = [ − 1 − 2 − 1 0 0 0 + 1 + 2 + 1 ] G_y = \begin{bmatrix} -1 & -2& -1 \\0 & 0 & 0 \\+1 & +2 &+1\end{bmatrix} Gy​= ​−10+1​−20+2​−10+1​ ​

# ddepth：cv2.CV_， 结果图像的位深
# dx：对 x 方向求偏导
# dy：对 y 方向求偏导
# ksize：卷积核大小
cv2.Sobel(src, ddepth, dx:bool, dy:bool[, dst[, ksize:int[, scale[, delta[, borderType]]]]]) -> dst
# src中的数据取绝对值
cv2.convertScaleAbs(src[, dst[, alpha[, beta]]]) -> dst

• sobel计算，会导致像素值为负，因此输出图像的位深ddepth应当使用有符号类型，例如cv2.CV_16S、cv2.CV32F等。
• 颜色通道数值不存在负数，所以还需要对计算结果取绝对值convertScaleAbs。
• 对于横向、竖向的边界要分两次进行，一起提取效果会很差，具体原因见下方。

分开提取边界原因：这是因为在对一个多元函数同时对不同自变量求导时，往往忽略了它们之间的相互影响和依存关系。具体来说，如果一个函数包含$x$和$y$两个变量，那么对$x$求导时会把$y$看作常数而忽略其对$x$的影响；同样地，对$y$求导时会把$x$看成常数而忽略其对$y$的影响。

2. Schar算子

• 介绍：对Sobel算子的改进。
• 卷积核：卷积核大小固定3×3
  • x方向求偏导：提取竖向的边缘，目标像素左右的像素进行差值计算
    G x = [ − 3 0 + 3 − 10 0 + 10 − 3 0 + 3 ] G_x = \begin{bmatrix} -3 & 0& +3 \\-10 & 0 & +10 \\-3 & 0 &+3\end{bmatrix} Gx​= ​−3−10−3​000​+3+10+3​ ​
  • y方向求偏导：提取横向的边缘，目标像素上下的像素进行差值计算
    G y = [ − 3 − 10 − 3 0 0 0 + 3 + 10 + 3 ] G_y = \begin{bmatrix} -3 & -10& -3 \\0 & 0 & 0 \\+3 & +10 &+3\end{bmatrix} Gy​= ​−30+3​−100+10​−30+3​ ​

OpenCV相关接口：

cv2.Scharr(src, ddepth, dx, dy[, dst[, scale[, delta[, borderType]]]]) -> dst

3.拉普拉斯算子

• 思想： Sobel算子是对像素求解一阶导数，最大值处就是边缘；对一阶导数再求导，那么零值处就是边缘，但是，由于利用差分进行计算而且像素点也是离散的，进度丢失大，这个“零”的表现其实不明显。边界显示的还是主要两边的峰值。

• 拉普拉斯算子定义：
  $${▽}^{2}f=\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}$$

    拉普拉斯算子能表示一个空间曲面的平坦程度，至于为什么这样定义我没有细究。
  

• 二阶差分：
  f(x,y)对x右侧的一阶偏导(因为相邻点像素距离差为1，所以分母为1略去)：
  $$\frac{\partial f}{\partial x}=f(x+1,y)-f(x,y)$$
  f(x,y)对x左侧的一阶偏导（同上）：
  $$\frac{\partial f}{\partial x}=f(x,y)-f(x-1,y)$$
  f(x,y)对x的二阶偏导(右侧一阶减左侧一阶，分母仍然是1略去)：
  $$\begin{array}{rl}\frac{{\partial }^{2}f}{\partial x^2}& =f(x+1,y)-f(x,y)-(f(x,y)-f(x-1,y))\\ & =f(x+1,y)+f(x-1,y)-2f(x,y)\end{array}$$
  f(x,y)对y的二阶偏导（同上）：
  $$\begin{array}{rl}\frac{{\partial }^{2}f}{\partial y^2}& =f(x,y+1)-f(x,y)-(f(x,y)-f(x,y-1))\\ & =f(x,y+1)+f(x,y-1)-2f(x,y)\end{array}$$
  上面两式相加得到结果：
  $$\begin{array}{rl}{▽}^{2}f& =f(x+1,y)+f(x-1,y)-2f(x,y)+f(x,y+1)+f(x,y-1)-2f(x,y)\\ & =(f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1))-4f(x,y)\end{array}$$

写成矩阵形式：
I ′ ′ ( x i , y i ) = [ 0 1 0 1 − 4 1 0 1 0 ] ∗ [ I ( x i − 1 , y i − 1 ) I ( x i , y i − 1 ) I ( x i + 1 , y i − 1 ) I ( x i − 1 , y i ) I ( x i , y i ) I ( x i + 1 , y i ) I ( x i − 1 , y i + 1 ) I ( x i , y i + 1 ) I ( x i + 1 , y i + 1 ) ] \mathrm{I}^{\prime \prime}\left(\mathrm{x}_{\mathrm{i}}, \mathrm{y}_{\mathrm{i}}\right)=\left[\begin{array}{ccc}0 & 1 & 0 \\1 & -4 & 1 \\0 & 1 & 0\end{array}\right] *\left[\begin{array}{ccc}\mathrm{I}\left(\mathrm{x}_{\mathrm{i}-1}, \mathrm{y}_{\mathrm{i}-1}\right) & \mathrm{I}\left(\mathrm{x}_{\mathrm{i}}, \mathrm{y}_{\mathrm{i}-1}\right) & \mathrm{I}\left(\mathrm{x}_{\mathrm{i}+1}, \mathrm{y}_{\mathrm{i}-1}\right) \\\mathrm{I}\left(\mathrm{x}_{\mathrm{i}-1}, \mathrm{y}_{\mathrm{i}}\right) & \mathrm{I}\left(\mathrm{x}_{\mathrm{i}}, \mathrm{y}_{\mathrm{i}}\right) & \mathrm{I}\left(\mathrm{x}_{\mathrm{i}+1}, \mathrm{y}_{\mathrm{i}}\right) \\\mathrm{I}\left(\mathrm{x}_{\mathrm{i}-1}, \mathrm{y}_{\mathrm{i}+1}\right) & \mathrm{I}\left(\mathrm{x}_{\mathrm{i}}, \mathrm{y}_{\mathrm{i}+1}\right) & \mathrm{I}\left(\mathrm{x}_{\mathrm{i}+1}, \mathrm{y}_{\mathrm{i}+1}\right)\end{array}\right] I′′(xi​,yi​)= ​010​1−41​010​ ​∗ ​I(xi−1​,yi−1​)I(xi−1​,yi​)I(xi−1​,yi+1​)​I(xi​,yi−1​)I(xi​,yi​)I(xi​,yi+1​)​I(xi+1​,yi−1​)I(xi+1​,yi​)I(xi+1​,yi+1​)​ ​

• 效果：拉普拉斯算子处理渐变图的能力要强于Sobel算子

cv2.Laplacian(src, ddepth:cv2.CV_[, dst[, ksize:int[, scale[, delta[, borderType]]]]]) -> dst

4. Canny边缘检测

4.1 算法流程

4.1.2 图像降噪

图像降噪主要采用高斯滤波方式对图像进行降噪,公式描述如下，
$$I_g=G\ast I$$
其中，$I_g$表示高斯滤波后的像素值，$G$表示高斯滤波卷积核，$I$表示原像素。

4.1.3 计算梯度

1. 利用Sobel算子，计算x, y方向的梯度:
   $$\begin{gathered} I_{sx}=G_x\ast I_g \\ {I}_{sy}=G_y\ast I_g \end{gathered}$$
2. 计算每个像素的梯度强度：
   $$I_s=\sqrt{I_{sx}^2+I_{sy}^2}\approx \left|I_{sx}\right|+\left|I_{sy}\right|$$
3. 计算每个像素的梯度方向：
   $$\theta =arctan(\frac{I_{sy}}{I_{sx}})$$

4.1.4 非极大值抑制

得到的每个像素强度的非局部最大值就全部舍弃掉，进行边缘预选。
有两种方法：

• 线性插值法： 对比$I_s$与$I_1、I_2$的值，若$I_s$最大，则保留作为边界，否则则舍弃掉。
  
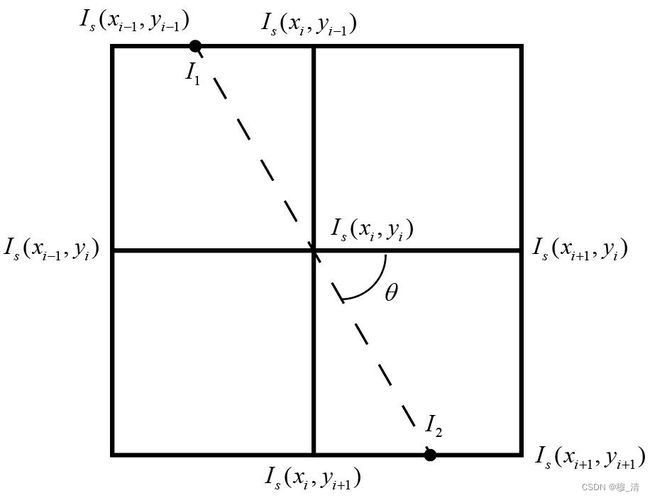
  I_1,I_2的计算如下：
  
• 角度近似法： 将中心点周围的像素分为8个方向如下图，刚好每个方向对应的点都是非亚像素点，已知其对应的梯度强度，看中心点的梯度方向$\theta$离哪个方向近就用哪个像素点强度作对比，若中心点大就保留。
  

4.1.5 双阈值检测

用来确定最终的边缘。

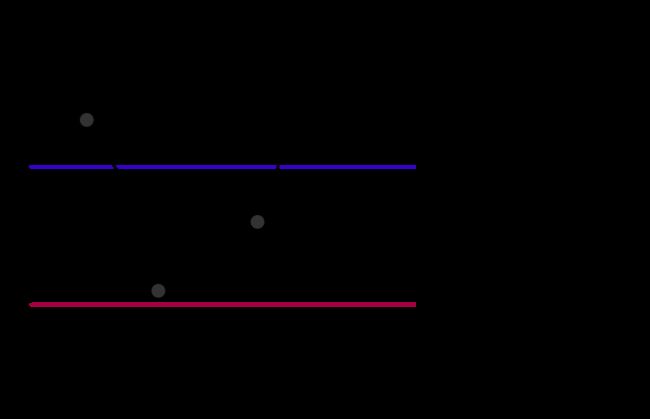
梯度>maxVal：认为是边界像素
梯度 梯度介于两者之间判断是否和边界连着，若连着则保留，例如C保留，B舍弃。

判断是否连接会用到DFS或BFS的图的搜索遍历算法，只要周围点中有强边界像素则判其为连接。

4.2 OpecvCV代码

#  threshold1：minVal
# threshold2：maxVal
cv2.Canny(image, threshold1, threshold2[, edges[, apertureSize[, L2gradient]]]) -> edges

总结

本章主要讲解了卷积操作的基本知识以及低通滤波和高通滤波，低通滤波就是为了消除图像的噪声，但也会让图像变的模糊；高通滤波能够检测图像的边缘，从而进行其他的判断。