使用RobustPCA 进行时间序列的异常检测
鲁棒主成分分析(Robust Principal Component Analysis, RobustPCA)是一种将时间序列矩阵分解为低秩分量和稀疏分量的技术。这种分解能够识别潜在的趋势,以及检测异常和异常值。在本中我们将研究RobustPCA的数学基础,介绍它与传统的PCA之间的区别,并提供可视化来更好地理解它在时间序列预测和异常检测中的应用。
RobustPCA 的数学基础
RobustPCA是经典主成分分析(PCA)的扩展,它可以通过捕获主成分来找到高维数据的低维表示。经典PCA对异常值敏感,在噪声存在时可能表现不佳。而RobustPCA通过将时间序列矩阵分解为两个组件来解决这个问题:捕获潜在趋势的低秩组件和解释异常值的稀疏组件。
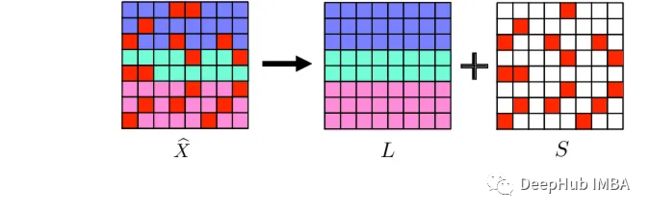
在给定一个时间序列矩阵X, RobustPCA分解可表示为:
X = L + S
这里的,L为低秩分量,S为稀疏分量。
RobustPCA解决了以下优化问题来寻找L和S:
这里的||L||*表示L的核范数(即其奇异值的和),||S||_1表示S的L1范数(即其元素的绝对值的和),λ是一个正则化参数,用于平衡低秩分量和稀疏分量之间的权衡。
RobustPCA 与传统PCA的区别
RobustPCA和传统的PCA(Principal Component Analysis)都是用于矩阵分解的技术,但它们在处理数据中包含噪声和异常值时的表现有所不同。
传统PCA是一种线性变换技术,用于将高维数据集投影到低维子空间中,以便更好地理解和分析数据。传统PCA假设数据中的每个观测值都服从高斯分布,这意味着在存在异常值或噪声的情况下,传统PCA的性能会受到影响。
而RobustPCA在数据包含噪声和异常值时表现更好,因为它能够将数据分解为低秩和稀疏成分。这使得RobustPCA在许多应用中比传统PCA更具有实用价值。例如,RobustPCA可以用于在图像和视频中检测和移除噪声和异常值,而传统PCA则可能会将噪声和异常值错误地归因于数据的基本结构。
另一个区别是,传统PCA是一个凸优化问题,可以通过求解特征值分解来直接求解,而RobustPCA是一个非凸优化问题,需要使用迭代算法(例如交替方向乘子法ADMM)来求解。此外传统PCA通常对数据进行中心化处理,而RobustPCA可以处理未中心化的数据。
RobustPCA使用示例
在Python中,robust_pca包提供了一个易于使用的基于ADMM算法的RobustPCA实现。
下面是一个使用robust_pca包来分解时间序列矩阵X的例子:
import numpy as np
from robust_pca import RobustPCA
# Create a sample time series matrix X
np.random.seed(42)
X = np.random.randn(100, 10)
# Perform RobustPCA decomposition
rpca = RobustPCA(lam=0.1)
L, S = rpca.fit_transform(X)
为了更好地理解RobustPCA分解,我们可以可视化原始时间序列矩阵X、低秩分量L和稀疏分量s。这种可视化可以帮助我们评估RobustPCA在从异常值和噪声中分离潜在趋势方面的有效性。
在上面的例子中,我们可以看到低秩分量L捕获了平滑趋势,而稀疏分量S隔离了异常值和噪声。
RobustPCA的应用
鲁棒主成分分析可以应用于广泛的时间序列预测和异常检测任务,包括:
金融市场分析:RobustPCA可用于分析高维金融时间序列数据,如股票价格、交易量和经济指标。通过将数据分解为低秩和稀疏的组件,我们可以识别趋势和异常,为投资决策和风险管理策略提供信息。
能源需求预测:RobustPCA可以通过捕捉数据中的潜在趋势和季节性来帮助预测能源需求,同时考虑极端天气事件或设备故障造成的异常值。
传感器数据分析:在工业应用中,RobustPCA可用于分析传感器数据,检测可能表明设备故障或其他问题的异常情况。
总结
鲁棒主成分分析(Robust Principal Component Analysis, RobustPCA)是一种将时间序列矩阵分解为低秩分量和稀疏分量的强大技术。这种分解允许在存在噪声和异常值的情况下进行更准确的趋势估计和异常检测,在科学和工程的各个领域中具有许多实际应用。
https://avoid.overfit.cn/post/0a8c32f16a284ceba20dee9cdf858ecb
作者:Naveen Kaushik