数据结构——栈，队列和数组

一 栈

1 基本概念

栈是一种线性表，但是只能在一端插入或者删除，而且栈是先进后出（后进先出）的

n个不同元素的排列个数有1/(n+1)*C_2nⁿ

基本操作：

Initstack(&S);           \\初始化一个空栈
Stackempty(S);           \\判空
push(&S,X);              \\进栈
pop(&s,&x);              \\出栈
gettop(&s,&x);           \\读栈顶元素
destroystack(&s);        \\销毁栈

2 栈的顺序存储结构

2.1 顺序栈的实现

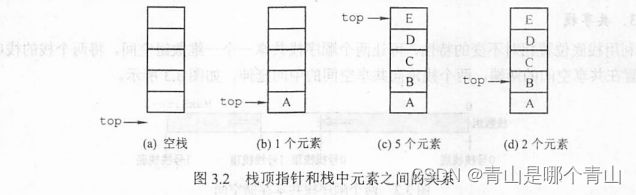
采用顺序存储，利用一组地址连续的存储单元存放，设一个指针指示当前栈顶元素的位置

#define maxsize 50
typedef struct
{
    elemtype data[maxsize];
    int top;                        \\初始为-1
}Sqstack;

受数组上限的约束，可能发生溢出

2.2 顺序栈的基本运算

（1）初始化

viod Initstack(sqstack &s)
{
      s.top=-1;
}

（2）判空

bool stackempty(sqstack &s)
{
     if(s.top==-1)
         return true;
     else
         return false;
}

（3）进栈

bool push(sqstack &s,elemtype x)
{
        if(s.top==maxsize-1)
           return false;
        s.data[++s.top]=x;
        return true;
}

（4）出栈

bool pop(sqstack &s,elemtype &x)
{
      if(s.top==-1)
          return false;
      x=s.data[s.top--];
      return true;
}

（5）读栈顶元素

bool gettop(sqstack s,elemtype &x)
{
     if(s.top==-1)
         return false;
     x=s.data[s.top];
     return true;
}

2.3 共享栈

两个顺序栈共享一个一维数组

top0=-1时0号栈为空，top1=maxsize时1号栈为空

仅当两个栈顶指针相邻，top1-top0=1时，栈满

0号栈进栈，top0先加1再赋值；1号栈进栈top1先减1再赋值；出栈时相反

3 栈的链式存储结构

称为链栈，便于多个栈共享存储空间和提高效率，且不存在栈满上溢的情况，通常用单链表实现，规定所有操作在表头进行

没有头结点，Lhead指向栈顶元素

typedef struct Linknode
{
    elemtype data;
    struct  Linknode  *next;
}*Listack;

二 队列

1 基本概念

也是一种操作受限的线性表，但是只允许一端插入，一端删除，即先进先出

Initqueue(&Q);            \\初始化
Queueempty(Q);            \\判空
Enqueue(&Q,x);            \\入队
Dequeue(&Q,&x);           \\出队
Gethead(Q,&x);            \\读队头元素

栈和队列都不能随意读取中间的元素

2 队列的顺序存储结构

2.1 队列的顺序存储

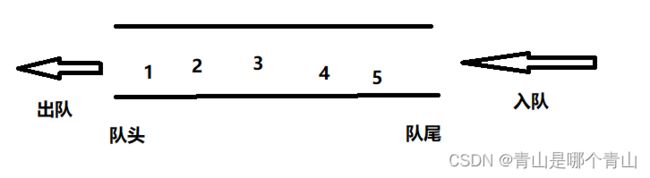
分配一块连续的存储单元，设两个指针，队头指针front指向队头元素，队尾指针rear指向队尾元素的下一个位置

#define maxsize 50
typedef struct
{
    elemtype data[maxsize];
    int front,rear;            \\初始都为0
}Sqqueue;

不能用Q.rear==maxsize来判断队列满的条件，如图

2.2 循环队列

由顺序队列的缺点，引出循环队列

将顺序队列臆造为一个环状的空间，即把存储队列元素的表从逻辑上视为一个环，利用除法取余运算来实现

队首指针进1：Q.front=(Q.front+1)%maxsize

队尾指针进1：Q.rear=(Q.rear+1)%maxsize

队列长度：（Q.rear+maxsize-Q.front）%maxsize

出队入队时指针都要按顺时针方向进1

判空可以用Q.front=Q.rear，但是满队时也有Q.front=Q.rear，如图

区分队空还是队满的解决方法：

（1）牺牲一个单元来区分，入队时少用一个队列单元，约定以队头指针再队尾指针的下一个位置作为队满的标志

队满：(Q.rear+1)%maxsize==Q.front

队空：Q.front==Q.rear

队列元素的个数：（Q.rear+maxsize-Q.front）%maxsize

（2）增设表示元素个数的成员size

队空：Q.size==0

队满：Q.size == maxsize

两种情况都有Q.front==Q.rear

（3）增设tag数据成员

tag=0，若因删除导致Q.front==Q.rear，队空

tag=1，若因插入导致Q.front==Q.rear，队满

2.3 循环队列的操作

（1）初始化

void Iinitqueue(Sqqueue &Q)
{
     Q.rear=Q.front=0;
}

（2）判空

bool isempty(Sqqueue Q)
{
    if(Q.rear==Q.front)
        return true;
    else
        ruturn false;
}

（3）入队

bool Enqueue(Sqqueue &Q,elemtype x)
{
    if((Q.rear+1)%maxsize == Q.front)
        return false;
    Q.data[Q.rear]=x;
    Q.rear=(Q.rear+1)%maxsize;
    return true;
}

（4）出队

bool Dequeue(Sqqueue &Q,elemtype &x)
{
    if(Q.rear == Q.front)
        return false;
    x=Q.data[Q.front];
    Q.front=(Q.front+1)%maxsize;
    return true;
}

3 队列的链式存储结构

3.1 队列的链式存储

实际上是一个同时带有队头指针和队尾指针的单链表，头指针指向队头结点，尾指针指向队尾结点，即单链表的最后一个结点

typedef struct Linknode           \\队列结点
{
     elemtype data;
     struct Linknode *next;
}Linknode;

typedef struct                    \\链式队列
{
   Linknode *front,*rear;
}*LinkQueue;

Q.front==NULL，Q.rear==NULL时队列为空

通常设计为带头结点，统一删除和插入操作；适合于数据元素变动比较大的情形

3.2 链式队列的基本操作

（1）初始化

void Initqueue(Linkqueue &Q)
{
    Q.front = Q.rear=(Linknode*)malloc(sizeof(Linknode));   \\建立头结点
    Q.front->next=NULL;                                     \\初始为空
}

（2）判空

bool isempty(Linkqueue Q)
{
    if(Q.front==Q.rear)
        return true;
    else
        return false;
}

（3）入队

void Enqueue(Linkqueue &Q,elemtype x)
{
    Linknode *s=(Linknode*)malloc(sizeof(Linknode));
    s->data=x;
    s->next=NULL;
    Q.rear->next=s;
    Q.rear=s;
}

（4）出队

bool Dequeue(Linkqueue &Q,elemtype &x)
{
    if(Q.front == Q.rear)
        return false;
    Linknode *p=Q.front->next;
    x=p->data;
    Q.front->next=p->next;
    if(Q.rear==p)
        Q.rear=Q.front;
    free(p);
    return true;
}

4 双端队列

允许两端都可以进行入队和出队操作，逻辑结构仍是线性结构

输出受限：

输入受限：

三 栈和队列的应用

1 栈的括号匹配问题

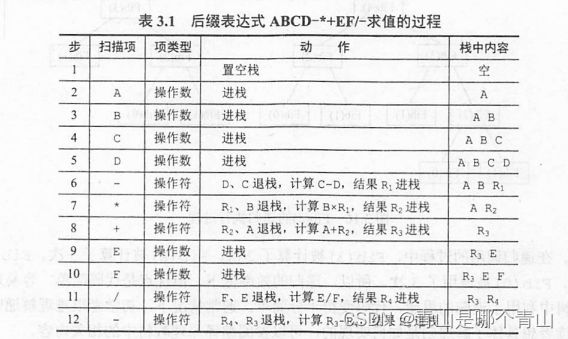
2 栈的表达式求值问题

3 栈的递归问题

int fib(int n)                      \\递归实现斐波那契数列
{
     if(n==0)
         return 0;
    else if (n==1)
        return 1;
    else
        return fib(n-1)+fib(n-2);
}

但是递归次数过多容易造成栈溢出，转换为非递归需要借助栈

4 队列的层序遍历问题

5 队列的计算机系统的应用

（1）解决主机与外部设备之间速度不匹配的问题

设置一个数据缓冲区，这个缓冲区存储数据就是一个队列

（2）解决多用户引起的资源竞争问题

按请求的先后顺序入队

四 数组和特殊矩阵

1 数组

数组是线性表的推广，以为数组可视为一个线性表，二维数组可视为其元素也是定长线性表的线性表

对于多维数组，有两种存储映射方式，按行优先和按列有限

2 特殊矩阵的压缩存储

压缩存储：为多个值相同的元素只分配一个存储空间，对零元素不分配空间

常见的特殊矩阵：对称矩阵，上（下）三角矩阵，对角矩阵

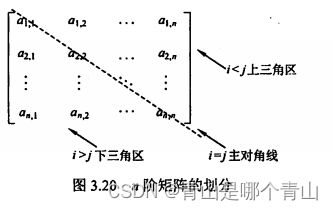
2.1 对称矩阵

元素下标的对应关系：

k=i(i-1)/2+j-1，i$⩾$j，下三角区和主对角线元素

k=j(j-1)/2+i-1，iij=a_ji

下标从1开始

2.2 三角矩阵

下三角矩阵：

k=i(i-1)/2+j-1，i$⩾$j，下三角区和主对角线元素

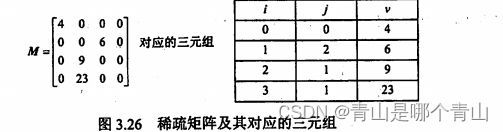
k=n(n+1)/2，i

上三角矩阵：

k=(i-1)(2n-i+2)/2+j-i，i$⩽$j，上三角区和主对角线元素

k=n(n+1)/2，i>j，下三角区元素（常数项）

下标从0开始

2.3 三对角矩阵

下标：k=2i+j-3

反之若知道k，则 i=(k+1)/3+1,向下取整

j=k-2i+3

2.4 稀疏矩阵

矩阵中非零个数非常少

为节省空间，将非零元素和相应的行和列构成一个三元组（行，列，值）

但是不能随机存取