Python3数据分析与挖掘建模(11)复合分析-分组分析与实现示例
1. 分组分析
1.1 概述
分组与钻取是数据分析中常用的技术,用于对数据进行聚合和细分分析。它可以帮助我们从整体数据中获取特定维度的汇总信息,并进一步钻取到更详细的子集数据中进行深入分析。
分组(Grouping)是指根据某个或多个特征将数据集分成多个组或类别。通过对数据进行分组,我们可以计算每个组的统计量(如平均值、总和、计数等),并进行比较、汇总或进一步分析。
钻取(Drilling)是指在分组的基础上,进一步细分数据集,以便更深入地了解特定组或类别的情况。通过钻取操作,我们可以选择特定的分组或类别,并对其进行详细分析,例如计算其子组的统计量、绘制子组的图表等。
在实际应用中,分组与钻取常常结合使用。首先,我们根据某个或多个特征将数据集进行分组,得到分组的汇总统计量。然后,我们可以选择特定的分组,进行钻取操作,深入分析该分组的子集数据,以获取更详细的信息和洞察。
例如,假设我们有一个销售数据集,包含产品名称、销售额、销售地区等信息。我们可以首先根据地区进行分组,计算每个地区的总销售额和平均销售额。然后,我们可以选择某个特定地区,钻取到该地区的子集数据,进一步分析该地区的销售趋势、热门产品等详细信息。
分组与钻取是数据分析中非常灵活和强大的工具,可以帮助我们从整体数据中提取有价值的信息,并深入挖掘数据的细节。它在数据汇总、对比、筛选和洞察等方面具有广泛的应用。
1.2 向上与向下钻取
向上钻取(Drill-Up)和向下钻取(Drill-Down)是在数据分析中进行层级切换的操作。
向上钻取(Drill-Up)是指从较低层级的数据汇总层级切换到较高层级,以获取更广泛的视角和总体概述。通过向上钻取,我们可以从细分的数据汇总层级上升到更高级别的聚合,获取更广泛的汇总信息。这有助于我们了解数据的整体趋势、总体性能等。
举例来说,假设我们有一个销售数据集,包含产品的销售额按年、季度和月份进行了分组汇总。如果我们当前处于月份级别的细分数据,通过向上钻取,我们可以切换到季度级别或年度级别,以获取更高层级的销售额总和和平均值,从而获得更宏观的销售趋势和总体表现。
向下钻取(Drill-Down)则是相反的操作,它是从较高层级的数据汇总层级切换到较低层级,以获得更详细的细分数据。通过向下钻取,我们可以深入到更细致的数据层级,以获取更详细、具体的信息。
继续以上面的例子,假设我们当前处于季度级别的销售数据汇总,通过向下钻取,我们可以切换到月份级别的细分数据,以查看每个季度内各个月份的销售情况,进一步分析季度内的销售趋势和波动情况。
向上钻取和向下钻取是在数据分析中进行层级切换和数据细化的常用操作。它们使分析人员能够根据需要在不同的层级之间切换,从整体和细节两个视角对数据进行深入理解和分析。这种灵活性和可操作性有助于发现数据中的模式、趋势和异常情况,并支持更有针对性的决策和行动。
1.3 连续分组
连续分组(Continuous Grouping)是一种数据分析方法,用于将连续变量划分为不同的组或区间,以便更好地理解数据的分布和趋势。通过连续分组,我们可以将连续变量按照一定的规则划分为若干个区间,然后分析每个区间内的数据特征和统计指标,如频数、均值、中位数等。这有助于我们识别出数据的特定模式、异常值和趋势,并提供对数据分布的更详细描述。
(1)分隔
分隔(一阶差分)是一种数据处理技术,用于计算连续变量在相邻数据点之间的差异或变化。一阶差分可以通过计算当前数据点与前一个数据点之间的差异来表示数据的变化趋势。这对于识别数据中的趋势、周期性和变化点非常有用。通过观察一阶差分的值,我们可以了解数据的增长或减少速度,以及变化的程度。
(2)拐点
拐点(二阶差分)是在一阶差分的基础上进行的进一步处理,用于检测数据变化的拐点或突变点。二阶差分计算的是一阶差分之间的差异,通过观察二阶差分的值,我们可以判断数据变化的趋势是否发生了明显的转折点或拐点。拐点分析可以帮助我们确定数据变化的阶段性特征,识别出数据中的重要变化点,并对数据的结构和趋势进行更精确的分析。
(3)聚类
聚类(Clustering)是一种无监督学习方法,用于将数据样本划分为不同的组或簇,使得同一组内的样本具有较高的相似性,而不同组之间的样本具有较大的差异性。聚类分析可以帮助我们发现数据中的内在模式和结构,将相似的数据点归为一类,并将不同的数据点分离开来。常用的聚类算法包括K-means聚类、层次聚类、DBSCAN等。通过聚类分析,我们可以识别出数据集中的群组、聚集或异常点,并洞察数据的特定模式和分布。
(4)不纯度
不纯度(Gini Impurity)是在决策树算法中用于衡量节点纯度的指标。在分类问题中,不纯度衡量了一个节点中样本的混杂程度,即该节点包含不同类别样本的程度。Gini Impurity通过计算每个类别在节点中的频率的
2. 不纯度(Gini系数)
2.1 概述
Gini系数是一种衡量不纯度的指标,常用于衡量分类问题中的类别不平衡程度。在机器学习和决策树算法中经常使用Gini系数来评估节点的纯度。
Gini系数的计算方法如下:
1. 首先,计算每个类别在数据集中的频率或比例。
2. 计算Gini系数的公式为:Gini = 1 - ∑(p^2) ,其中∑表示对所有类别求和,p表示每个类别的频率或比例。
3. Gini系数的取值范围为0到1,0表示数据集的纯度最高,即所有样本都属于同一类别;1表示数据集的纯度最低,即各类别的样本均匀分布。
在分类问题中,使用Gini系数可以评估不同特征的划分能力,选择具有较低Gini系数的特征作为划分点,以提高决策树的分类性能。
公式2: ![]()
2.2 分组分析
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as ss
import seaborn as sns
# 设置Seaborn绘图的上下文和字体大小
sns.set_context(font_scale=1.5)
# 读取HR.csv数据文件,并将数据存储在DataFrame对象df中
df = pd.read_csv("../data/HR.csv")
# 使用Seaborn绘制条形图,其中x轴为"salary"列,y轴为"left"列,hue参数表示按照"department"列进行分组
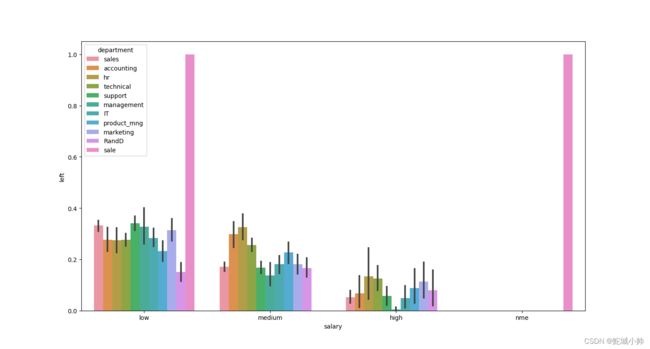
sns.barplot(x="salary", y="left", hue="department", data=df)
# 显示绘图结果
plt.show()
该代码使用了pandas、numpy、matplotlib.pyplot和seaborn库来进行数据处理和可视化。
-
sns.set_context(font_scale=1.5):设置Seaborn绘图的上下文,并将字体大小设置为1.5倍,用于调整绘图的整体样式。 -
df = pd.read_csv("../data/HR.csv"):通过pd.read_csv()函数读取名为"HR.csv"的数据文件,并将数据存储在DataFrame对象df中,用于后续的数据分析和可视化。 -
sns.barplot(x="salary", y="left", hue="department", data=df):使用Seaborn的barplot函数绘制条形图。其中,x="salary"表示将"salary"列作为x轴数据,y="left"表示将"left"列作为y轴数据,hue="department"表示按照"department"列进行分组。最终绘制出不同薪资水平下离职率的条形图,并根据部门进行分组和着色。 -
plt.show():显示绘制的条形图结果。
条形图结果:
从表中可以知道,市场部的工资与离职率很高。工资在中等收入的部门,Hr的离职率是最高的
2.3 连续值分析
# 设置绘图上下文的字体比例
sns.set_context(font_scale=1.5)
# 读取数据
df = pd.read_csv("../data/HR.csv")
# 获取满意度数据列
sl_s = df["satisfaction_level"]
# 创建x轴数据,使用长度范围
x_data = list(range(len(sl_s)))
# 创建y轴数据,对满意度数据进行排序
y_data = sl_s.sort_values()
# 使用sns.barplot绘制条形图,x轴为x_data,y轴为y_data
sns.barplot(x=x_data, y=y_data)
# 显示图形
plt.show()
sl_s代表了"satisfaction_level"列的数据,如果这列数据是连续值,那么sl_s也将是一个连续值的Series对象。
然后,在代码中使用sns.barplot绘制条形图时,将连续值的x_data作为x轴数据,这可能会导致图形不太准确或不易解释。通常,条形图更适用于展示类别型数据的分布,而对于连续值的分布,常用的方法是使用直方图(sns.histplot)或核密度估计图(sns.kdeplot)等。
因此,如果satisfaction_level是连续值的话,您可以考虑使用其他适合连续值的图形方法来展示其分布情况。
条形图结果:
如图,存在两个拐弯的点,可以通过对拐弯的点做界限进行分组分析