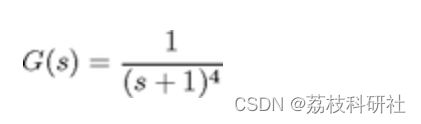【最优PID 整定】PID性能指标(ISE，IAE，ITSE和ITAE)优化、稳定性裕量(Matlab代码实现)

欢迎来到本博客❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

本文目录如下：

目录

1 概述

2 运行结果

​

3 参考文献

4 Matlab代码实现

---

1 概述

PID控制器是工业系统中使用最广泛的控制器。然而，适当地调整PID控制器并非易事，尽管它最多只有三个参数。

大多数PID整定规则基于工厂的一阶加延时假设，因此无法确保最佳控制性能。使用mordern优化技术，可以根据工厂的实际传递函数调整PID控制器，以优化闭环性能。

此提交包含一个功能，用于根据四个不同的性能指标（例如ISE，IAE，ITSE和ITAE）执行最佳PID设计。

PID控制器是各种工程系统中应用最广泛的控制器。但是，适当调整 PID 控制器不是一件容易的事，尽管它最多只有三个参数。困难部分来自一些 对控制系统性能的要求很高，部分是由于PID参数对控制的影响复杂 性能。此提交提供了有关使用稳定性裕度进行 PID 调谐的第二个教程。

2 运行结果

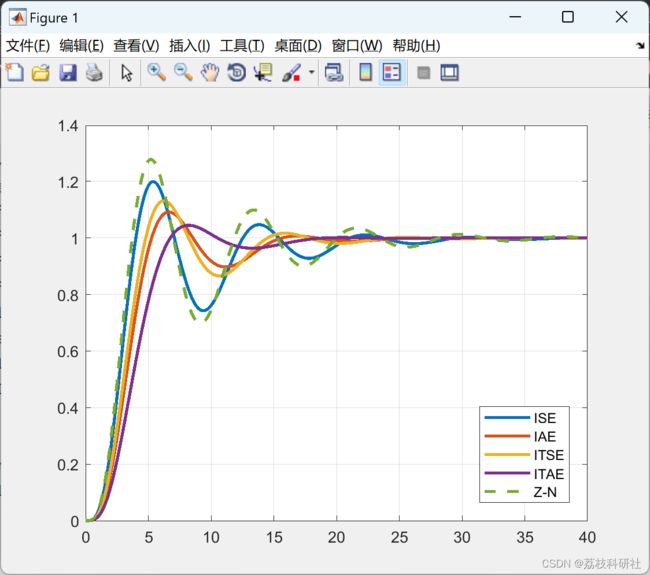
比较采用不同性能指标设计的PID控制器的闭环性能。

G=zpk([],[-3 -2 -1 0],1);   % The plant
C1=optimPID(G,3,1);   % PID-Control, ISE index
C2=optimPID(G,3,2);   % PID-Control, IAE index
C3=optimPID(G,3,3);   % PID-Control, ITSE index
C4=optimPID(G,3,4);   % PID-Control, ITAE index
K=znpidtuning(G,3);   % Ziegler-Nichols stability margin tuning
t=0:0.1:30;
y1=step(feedback(C1*G,1),t); %Closed-loop step response of C1
y2=step(feedback(C2*G,1),t); %Closed-loop step response of C2
y3=step(feedback(C3*G,1),t); %Closed-loop step response of C3
y4=step(feedback(C4*G,1),t); %Closed-loop step response of C4
%Closed-loop step response of K
y=step(feedback(G*(K.kc*(1+tf(1,[K.ti 0])+tf([K.td 0],1))),1),t);
plot(t,y1,t,y2,t,y3,t,y4,t,y,'--','Linewidth',2)
legend('ISE','IAE','ITSE','ITAE','Z-N','Location','Best')
grid

% The comparison shows that the ITSE index leads to the best PID
% controller.

具有重复极点的四阶系统。

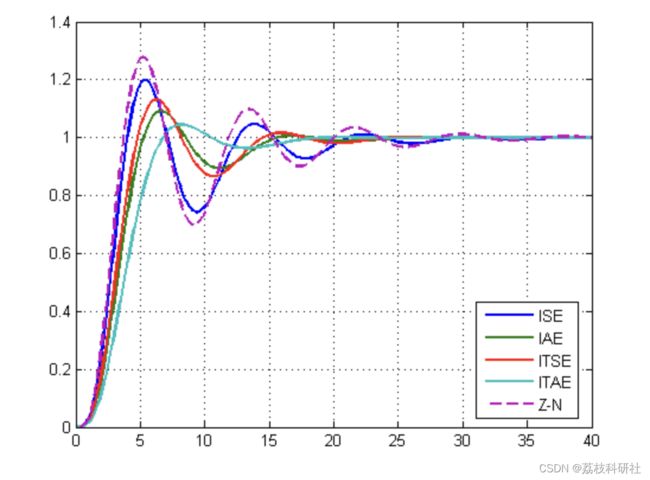
比较PI控制器的闭环性能。

G=tf(1,[1 4 6 4 1]);   % The plant
C1=optimPID(G,2,1);   % PID-Control, ISE index
C2=optimPID(G,2,2);   % PID-Control, IAE index
C3=optimPID(G,2,3);   % PID-Control, ITSE index
C4=optimPID(G,2,4);   % PID-Control, ITAE index
K=znpidtuning(G,2);   % Ziegler-Nichols stability margin tuning
t=0:0.1:40;
y1=step(feedback(C1*G,1),t); %Closed-loop step response of C1
y2=step(feedback(C2*G,1),t); %Closed-loop step response of C2
y3=step(feedback(C3*G,1),t); %Closed-loop step response of C3
y4=step(feedback(C4*G,1),t); %Closed-loop step response of C4
%Closed-loop step response of K
y=step(feedback(G*(K.kc*(1+tf(1,[K.ti 0]))),1),t);
plot(t,y1,t,y2,t,y3,t,y4,t,y,'--','Linewidth',2)
legend('ISE','IAE','ITSE','ITAE','Z-N','Location','Best')
grid

% This time the ITAE index gives the best design.

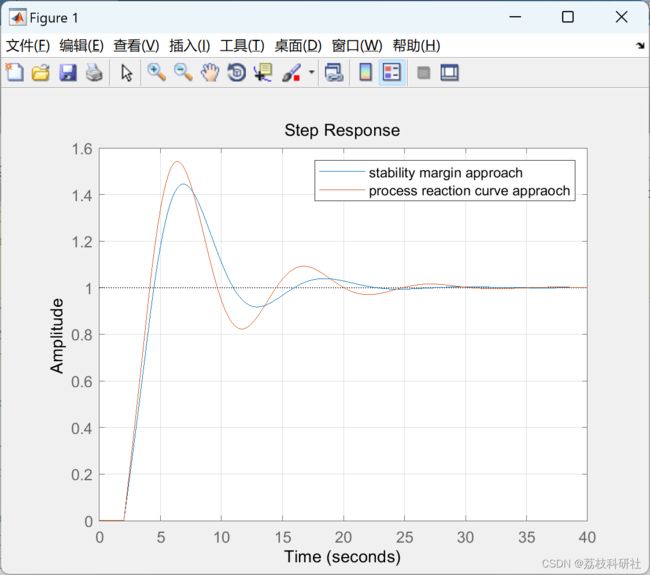
 闭环性能比较

 部分代码：

% first let us get stability margins
[Gm,Pm,Wcg]=margin(g);
% If we increase the gain by the Gm, the system is critically stable. Hence
% the ultimate gain in dB equals to the gain margin, i.e.
% 20 * log10(ku) = Gm, hence:
% ku=10^(Gm/20);
% In Control System Toolbox, the gain margin is shown in dB in the graph,
% but returns in normal ratio.
ku=Gm;
% If we increase the gain by ku, the system will ocsillate at Wcg
% frequency, hence
pu=2*pi/Wcg;
% Controller parameters based on Ziegler-Nichols' tuning rule
switch ctype
    case 1              % P-controller
        k.kc=ku/2;
    case 2              % PI-controller
        k.kc=ku/2.2;
        k.ti=pu/1.2;
    case 3              % PID-controller
        k.kc=ku/1.7;
        k.ti=pu/2;
        k.td=pu/8;
end

3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]宋尚飞,刘轩章,陈宏举,康琦,李宸轩,邓涛,吴海浩,史博会,宫敬.PID控制参数对重力式三相分离器生产工艺的影响[J].石油科学通报,2023,8(02):179-192.

[2]Yi Cao (2023). Learning PID Tuning III: Performance Index Optimization.

4 Matlab代码实现