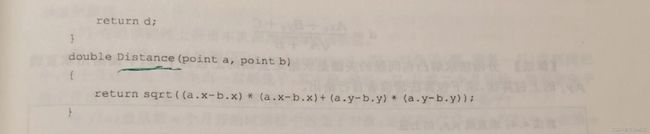「分治法」最近点对距离问题

一、问题描述

给定平面S上n个点，找其中的一对点，使得在n个点组成的 所有点对中，该点对间的距离最小。

假设所讨论的点是以标准笛卡儿坐标形式（x, y）给出的。因 此，在两个点Pi =(xi , yi )和Pj =(xj , yj )之间的距离是标准的欧几里德 距离： d = 根号下( x i − x j ) 2 + ( y i − y j )2

二、问题分析

直接用暴力解法很简单，用结构体把每个点的x、y坐标都存下来之后，用一个二重循环即可获得距离的最大值。但是这样做的时间复杂度也达到了O(n的平方)

那么有没有什么办法，可以把时间复杂度降下来，达到nlogn呢？

思路

首先，利用分治法，将集合S分成两个相等的子集S1、S2。然后在这两个子集中递归的求出距离最近的点对。

这样做，如果最近点对都是分别在两边子集中，那还好说。如果不是分别在两边子集，而是这两个点一个在左边，一个在右边怎么办？这就不是单纯的递归了，子问题并不互斥，存在了overlap的问题。

所以我们把问题划分成两个子集S1、S2之后，出现三种情况：

1. 最近点对的两个点都在S1中
2. 最近点对的两个点都在S2中
3. 最近点对的两个点一个在S1中，一个在S2中

情况1和2可以递归求解，但是3不行。那为了解决情况3，我们应该怎么做呢？

精髓

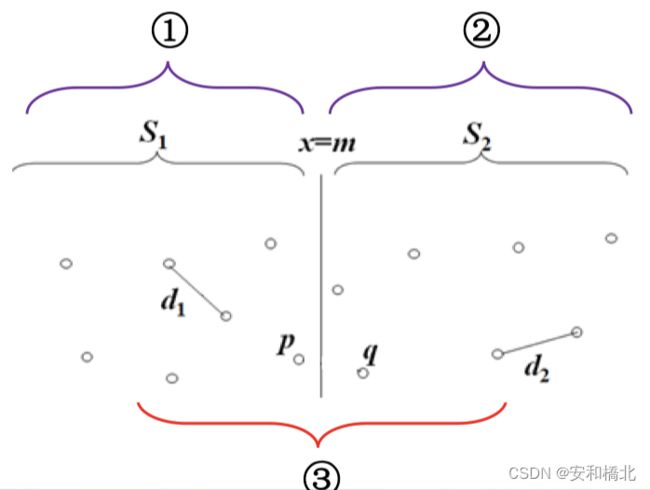
首先我们假设点集S已经按照x坐标升序排列，并且点集S中x坐标的中值就是中间点x的坐标。

我们还是在左边点集S1中和右边点集S2中递归求解，假设S1和S2的最短点对距离分别是d1和d2，然后令d = min { d1, d2 }。

如果说，最后求解出来的S的最短点对距离是小于d的，也就是答案还不在左右两个子集中产生，那么说明这两个点肯定一个在左边点集S1中，一个在右边点集S2中。

这个可以用反证法来证明：

如果不是左右各一个，而是都在一边的话，那么由于这个距离是小于d的，而d又是min { d1, d2 }，所以直接矛盾了，左边点集或者右边点集的最小点对距离肯定不是d1或者d2了。因此得证。

现在我们可以将求解限制在以点集S中线x = m为中心，宽度为2d的垂直地带P1和P2中，垂直带之外的任何点对的距离肯定都大于d。

假设点p(x,y)是集合P1和P2中y坐标最小的点，那么实际上点p可能在P1也可能在P2，但这并不重要。我们现在的目的就是找出在这个垂直地带中，有没有点对的距离比d还小的了。如果存在，那么这个点对就是答案；如果不存在，那么答案就是d。

那么以点p(x,y)为基准，那么我们要找的这个点，肯定是在垂直域[ y , y + d ]这个范围里面。而且在这个范围里面，点的个数不会超过8个！

这又是为什么呢？课堂上老师只是简单的说这可以用鸽笼原理来证明，让同学们自己下去看，接下来我简略解释一下：

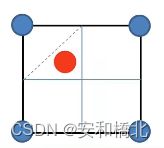
看这个正方形，假设这个是中线x = m右边的这半矩形。为了保证右半边内的点对的距离不小于d（因为如果超过了，那S2点集的最短点对距离就不是d了！），只能把四个点放在四个角。

这时但凡再出现第五个点，那么这个第五个点的距离和另外一个点的距离，肯定是小于d的。也就证明一边最多只有四个点。所以总的来说，在这个矩形内，最多只有8个点。

所以，到目前为止，我们就限定了情况3的可能答案的范围。接下来就可以进行代码书写了。

算法时间复杂度分析

那么在这种情况下，时间复杂度是多少呢？

1. 当点数n为1,2,3的时候，可以不用划分，直接求解即可，这时是O(1)
2. 当点数大于3的时候，就需要划分子问题，进行递归求解。
   递归方程为T(n) = 2T(n/2) + O(n)
   为什么呢？因为划分和合并虽然用的是一个二重循环，但是实际上内层循环的最大值也就是8，所以相当于是O(an)，也就是O(n)。

那么求解递归方程之后即可得出时间复杂度是nlogn。

三、代码

由于本题是书上内容，没有题目和测试用例，所以此处直接附上书上的代码。书上的代码笔者认为写的还是很清晰明了的。