初识决策树(Decision Tree)
今天来看一下西瓜书第四章——决策树。
文章目录
-
-
- 信息增益
- 增益率
- 基尼系数
- 剪枝处理
-
- 预剪枝
- 后剪枝
- 连续值与缺失值处理
-
- 连续值处理
- 缺失值处理
-
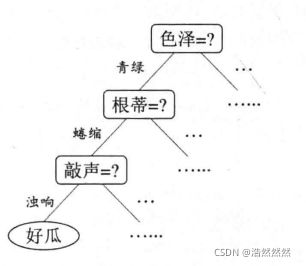
决策树,简单来说就是一个树形结构从根节点往叶子节点进行决策,树内部的每一个节点是对一个特征的测试,树的分支代表该特征的每一个测试结果,而树的每一个叶子节点代表一个类别。
信息增益
信息熵是度量样本纯度的一种指标,假设样本集合 D D D 中第 k k k 类样本所占比例为 p k , k = 1 , 2 , ⋯ , N p_k,k=1,2,\cdots,N pk,k=1,2,⋯,N (在二分类中, N = 2 N=2 N=2),那么 D D D 的信息熵定义为
E n t ( D ) = − ∑ k = 1 N p k l o g 2 p k Ent(D)=-\sum_{k=1}^{N}p_klog_2p_k Ent(D)=−k=1∑Npklog2pk
E n t ( D ) Ent(D) Ent(D) 的值越小,说明 D D D 的纯度越高。
假设某一个特征 a a a 有 V V V 个取值,记为 [ a 1 , ⋯ , a V ] [a^1,\cdots,a^V] [a1,⋯,aV],那么在该特征 a a a 中,第 v v v 个取值 a v a^v av 的所有个数,记为 D v D^v Dv。于是该特征的信息增益为:
G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V D v D E n t ( D v ) Gain(D,a)=Ent(D)-\sum_{v=1}^{V} \frac{D^v}{D}Ent(D^v) Gain(D,a)=Ent(D)−v=1∑VDDvEnt(Dv)
一般来说,信息增益越大,意味着用该特征进行划分获得的纯度提升越大,因此,我们一般选择 m a x ( G a i n ( D , a ) ) max(Gain(D,a)) max(Gain(D,a)) 的特征来进行划分。
注意:
一个特征进行划分后,可能那么会得到多个分支,多个分支也一样递归地计算 G a i n Gain Gain 来进行分支,不同的是,各个分支计算时,需要注意样本数已经变化,即要用该分支的样本计算,直到不可再分为止。
增益率
由信息增益的计算公式可以看出,当特征的取值数量 V V V 较多时,会导致该特征的信息增益大一些,使得决策树会更偏向于该特征进行划分,这是不可取的。
因此, C 4.5 C4.5 C4.5 决策树算法没有直接使用信息增益进行划分,而是用增益率来选择特征划分。
增益率定义如下:
G a i n _ r a t i o ( D , a ) = G a i n ( D , a ) I V ( a ) Gain\_ ratio(D,a)=\frac{Gain(D,a)}{IV(a)} Gain_ratio(D,a)=IV(a)Gain(D,a)
其中 I V ( a ) = − ∑ v = 1 V D v D l o g 2 D v D IV(a)=-\sum_{v=1}^{V}\frac{D^v}{D}log_2\frac{D^v}{D} IV(a)=−∑v=1VDDvlog2DDv
容易看出当 V V V 越大时, I V IV IV 的值越大,增益率就会越小,这意味着增益率更偏向于取值数量较少的特征。
即用信息增益和增益率相结合:
- 先从候选划分特征中找出信息增益高于平均水平的属性;
- 再从中选择增益率最高的特征进行划分。
基尼系数
C A R T CART CART 决策树使用 G i n i Gini Gini 系数来选择特征进行划分,其定义如下:
G i n i ( D ) = ∑ k = 1 N ∑ k ′ ≠ k p k p k ′ = 1 − ∑ k = 1 N p k 2 \begin{aligned} Gini(D)&=\sum_{k=1}^{N}\sum_{k^{'}\ne k} p_kp_{k'}\\ &=1-\sum_{k=1}^{N}p_k^2 \end{aligned} Gini(D)=k=1∑Nk′=k∑pkpk′=1−k=1∑Npk2
简单来说, G i n i ( D ) Gini(D) Gini(D) 反映了从数据集 D D D 中随机抽取两个样本,其类别标记不一致的概率。因此, G i n i ( D ) Gini(D) Gini(D) 越小,则数据集 D D D 的纯度越高。
同样的,某个特征 a a a 的基尼系数定义如下:
G i n i _ i n d e x ( D , a ) = ∑ v = 1 V D v D G i n i ( D v ) Gini\_ index(D,a)=\sum_{v=1}^{V}\frac{D^v}{D}Gini(D^v) Gini_index(D,a)=v=1∑VDDvGini(Dv)
与信息增益不同的是,基尼系数一般选择 m i n ( G i n i _ i n d e x ( D , a ) ) min(Gini\_ index(D,a)) min(Gini_index(D,a)) 的特征来进行划分。
剪枝处理
剪枝是为了防止决策树在学习时过拟合,即泛化能力太差。剪枝一般有预剪枝和后剪枝,下面介绍这两种剪枝方法。
先看一下西瓜书中未剪枝的决策树:
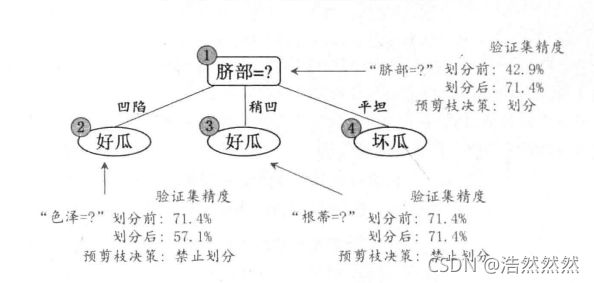
预剪枝
预剪枝是指在决策树生成过程中,对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树泛化性能提升,则停止划分并将当前结点标记为叶结点。
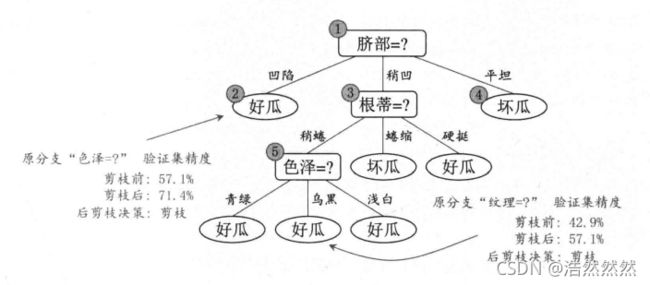
后剪枝
后剪枝则是先从训练集生成一棵完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升,则将该子树替换为叶结点。
连续值与缺失值处理
连续值处理
当某个特征的取值为连续值,说明可取值的数量太多,这不能直接按连续值进行划分,此时,我们需要将连续值离散化,最简单的策略就是采用二分法处理连续值。
给定样本集 D D D 和连续属性 a a a ,假定 a a a 出现了 n n n 个不同的取值,先将这些值从小到大进行排序,记为 [ a 1 , a 2 , ⋯ , a n ] [a^1,a^2,\cdots,a^n] [a1,a2,⋯,an]。基于划分点 t t t 可将 D D D 分为子集
D t − D_t^{-} Dt− 和 D t + D_t^{+} Dt+,其中 D t − D_t^{-} Dt− 是不大于 t t t 的样本,而 D t + D_t^{+} Dt+ 是大于 t t t 的样本。
显然,对相邻的属性取值 a i 和 a i + 1 a_i和a_{i+1} ai和ai+1 来说,在区间 [ a i , a i + 1 ) [a_i,a_{i+1}) [ai,ai+1) 中取任何值所产生的的划分结果都一样。因此,对连续属性 a a a,我们对 n − 1 n-1 n−1 个元素进行选取划分点:
T a = { a i + a i + 1 2 ∣ 1 ≤ i ≤ n − 1 } \begin{aligned} T_{a}= \left \{ \frac {a^i+a^{i+1}}{2} | 1\le i \le n-1 \right \} \end{aligned} Ta={2ai+ai+1∣1≤i≤n−1}
即把区间 [ a i + a i + 1 ) [a^i+a^{i+1}) [ai+ai+1) 的中点作为划分点,那么就可以像离散值一样来考察这些划分点,从而选择最优的划分点进行划分。
同样的,得到信息增益:
G a i n ( D , a ) = m a x t ∈ T a G a i n ( D , a , t ) = m a x t ∈ T a E n t ( D ) − ∑ λ ∈ { − , + } D t λ D E n t ( D t λ ) \begin{aligned} Gain(D,a)&=\underset{t\in T_a}{max}Gain(D,a,t)\\ &= \underset{t\in T_a}{max}Ent(D)-\sum_{\lambda \in \left\{-,+ \right\}}\frac{D_t^\lambda}{D}Ent(D_t^\lambda) \end{aligned} Gain(D,a)=t∈TamaxGain(D,a,t)=t∈TamaxEnt(D)−λ∈{−,+}∑DDtλEnt(Dtλ)
其中, G a i n ( D , a , t ) Gain(D,a,t) Gain(D,a,t) 是 D D D 基于划分点 t t t 二分后的信息增益,我们就可以选择 m a x ( G a i n ( D , a , t ) ) max(Gain(D,a,t)) max(Gain(D,a,t))的划分点。
缺失值处理
对于一些含有缺失值的数据,少量还好,当缺少的数量多的时候,我们不能丢弃这些数据,应该把他们也一起训练起来。
给定样本集 D D D 和属性 a a a,令 D ~ \widetilde{D} D 表示 D D D 中在属性 a a a 上没有缺失值的样本子集。
显然我们可根据 D ~ \widetilde{D} D 来判断属性 a a a 的优劣。假定属性 a a a 可取值 [ a 1 , a 2 , ⋯ , a V ] [a^1,a^2,\cdots,a^V] [a1,a2,⋯,aV],令 D ~ v \widetilde{D}^v D v 在表示 D ~ \widetilde{D} D 中在属性 a a a 上取值为 a v a^v av 的样本子集, D ~ k \widetilde{D}_k D k 表示 D ~ \widetilde{D} D 中属于第 k k k 类样本子集,则显然有 D = ⋃ k = 1 N D ~ k D=\bigcup_{k=1}^{N} \widetilde{D}_k D=⋃k=1ND k、 D = ⋃ v = 1 V D ~ v D=\bigcup_{v=1}^{V} \widetilde{D}^v D=⋃v=1VD v。
现在给每个样本 x x x 赋予权重 w x w_x wx,定义如下:
{ ρ = ∑ x ∈ D ~ w x ∑ x ∈ D w x p ~ k = ∑ x ∈ D ~ k w x ∑ x ∈ D ~ w x r ~ v = ∑ x ∈ D ~ v w x ∑ x ∈ D ~ w x \begin{cases} \rho=\frac{\sum_{x\in \widetilde{D}}w_x}{\sum_{x\in D}w_x}\\\\ \widetilde{p}_k=\frac{\sum_{x\in \widetilde{D}_k}w_x}{\sum_{x\in \widetilde{D}}w_x}\\\\ \widetilde{r}_v=\frac{\sum_{x\in \widetilde{D}^v}w_x}{\sum_{x\in \widetilde{D}}w_x}\\ \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧ρ=∑x∈Dwx∑x∈D wxp k=∑x∈D wx∑x∈D kwxr v=∑x∈D wx∑x∈D vwx
直观地看,对属性 a a a, ρ \rho ρ 表示无缺失值样本所占的比例, p k p_k pk 表示无缺失值样本中第 k k k 类所占的比例, r ~ v \widetilde{r}_v r v 则表示无缺失值样本中在属性 a a a 上取值 a v a^v av 的样本所占的比例。显然, ∑ k = 1 N p ~ k = 1 , ∑ v = 1 V r ~ v = 1 \sum_{k=1}^{N}\widetilde{p}_k=1,\sum_{v=1}^{V}\widetilde{r}_v=1 ∑k=1Np k=1,∑v=1Vr v=1
于是,就可以将信息增益推广如下:
G a i n ( D , a ) = ρ × G a i n ( D ~ , a ) = ρ × ( E n t ( D ~ − ∑ v = 1 V r ~ v E n t ( D ~ v ) ) ) \begin{aligned} Gain(D,a)&=\rho \times Gain(\widetilde{D},a)\\ &=\rho \times (Ent(\widetilde{D}-\sum_{v=1}^{V}\widetilde{r}_vEnt(\widetilde{D}^v))) \end{aligned} Gain(D,a)=ρ×Gain(D ,a)=ρ×(Ent(D −v=1∑Vr vEnt(D v)))
其中 E n t ( D ~ ) = − ∑ k = 1 N p ~ k l o g 2 p ~ k Ent(\widetilde{D})=-\sum_{k=1}^{N}\widetilde{p}_klog_2\widetilde{p}_k Ent(D )=−∑k=1Np klog2p k
若样本 x x x 在划分属性 a a a 上的取值已知,则将 x x x 划入与其取值对应的子结点,且样本权值在子结点中保待为 w x w_x wx。若样本 x x x 在划分属性 a a a 上的取值未知 则将 x x x 同时划入所有子结点,且样本权值在与属性值 a v a^v av 对应的子结点中调整为 r ~ v × w x \widetilde{r}_v\times w_x r v×wx。
参考资料
[1] 周志华.机器学习[M].北京:清华大学出版社,2020.