数据结构与算法(1)——动态规划
数据结构与算法(1)——动态规划
- 1. 动态规划的定义
- 2. 动态规划题目的特点
- 3. 动态规划的解题步骤
-
- 3.1 确定状态
- 3.2 转移方程
- 3.3 初始条件和边界情况
- 3.4 计算顺序
- 4. LeetCode中的动态规划题及案例分析
- 5. LeetCode中的动态规划题
1. 动态规划的定义
动态规划(英语:Dynamic programming,简称DP)是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常常适用于有重叠子问题和最优子结构性质的问题。
重叠子问题:原问题能够拆解为有限个的子问题,且这些子问题有重复出现。如果没有重复的子问题出现,那么和递归相比,动态规划没有优势。
最优子结构:局部最优解能决定全局最优解(对有些问题这个要求并不能完全满足,故有时需要引入一定的近似)。简单地说,问题能够分解成子问题来解决。
动态规划有点类似于数学归纳法,但不完全是,因为动态规划中会出现重复的子问题,但是数学归纳法好像没有重复的子问题这一说法。
2. 动态规划题目的特点
动态规划的题目一定是笼统的数量,不会具体到详细的过程,以下是三种常见的动态规划提问方式:
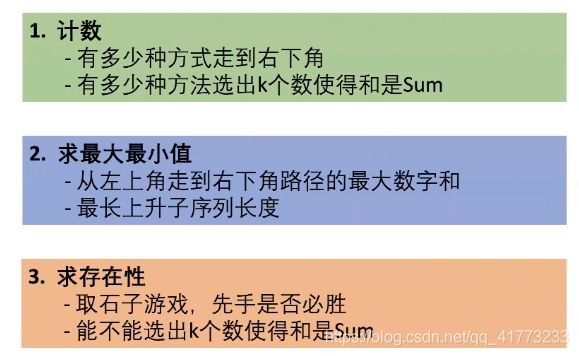
比如求“最长上升子序列长度”可能是动态规划问题,但是求“最长上升子序列的序列值”那就一定不是动态规划问题,因为它详细到具体的序列内容。
3. 动态规划的解题步骤
3.1 确定状态
状态决定了需要维护什么样的数组,是一维数组还是二维数组,数组元素含义是什么。

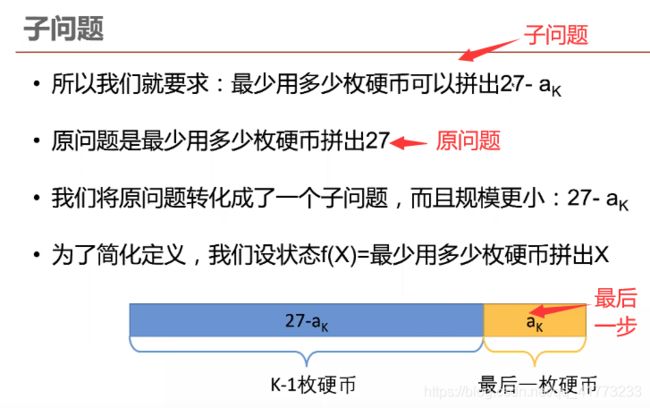
最后一步:指假设前面的所有信息都知道了,只差最后一步即可完成原问题。
子问题:和原问题一样,只是问题规模变小了。
以LeetCode 322. 零钱兑换为例。假设amount=27,然后给了[2,5,7]三种面值的硬币,那么子问题和最后一步如下所示:
一旦搞清楚子问题了(自然也就搞清楚了最后一步),那么就可以找到状态,每个状态值都对应一个待求的子问题,原问题就是最后一个状态值。
因此一般情况下,可以认为,需要求什么,什么就是状态。
3.2 转移方程
根据实际问题,列出转移方程。
转移方程即:求解当前状态值,需要知道哪些状态值?和它们是什么关系?
列出转移方程的重要看问题中的一步操作是什么?注意,只能操作一步。
比如在上面的问题中,转移方程如下:
3.3 初始条件和边界情况
因为动态规划是从题目“末端”开始,往前考虑,因此需要给定初始条件和边界情况,才能够从前往后演算,得到所需结果。
3.4 计算顺序
确定计算顺序的方法很简单,就看自己维护的那个状态数组。在用转移方程计算数组中的状态值时,一定要保证转移方程等号右边的数都算出来了,这样才能算出转移方程左边的状态值。因此通过这种方式来确定计算数组的状态值的顺序。
一般来说,一维数组是从左往右,二维数组是从左往右,从上到下,但还是要具体问题具体分析,就按照刚刚所述的判断依据来。
4. LeetCode中的动态规划题及案例分析
以下是LeetCode动态规划专题链接,对动态规划不熟悉的同学可以按照本文思路,多刷些题:
https://leetcode-cn.com/tag/dynamic-programming/problemset/
下面我再以一道LeetCode困难等级的题为例,讲述本文方法的使用过程。
题目详情请见:72. 编辑距离
首先,确定状态。原问题是 word1 转换成 word2 所使用的最少操作数,所以状态就是“X 转换成 Y 所使用的最少操作数”。确定了状态,我们就知道此题需要维护一个二维数组dp(当然可以优化成只需要维护一个一维数组,这里暂不讲),但数组元素(即状态值)的含义是什么呢?数组的索引都是整数,而不是字符串,所以X,Y不能直接充当数组索引,我们可以用word1的前i个字符串充当X,word2的前j个字符串充当Y,这样就形成了整型到字符串的映射。因此状态值 d p [ i ] [ j ] dp[i][j] dp[i][j]代表 word1的前 i i i个字符串 转换成 word2的前 j j j个字符串 所使用的最少操作数。最后一个状态值即为原问题。
然后,根据实际问题,列出转移方程。因为只允许三个操作:插入一个字符、删除一个字符、替换一个字符,且插入一个字符和删除一个字符是相反操作。 d p [ i ] [ j ] dp[i][j] dp[i][j]和哪些状态值有关呢?这就需要看问题中的一步操作有哪些。对于此问题而言,对A插入字符和对B删除字符等效,对A删除字符和对B插入字符等效,因此只需要考虑删除操作,不需要考虑插入操作。如果word1的前 i − 1 i-1 i−1个字符串 转换成 word2的前 j j j个字符串 所使用的最少操作数为 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j],那么word1的前 i i i个字符串 转换成 word2的前 j j j个字符串 所使用的最少操作数为 d p [ i ] [ j ] = d p [ i − 1 ] [ j ] + 1 dp[i][j]=dp[i-1][j]+1 dp[i][j]=dp[i−1][j]+1,因为只需要对word1进行一步删除,删除word1最后一个字符即可。同理,还可以得到 d p [ i ] [ j ] = d p [ i ] [ j − 1 ] + 1 dp[i][j]=dp[i][j-1]+1 dp[i][j]=dp[i][j−1]+1这个等式。目前我们还没有考虑替换操作。因为替换不会改变字符串的长短,如果word1的前 i − 1 i-1 i−1个字符串 转换成 word2的前 j − 1 j-1 j−1个字符串 所使用的最少操作数为 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1],那么word1的前 i i i个字符串 通过替换操作转换成 word2的前 j j j个字符串 所使用的最少操作数为 d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] + i n t ( w o r d 1 [ i ] ! = w o r d 2 [ j ] ) dp[i][j]=dp[i-1][j-1]+int(word1[i]!=word2[j]) dp[i][j]=dp[i−1][j−1]+int(word1[i]!=word2[j]),这我用一个例子说明一下,假设word1为“abc”,word2为“adc”,因为“ab”到“ad”只需要一步替换即可,所以 d p [ 2 ] [ 2 ] = 1 dp[2][2]=1 dp[2][2]=1,那么 d p [ 3 ] [ 3 ] dp[3][3] dp[3][3]的值取决于word1的第3个字符和word2的第3个字符是否相等,如果相等,则不需要任何操作,如果不等,就需要替换操作,这就是方程后面的int项的来源。注意:为什么我们总是在单词 X 和 Y 的末尾插入或者修改字符,能不能在其它的地方进行操作呢?答案是可以的,但是我们知道,操作的顺序是不影响最终的结果的。例如对于单词 cat,我们希望在 c 和 a 之间添加字符 d 并且将字符 t 修改为字符 b,那么这两个操作无论为什么顺序,都会得到最终的结果 cdab,也就是我们在“c”的时候就插入“d”,变成“cd”,而不是等到“cab”的时候再插入“d”
综上,转移方程为:
d p [ i ] [ j ] = m i n { d p [ i − 1 ] [ j ] + 1 , d p [ i ] [ j − 1 ] + 1 , d p [ i − 1 ] [ j − 1 ] + i n t ( w o r d 1 [ i ] ! = w o r d 2 [ j ] ) } dp[i][j] = min\{ dp[i-1][j]+1, dp[i][j-1]+1, dp[i-1][j-1]+int(word1[i]!=word2[j]) \} dp[i][j]=min{dp[i−1][j]+1,dp[i][j−1]+1,dp[i−1][j−1]+int(word1[i]!=word2[j])}
接着,确定初始条件和边界情况,显然这个矩阵的初始条件是行列索引为0的情况,那么令 d p [ 0 ] [ j ] = j dp[0][j]=j dp[0][j]=j, d p [ i ] [ 0 ] = i dp[i][0]=i dp[i][0]=i,即不断插入字符(或者从后往前看就是不断删除字符)。
最后确定计算顺序。如下图所示,在算绿色格子之前,需要知道红色格子的值,因此此二维数组的计算顺序可以为一列列计算,也可以为一行行计算。
本题的官方python代码如下:
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
n = len(word1)
m = len(word2)
# 有一个字符串为空串
if n * m == 0:
return n + m
# DP 数组
D = [ [0] * (m + 1) for _ in range(n + 1)]
# 边界状态初始化
for i in range(n + 1):
D[i][0] = i
for j in range(m + 1):
D[0][j] = j
# 计算所有 DP 值
for i in range(1, n + 1):
for j in range(1, m + 1):
left = D[i - 1][j] + 1
down = D[i][j - 1] + 1
left_down = D[i - 1][j - 1]
if word1[i - 1] != word2[j - 1]:
left_down += 1
D[i][j] = min(left, down, left_down)
return D[n][m]
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/edit-distance/solution/bian-ji-ju-chi-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
参考资料:
本文部分参考了B站视频:【动态规划专题班】ACM总冠军、清华+斯坦福大神带你入门动态规划算法
5. LeetCode中的动态规划题
70. 爬楼梯
简评:简单的动态规划题,可以考虑只使用常数项的时间复杂度来完成此题,即在动态规划中,只使用两个变量。
198. 打家劫舍
简评:简单的动态规划题,可以考虑只使用常数项的时间复杂度来完成此题,即在动态规划中,只使用三个变量。
413. 等差数列划分
简评:此题我写的时候并没有把它想成动态规划的题,只是单纯地比较差值数组中相邻两项是否相等,然后用一个变量res进行计数,直接计算所有满足要求的子数组个数。看评论发现有些人将其理解为动态规划题,也是可以的。
64. 最小路径和
简评:简单的二维动态规划,应该熟练掌握如何优化空间复杂度,将其降为1维的空间复杂度。
221. 最大正方形
简评:二维动态规划,此题的状态转移方程比较难想出来,而且由于这个状态转移方程的特点,无法将2维动态规划转为1维动态规划。
279. 完全平方数
简评:类似于下面的“322. 零钱兑换”的题目,但是要注意的是,尽量避免开方运算,因为它会带来较大的时间复杂度。想办法避免开方!
91. 解码方法
简评:此题的主要难点在于理解题意,搞明白这个动态规划和爬楼梯差不多,只是需要加一些判定条件而已。以及注意边界条件的赋值。
139. 单词拆分
简评:将题目中所说的wordDict转换为哈希表,key是字符长度,value是一个集合set,set中装的是字符。然后把此问题转换为“322. 零钱兑换”的问题。
416. 分割等和子集
简评:二维动态规划,此题的状态转移方程比较难想出来,而且很难联想到这是一个01背包的问题,应该熟练掌握如何优化空间复杂度,将其降为1维的空间复杂度。
322. 零钱兑换
简评:可以看做完全背包问题。