高等数学下——平面与直线
目录
- 题目
- 解答
- 知识点(平面与直线方程)
-
- 一、平面方程的各种形式
-
- 1. 平面的点法式方程
- 2. 平面的一般方程
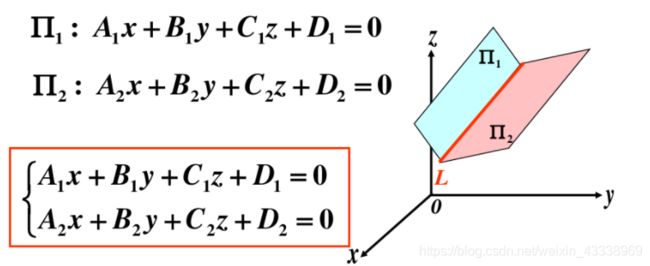
- 二、直线方程的各种形式
-
- 1. 空间直线的一般方程
- 三、平面直线间的夹角及相互关系
题目
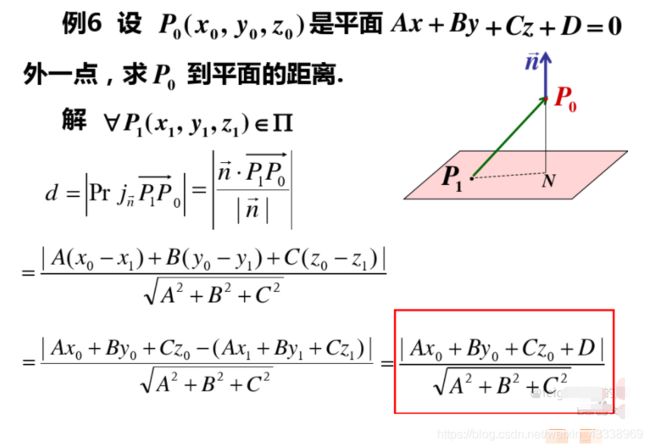
设平面 П: x − 4 y + 2 z + 9 = 0 П :x- 4y+2z+9=0 П:x−4y+2z+9=0,直线L: { 2 x − 2 y + z + 9 = 0 x − 2 y + 2 z + 11 = 0 \left\{\begin{matrix}2x-2y+z+9=0\\x-2y+2z+11=0\end{matrix}\right. {2x−2y+z+9=0x−2y+2z+11=0,求在平面 П П П上,通过直线L与平面 П П П 的交点,且与直线L垂直的直线方程。
解答
∵ { 2 x − 2 y + z + 9 = 0 x − 2 y + 2 z + 11 = 0 \because\left\{\begin{array}{l} 2 x-2 y+z+9=0 \\ x-2 y+2 z+11=0 \end{array}\right. ∵{2x−2y+z+9=0x−2y+2z+11=0
∴ x − z − 2 = 0 ( 1 ) \therefore x-z-2=0 (1) ∴x−z−2=0(1)
即: x = z + 2 即:x=z+2 即:x=z+2
2 x − 3 z − 13 = 0 ( 2 ) 即: y = 13 + 3 z 2 \begin{aligned} 2 x-3 z-13 &=0(2) \\ 即:y &=\frac{13+3 z}{2} \end{aligned} 2x−3z−13即:y=0(2)=213+3z
代入平面 П: x − 4 y + 2 z + 9 = 0 П:x-4y+2z+9=0 П:x−4y+2z+9=0得:
2 + z − 2 ( 13 + 3 z ) + 2 z + 9 = 0 z = − 5 \begin{array}{r} 2+z-2(13+3 z)+2 z+9=0 \\ z=-5 \end{array} 2+z−2(13+3z)+2z+9=0z=−5
可得, { x = − 3 y = − 1 \left\{\begin{array}{l} x=-3 \\ y=-1 \end{array}\right. {x=−3y=−1
即:直线 L 与平面 П П П交点为 ( − 3 , − 1 , − 5 ) (-3,-1,-5) (−3,−1,−5)
设:直线L的方向向量为 s → \overrightarrow{s} s
s ⃗ = n 1 → × n 2 → = ∣ i ⃗ j ⃗ k ⃗ 2 − 2 1 1 − 2 2 ∣ = − { 2 , 3 , 2 } \vec{s}=\overrightarrow{n_{1}} \times \overrightarrow{n_{2}}=\left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ 2 & -2 & 1 \\ 1 & -2 & 2 \end{array}\right|=-\{2,3,2\} s=n1×n2= i21j−2−2k12 =−{2,3,2}
易知: − 2 ( − 3 − x ) − 3 ( − 1 − y ) − 2 ( − 5 − z ) = 0 -2(-3-x)-3(-1-y)-2(-5-z)=0 −2(−3−x)−3(−1−y)−2(−5−z)=0
即, 2 x + 3 y + 2 z + 19 = 0 2x+3y+2z+19=0 2x+3y+2z+19=0
故,直线方程为: { x − 4 y + 2 z + 9 = 0 2 x + 3 y + 2 z + 19 = 0 \left\{\begin{array}{c} x-4 y+2 z+9=0 \\ 2 x+3 y+2 z+19=0 \end{array}\right. {x−4y+2z+9=02x+3y+2z+19=0
知识点(平面与直线方程)
一、平面方程的各种形式
1. 平面的点法式方程
如果一非零向量垂直于一平面,这向量就叫做该平面的法向量.
已知平面的法向量为 n ⃗ = { A , B , C } , 且过点 M 0 ( x 0 , y 0 , z 0 ) , 设平面上的任一点为 M ( x , y , z ) 必有 \begin{aligned} &\text { 已知平面的法向量为 } \vec{n}=\{A, B, C\}, \text { 且过点 } M_{0}\left(x_{0}, y_{0}, z_{0}\right),\\&\text { 设平面上的任一点为 } M(x, y, z) \text { 必有 } \end{aligned} 已知平面的法向量为 n={A,B,C}, 且过点 M0(x0,y0,z0), 设平面上的任一点为 M(x,y,z) 必有
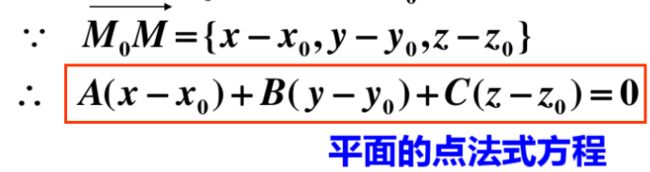
例1 、求过三点 A ( 2 , − 1 , 4 ) , B ( − 1 , 3 , − 2 ) 和 C ( 0 , 2 , 3 ) A(2,-1,4) ,B(-1,3,-2) 和 C(0,2,3) A(2,−1,4),B(−1,3,−2)和C(0,2,3)的平面方程。
解: A B → = { − 3 , 4 , − 6 } , A C → = { − 2 , 3 , − 1 } \quad \overrightarrow{A B}=\{-3,4,-6\} , \quad\overrightarrow{A C}=\{-2,3,-1\} AB={−3,4,−6},AC={−2,3,−1}
取: n ⃗ = A B → × A C → = { 14 , 9 , − 1 } \vec{n}=\overrightarrow{A B} \times \overrightarrow{A C}=\{14,9,-1\} n=AB×AC={14,9,−1}
所求平面方程为:
14 ( x − 2 ) + 9 ( y + 1 ) − ( z − 4 ) = 0 14(x-2)+9(y+1)-(z-4)=0 14(x−2)+9(y+1)−(z−4)=0
化简得: 14 x + 9 y − z − 15 = 0 14 x+9 y-z-15=0 14x+9y−z−15=0
2. 平面的一般方程
由平面的点法式方程
A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 ⇒ A x + B y + C z − ( A x 0 + B y 0 + C z 0 ) = 0 令: − ( A x 0 + B y 0 + C z 0 ) = D 故: A x + B y + C z + D = 0 \begin{array}{c} A\left(x-x_{0}\right)+B\left(y-y_{0}\right)+C\left(z-z_{0}\right)=0 \\ \Rightarrow A x+B y+C z-\left(A x_{0}+B y_{0}+C z_{0}\right)=0 \\ \\ 令:-\left(A x_{0}+B y_{0}+C z_{0}\right)=\boldsymbol D \\ 故:\qquad A x+B y+C z+D=0 \end{array} A(x−x0)+B(y−y0)+C(z−z0)=0⇒Ax+By+Cz−(Ax0+By0+Cz0)=0令:−(Ax0+By0+Cz0)=D故:Ax+By+Cz+D=0
法向量 n ⃗ = { A , B , C } \vec{\boldsymbol n}=\{A, B, C\} n={A,B,C} .
平面一般方程的几种特殊情况:
- D = 0 \boldsymbol D=0 D=0, 平面通过坐标原点 ;
- A = 0 , { D ≠ 0 平面平行于 x 轴 D = 0 平面通过 x 轴 \boldsymbol A=0,\left\{\begin{array}{ll}D \neq 0 & \text { 平面平行于}\boldsymbol x\text { 轴 } \\ D=0 & \text { 平面通过 } \boldsymbol x\text { 轴 } \end{array}\right. A=0,{D=0D=0 平面平行于x 轴 平面通过 x 轴
类似地可讨论 B = 0 , C = 0 \quad {B}={0}, C=0 B=0,C=0- A = B = 0 , { D ≠ 0 平面平行于 x o y 坐标面 D = 0 x o y 坐标面 ; \mathbf{A=B=0},\left\{\begin{array}{l}D \neq 0 \quad \text { 平面平行于}\mathbf{xoy}{坐标面 } \\ D=0 \quad\mathbf{xoy}\text {坐标面 } ;\end{array}\right. A=B=0,{D=0 平面平行于xoy坐标面D=0xoy坐标面 ;
类似地可讨论 A = C = 0 , B = 0 A=C=0, B =0 \quad A=C=0,B=0情形