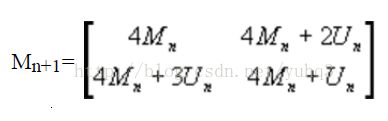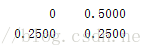关于图像抖动实验
一、背景介绍
在过去十年的计算机发展历史中,我们常常使用的是R、G、B各8位的24位真彩色图像。但如果要求将这种图像在色彩空间有限的显示屏上显示出来,或在打印机上打印出来,往往因为它们的低分辨率使得一张清晰的图像在显示出来之后变得模糊或者失真,因此就需要半色调技术来帮助我们最大程度地还原真实图像。
半色调技术,是通过色点大小或密度的变化造成总体强度的变化,从而表现出较多的对比度,达到了使用较少的色彩模拟表达较多色调的目的。[1]随着半色调算法的发展,如今大多数算法可分为两种:以Bayer抖动为代表的规则抖动算法、以Floyd Steinberg为代表的误差分散算法,两者各有优缺好坏,往往根据不同的图像显示需求来选择相应的算法。尽管有了这几种代表性算法,后人也一直在此基础上不断改良,添砖加瓦,锦上添花。
二、回顾算法
第一种算法“Bayer抖动”[2]:
由Limb在1969年提出,其标准图案算法的递推公式为:
图2.1
其中,Mn代表当前图案矩阵,Un代表当前图案矩阵大小的单位矩阵,Mn+1代表下一个图案矩阵。
所谓标准图案指的是一个整数矩阵,其中每个值包括从0到255.构造这样的标准图案是为了节省256个灰度级别所要占用的二值点阵空间。然后通过以上递推公式可以得到想得到的矩阵大小表示。但值得注意的是,当一个原图为M*N*B bit的灰度图通过Bayer抖动得到m*n的图案表示后,无法再从m*n的图案表示逆转回去,因为不知道原图的(x,y)对应图案表示的哪一点,类似图像处理的上采样与下采样。
这种规则抖动的优点是算法简单,但缺点是图案化比较明显。另外,它对图像的处理也不理想,因为标准图案点的灰度值与图案点的灰度值相差无论大还是小,只要超过阈值(判断是否大于标准灰度值)就赋予白色或黑色的属性,这样的误差可能是比较大的。
第二种算法”Floyd-Steinberg“[2]:
针对Bayer算法的缺点,Floyd-Steinberg算法将图案与标准图案之间的误差传播到附近的点,也即误差扩散,就是色彩深度降低时,将点变化的误差扩散,使得肉眼在观察图片时相邻点之间的误差就会变小。例如原图某像素与对应灰度级别之间误差值为e,其邻居像素可能加上1/8*e后再变换,如此叠加,整体视觉效果就不会太突兀。
虽然这种算法有效改善了图像图案化的缺陷,但当颜色特别丰富的图像需要转换成低彩色时,Floyd算法仍然不能解决过多低位丢失的问题。
第三种算法“改进的动态Bayer抖动算法”[3]:
对于4X4 的Bayer抖动矩阵来说,当其被置于一帧图像中处理时,该抖动矩阵具有轮换性,即对于连续不同的帧中处于相同位置的4X4像素块,套用轮转的抖动矩阵,会出现不同的抖动图案,但其灰度是一样的。(经过一周期,明暗交替的像素块灰度总和不变)通过这种方式,可以较好地消除图像阶梯状条纹和达到图像色彩增强的效果。
第四种算法“流行色算法”[4]:
对彩色图像中所有彩色出现的次数进行统计分析,创建一个用于表示颜色和颜色出现频率的统计直方图数组,然后对该直方图数组进行排序,取出现次数最多的前256种颜色作为调色板的颜色,然后原图中剩下的其他颜色按最小邻近规则映射到相应颜色上。这种算法的好处是简单,对颜色种类少的图片有效,但当颜色种类较多,或者图像有高亮斑点出现时,就会产生各种丢失。
第五种算法“八叉树算法”[4]:
将图像中使用的RGB颜色值分布到层状的八叉树中。八叉树深度可达9层,即根节点加上分别表示R、G、B值的每一位八层节点。较低节点层对应出现较少的RGB值。其优点是节省内存并且效率较高。
三、一种灰度图像抖动方法和一种彩色图像抖动方法:
灰色图像抖动方法“Bayer抖动”:
正如上节提到的,Bayer抖动的初始图案矩阵定义为一个2X2的矩阵M1:
图3.1
根据图2.1递推公式,可得矩阵M2:
图3.2
以此类推,我们可以得到M3,M4,…Mn矩阵,然而当矩阵越来越大,则说明一个大小为rows*cols的原图经过打印后将变成大小为(n*rows)*(n*cols)的图案,无法保持原图的大小。为了解决这个问题,我们可以将M3矩阵作为Bayer抖动表,假设原图有256个灰度级,则将(x,y)的灰度级右移两位,即忽略细节层灰度值,此时灰度级为64级,然后对(x,y)分别取模8,得到的新坐标与抖动表,即8X8的M3矩阵作对比,如果当前坐标比抖动表大则赋255(白色),如果比抖动表小则赋0(黑色)。通过这种做法既避免了选点和划分过大的问题,也不会过于失真。
彩色图像抖动方法“Floyd-steinberg”:
如上节所述,当打印彩色图像,能提供的颜色深度较少时,我们可以使用误差传递的方式来弥补颜色深度的缺失。常用的误差传递模板矩阵有:
图3.3 图3.4
及等等更大的误差模板矩阵,这里我们使用的是图3.4的模板。这个误差传递模板的意思是同时对于当前原图坐标(x,y)像素的R、G、B三个通道,即对应这个矩阵的左上角,若在打印过程中存在误差,即原图与打印图像因颜色深度造成的像素值不同,则将这个误差乘以对应模板的数值加到自身、右、下、右下像素中,遍历完整个图像即可输出图像。值得注意的是,这只是从左到右扫描的误差模板,从上往下扫描时,每遍历完一行都需要逆转方向扫描,这样可以减轻图像图案化的视觉效果,逆转扫描时即将第一行两参数对调即可。
四、关键代码:
“Bayer抖动”:
首先初始化图案矩阵m1,然后不断使用递推公式生成m2,m3,m4图案矩阵。
m1 = [[0 2];[3 1]];
u1=ones(2, 2);
m2=[[4*m14*m1+2*u1];[4*m1+3*u1 4*m1+u1]];
u2=ones(4, 4);
m3=[[4*m2 4*m2+2*u2];[4*m2+3*u2 4*m2+u2]];
u3=ones(8,8);
m4=[[4*m3 4*m3+2*u3];[4*m3+3*u3 4*m3+u3]];
遍历整个图像,对每一个像素进行与图案矩阵m3,m4的比较
% bitand 按位做与运算,m3,m4
if (gI(i,j) /4> m4(bitand(i,15) +1, bitand(j,15) +1)) bw(i,j)=255;
else bw(i,j)=0;
“Floyd-Steinberg”:
根据可使用的颜色深度得到当前点的像素值,并计算与原点的误差。
%fix向靠近0取整
val = red_level * fix(img(i,j,1) /red_level);
red_error = img(i, j, 1) - val;
img(i, j,1) =val;
val = green_level * fix(img(i,j,2) /green_level);
green_error = img(i, j, 2) - val;
img(i, j,2) =val;
val = blue_level * fix(img(i,j,3) /blue_level);
blue_error = img(i, j, 3) - val;
img(i, j,3) =val;
当存在误差时,将该误差以误差传递模板的值传递给周围3个像素点。
%判断是否越界%计算误差对右侧的像素的传递
if ((j +1)<= w)
img(i, j +1,1) = img(i,j +1, 1) + red_error *3 / 8;
img(i, j +1,2) = img(i,j +1, 2) + green_error *3 / 8;
img(i, j +1,3) = img(i,j +1, 3) + blue_error *3 / 8;
end
%计算误差对下侧的像素传递
if ((i +1)<= h)
img(i + 1,j,1) = img(i +1,j, 1) + red_error *3 / 8;
img(i + 1,j,2) = img(i +1,j, 2) + green_error *3 / 8;
img(i + 1,j,3) = img(i +1,j, 3) + blue_error *3 / 8;
end
%计算误差对右下侧的像素传递
if ((i +1)<= h && (j +1) <= w)
img(i + 1,j +1, 1) =img(i +1, j + 1,1) +red_error / 4;
img(i + 1,j +1, 2) =img(i +1, j + 1,2) +green_error / 4;
img(i + 1,j +1, 3) =img(i +1, j + 1,3) +blue_error / 4;
end
如果从右往左扫描则相应地由(i+1,j+1)变为(i-1,j-1)。
五、实验结果:
“Bayer抖动”:
图5.1 原图
图5.2 使用M4矩阵的Bayer抖动算法
图5.3 使用M3矩阵的Bayer抖动算法
“Floyd-Steinberg”:
图5.4 原图
图5.5 使用量化级别为32种的Floyd-Steinberg
图5.5 使用量化级别为4种的Floyd-Steinberg
六、总结:
由实验结果可以看到,对于Bayer抖动算法而言,使用M3矩阵得到的结果比较接近原图,而M4矩阵则比原图更黑,更暗,这是因为使用不同大小的矩阵得到的灰度值密度不一样,越大的矩阵就会越密,越不能显示出“白”的部分。而且Bayer抖动算法还是能看到比较明显的规律性图案化的块,所以该算法还有待改善。
对于Floyd-Steinberg算法,在量化级别即可使用的颜色深度与原图差距在一定程度内,这种误差传递算法效果还是比较好的,以肉眼分辨结果图像与原图几乎没有太大差别,只有将它们都放大到比较小的矩阵时,才能看出两者每个像素点其实是有微小的色彩的差异的。而如果当可使用的颜色深度小于一定值时则可以清楚地看到两者的差别:结果图像中有许多像雪花一样的像素块,因为原本图像中丰富的细节已经不能使用贫瘠的颜色深度表达出来了。所以虽然误差传递算法能较好地表达出原图,但在比较苛刻的条件下它也是会有明显的视觉影响。
参考文献
[1] 何志强. 图像抖动技术的原理及实现[J]. 计算机系统应用, 1999,8(7):43-46.
[2]抖动算法小议1 ——coolbacon
http://blog.csdn.net/coolbacon/article/details/4041988
[3] 刘政林, 郭旭, 邹雪城,等. 基于改进Bayer抖动算法的图像色彩增强技术[J]. 华中科技大学学报(自然科学版), 2006,34(5):68-70.
[4]抖动算法小议3——coolbacon
http://blog.csdn.net/coolbacon/article/details/4042122