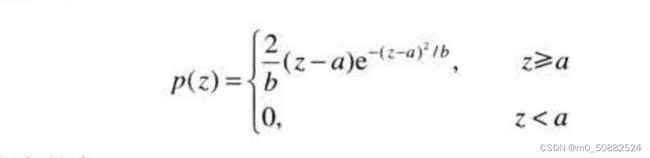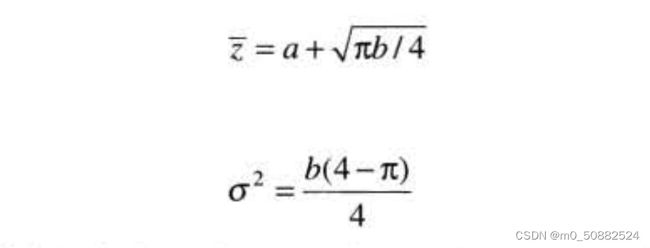数字图像处理 第五章图像复原与重建

数字图像处理 第五章 图像复原与重建

引言

正像图像增强那样，图像复原技术的主要目的是以预先确定的目标来改善图像。尽管两者有相覆盖的领域，但图像增强主要是主观过程，而图像复原则大部分是一个客观过程图像复原试图利用退化现象的某种先验知识来复原被退化的图像。所以复原技术是面对退化模型的，并且采用相反的过程来进行处理，以此来恢复出原图像。

5.1背景知识

本章中给出的教材严格地说只是介绍性的 我们仅从给出的一幅退化数字图像的特点来考虑复原问题，因此对传感器 数字化转换器和显示退化等话题考虑得较少。下面简单介绍下，图像退化、图像在增强、图像复原。
图像退化是图像在形成、记录、处理的过程中，因为各种原因，导致图像质量的下降。图像增强正如第三章介绍的那样是个主观的过程，目的是提高图像质量，提高可懂度，更偏向于主观判断。图像复原是图像退化的反变换，根据图像畸变或退化的原因，进行模型化处理，将质量退化的图像重建或恢复到原始图像，简单的来说就是恢复出图像退化之前的图像。

5.2图像退化与复原

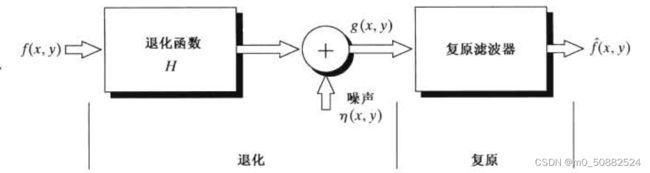
就像这个流程图一样来说明图像退化与图像复原之间的关联。其中，f(x, y)表示输入图像，退化后的图像用g(x, y)表示，退化过程可以分为退化函数H以及加载在图像上的噪声η(x, y)表示，经过复原滤波器后便能得到复原后的图像。
我们可以根据流程图得出退化图像在空间域的表达式

g(x, y) = h（x，y）*f(x，y）＋n（x，y）

以及在频率域的表达式

G(u,v)=H(u,v)F(u,v)+N(u,v)

5.3噪声模型

在图像预处理中，图像去噪是一个很重要的步骤，这个步骤会对后面的结果有很大的影响。因此需要选择适当的滤波技术来增强图像。图像噪声是图像信息或者像素亮度的随机变化。它是由一些因素造成的图像信号的退化。图像

高斯噪声

高斯噪声是指它的概率密度函数服从高斯分布（即正态分布）的一类噪声。
高斯随机变量z的概率密度函数如下所示

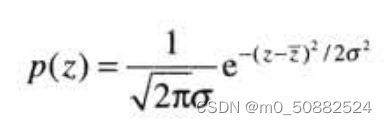
其中μ表示噪声x均值或期望值，σ表示噪声x的标准差

下面是可以实现加入高斯噪声之后的图像的代码实现部分

def gaosi_noise(image, mean=0, var=0.001):
    image = np.array(image/255,dtype=float)
    noise = np.random.normal(mean, var ** 0.5, image.shape)#正态分布
    result = image + noise
    if result.min() < 0:
        clip = -1
    else:
        clip = 0
    result = np.clip(result, clip, 1.0)
    result = np.uint8(result * 255)
    return result
 

椒盐噪声

椒盐噪声也称泊松噪声。，一般是由图像传感器、传输信道及解码处理等产生的黑白相见的亮暗点噪声，椒盐噪声常由图像切割产生。椒盐噪声一般是指两种噪声，即黑噪声和白噪声。
椒盐噪声的概率密度函数如下所示

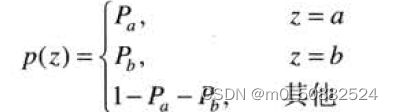
def jiaoyan_noise(image, pera):
    result = np.zeros(image.shape,np.uint8)
    perb = 1 - pera
    for i in range(image.shape[0]):
        for j in range(image.shape[1]):
            rod = random.random()
            if rod < pera:
                result[i][j] = 0
            elif rod > perb:
                result[i][j] = 255
            else:
                result[i][j] = image[i][j]
    return result
 

瑞丽噪声

瑞利噪声的概率密度函数如下所示：

其均值和方差为：

下面是实现在图像中加入瑞利噪声之后图像的代码实现部分

    image = np.array(image, dtype=float)
    noise = np.random.rayleigh(a, size=image.shape)
    result = image + noise
    result = np.uint8(normalize(result) * 255)
    return result

伽马噪声

伽马噪声的概率密度函数为：

下面是实现加入伽马噪声图像之后的代码实现部分：

def gama_noise(image,scale):
    image = np.array(image, dtype=float)
    noise = np.random.gamma(shape=1, scale=scale, size=image.shape)
    result = image+noise
    result = np.uint8(normalize(result) * 255)
    return result

通过输出比较原图与加入高斯噪声、加入椒盐噪声、加入瑞利噪声、加入伽马噪声的五幅图像来作出比较

5.4只存在噪声的复原——空间滤波

当一幅图像中唯一存在的退化是噪声时，空间域表达式为

g(x, y) = f(x，y）＋n（x，y）

频率域表达式为

G(u,v)=F(u,v)+N(u,v)
噪声项是未知的，故从g和G中减去它们不是一个现实的选择。当且仅当存在加性噪声的时候，可以选择空间滤波的方法。

均值滤波

均值滤波的种类有很多种，其中就有算数均值滤波，算术均值滤波是最简单的滤波器。最简单的均值滤波器，在S定义的区域中计算被污染图像g(x,y)的平均值：

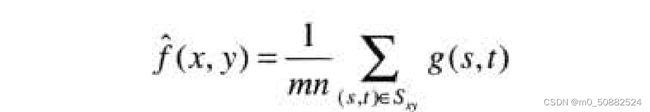
几何均值滤波器，使用几何均值滤波器复原的一幅图像由如下表达式给出

这种处理，几何均值滤波器实现的平滑可以与算数均值滤波相比，但这种处理丢失的图像细节更少。
谐波均值滤波器复原的图像如下

谐波均值滤波器对于盐粒噪声效果较好，但不适用于胡椒噪声。它善于处理像高斯噪声那样的其他噪声。

添加噪声的方式上面有，这里均值滤波器调用OpenCV代码如下，其中cv2.blur的参数为原图像

# 分别实现滤波
# 使用7×7的滤波器
img_mean = cv2.blur(img, (7, 7))
gaussian_mean = cv2.blur(out1, (7,7))
salt_pepper_mean = cv2.blur(out2, (7,7))

逆谐波均值滤波器

其中Q称为滤波器的阶数。这种滤波器适合减少或在实际中消除椒盐噪声的影响。当Q值为正时，该滤波器消除胡椒噪声；当Q值为负时，该滤波器消除盐粒噪声。但它不能同时消除这两种噪声。注意，当Q=0时，逆谐波均值滤波器简化为算术均值滤波器；而当Q=-1时，则为谐波均值滤波器。

统计排序滤波

统计排序滤波器是空间域滤波器，空间域滤波器的响应基于由该滤波器包围图像区域中的像素值的顺序。排序结果决定滤波器的响应。

中值滤波：

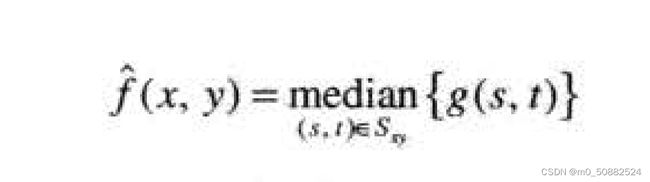
统计学中的排列本身还有很多其他的可能性，可以使用序列中最后一个数值，称为最大值滤波器：

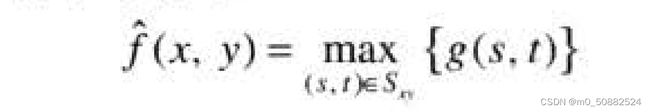
当然还会有最小值滤波器

最小值滤波器对于发现图像中的最暗点非常有用，可以降低盐粒噪声。

自适应滤波

自适应滤波器的行为变化基于由m×n矩形窗口Sxy定义的区域内图像的统计特性，它的性能要明显优于前面介绍的滤波器，代价是滤波器的复杂度。滤波器作用于局部区域Sxy，滤波器在中心化区域中任何点(x,y)上的滤波器响应基于以下4个量，1是g(x, y)表示噪声图像在点(x, y)上的值，2是干扰f(x, y)以形成g(x, y)的噪声方差，3是在Sxy上像素点的局部均值，4是在Sxy上像素点的局部方差。