解剖学关键点检测方向论文翻译和精读:基于热力图回归的CNN融入空间配置实现关键点定位
解剖学关键点检测方向论文翻译和精读:Integrating spatial configuration into heatmap regression based CNNs for landmark localization
Abstract: In many medical image analysis applications, only a limited amount of training data is available due to the costs of image acquisition and the large manual annotation effort required from experts. Training recent state-of-the-art machine learning methods like convolutional neural networks (CNNs) from small datasets is a challenging task. In this work on anatomical landmark localization, we propose a CNN architecture that learns to split the localization task into two simpler sub-problems, reducing the overall need for large training datasets. Our fully convolutional SpatialConfiguration-Net (SCN) learns this simplification due to multiplying the heatmap predictions of its two components and by training the network in an end-to-end manner. Thus, the SCN dedicates one component to locally accurate but ambiguous candidate predictions, while the other component improves robustness to ambiguities by incorporating the spatial configuration of landmarks. In our extensive experimental evaluation, we show that the proposed SCN outperforms related methods in terms of landmark localization error on a variety of size-limited 2D and 3D landmark localization datasets, i.e., hand radiographs, lateral cephalograms, hand MRIs, and spine CTs.
摘要:在许多医学图像分析应用中,由于图像获取的代价高和需要专家的大量手工标注,只有有限的训练数据是可用的。在小数据集上训练近年来最先进的机器学习方法,如卷积神经网络(CNN)是一项具有挑战性的任务。在这项关于解剖学关键点检测的工作中,我们提出了一个CNN架构,它可以学习将定位任务分成两个更简单的子问题,从而减少对大型训练数据集的总体需求。我们的全卷积空间配置网络(SCN)通过乘以其两个组件的热力图预测并以端到端方式训练网络来学习这种简化。因此,SCN将一个组件用于局部准确但模糊的候选预测,而另一个组件通过纳入关键点的空间配置来提高对模糊候选预测的稳健性。在我们广泛的实验评估中,我们表明所提出的SCN在各种大小有限的2D和3D关键点检测数据集上的关键点定位误差方面优于相关方法,即手部X光片、头颅侧位片、手部MRI和脊柱CT。
Keywords: Anatomical landmarks; Localization; Fully convolutional networks; Heatmap regression
关键词:解剖学关键点;关键点定位;全卷积网络;热图回归
作者:Christian Payer 1 ) ^{1)} 1), Darko Štern 2 ) ^{2)} 2), Horst Bischof 1 ) ^{1)} 1), Martin Urschler 2 ) , 3 ) ^{2),3)} 2),3)
- Institute of Computer Graphics and Vision, Graz University of Technology, Graz, Austria (计算机图形与视觉研究所,格拉茨科技大学,格拉茨,奥地利)
- Ludwig Boltzmann Institute for Clinical Forensic Imaging, Graz, Austria (路德维希玻尔兹曼临床法医影像研究所,格拉茨,奥地利)
- Medical University of Graz, BioTechMed-Graz, Austria (格拉茨医科大学,格拉茨生物医学技术研究所,格拉茨,奥地利)
译者:丁纪翔 4 ) ^{4)} 4)
- 计算机科学与技术学院,华侨大学,福建厦门
原文链接:Payer C, Štern D, Bischof H, et al. Integrating spatial configuration into heatmap regression based CNNs for landmark localization[J]. Medical image analysis, 2019, 54: 207-219.
译文LaTex源码(计算机学报格式):https://cn.overleaf.com/read/vvhbdgfqbbfr
❤️ 如果你喜欢我的文章,可以通过点赞和收藏支持我。更多内容欢迎关注我的博客:https://blog.csdn.net/IYXUAN
文章目录
- 解剖学关键点检测方向论文翻译和精读:Integrating spatial configuration into heatmap regression based CNNs for landmark localization
-
- 1 引言
-
- 1.1 相关工作
- 1.2 贡献
- 2 方法
-
- 2.1 使用CNN对热力图进行回归分析
- 2.2 空间配置网络(SCN)
-
- 2.2.1 局部外观 ⇔ \Leftrightarrow ⇔空间配置
- 2.2.2 局部外观
- 2.2.3 空间配置
- 3 实验设置和训练细节
-
- 3.1 定位U-Net(Localization U-Net)
- 3.2 评价指标
- 4 评价和定量结果
-
- 4.1 手部X光片(2DHand)
-
- 4.1.1 完整手部X光片(2DHandFull)
- 4.1.2 部分手部X光片(2DHandReduced)
- 4.1.3 局部外观 ⇔ \Leftrightarrow ⇔空间配置
- 4.2 手部MRIs(3DHand)
- 4.3 头颅侧位X射线图像(2DSkull)
- 4.4 脊柱CT (3DSpine)
- 5 讨论和结论
- 致谢
- 参考文献
1 引言
解剖关键点的定位是医学图像分析的一个重要步骤,例如,基于可变形统计模型进行分割[1,2],初始化基于特征的图像配准[3,4],或者对检测到的解剖结构(如椎骨)进行参数化建模[5]。不幸的是,由于局部类似结构常常会引入模糊性,导致解剖标志的定位存在困难。这种模糊性使得很难降低关键点定位误差,误差越小则意味着对关键点错误识别的鲁棒性越强以及在每个已识别的关键点处的精度越高。为了应对这些困难,基于机器学习的方法主要被用来自动定位图像中的解剖关键点。这些方法通常将局部关键点预测与明确的显式手工定义的图模型相结合,旨在用训练数据中可见的有效空间配置约束预测。因此,我们将关键点定位任务分成两个连续的步骤来简化关键点检测的问题。第一步专门用于产生局部准确但可能模糊的候选预测,而在第二步中,使用图模型[6,7]消除模糊性,以提高对关键点错误识别的鲁棒性。
近年来,计算机视觉的进展主要是由深度卷积神经网络(CNN)推动的,因为它们具有从图像中自动学习重要特征的卓越能力[8,9]。它们不仅在许多计算机视觉任务[10,11],而且在许多医学图像分析应用中改进了现有技术[12,13]。与之前使用先验知识构建手工模型的关键点检测模型相反,深度卷积神经网络架构依靠大量的训练数据来自动学习可用有效空间配置约束预测的模型。在医学图像领域,大量训练数据的获取存在两方面挑战。首先,道德和财政问题阻碍了大规模的医疗图像的获取。其次,在有监督的情况下,需要训练有素的专家来创建关键点真实标注,这往往是困难、昂贵且耗时的。因此,与计算机视觉任务相比,基于CNN的医学图像分析方法必须能够处理数量明显偏少的有标注的训练数据。
我们假设,通过沿用手工图模型探索的思路,可以降低CNN对大量训练数据的需求。这样的模型包含了先验知识,即一个关键点的可行位置在图像空间中不是均匀分布的,而是受到其他解剖关键点位置的制约。因此,我们的假设是,这种关于关键点空间配置的先验知识可以使网络简化对可行的解剖空间配置潜在分布的建模,因此需要较少的训练数据。尽管空间配置的约束条件以前已经被用于计算机视觉,例如,用于语义分割[14]或识别姿势[15],但它们仅用于改善基于CNN的预测的鲁棒性,而不是基于先验知识来简化预测任务。在医学图像分析任务中,高局部准确性被认为与对关键点错误识别的鲁棒性同样重要,将解剖关键点的空间配置纳入CNN以便从有限的训练数据中进行学习还尚未被研究。
在本文中,我们展示了我们提出的双组件CNN能够通过学习利用空间配置信息来实现低关键点定位误差,即使只有有限的训练数据。我们的空间配置网络(SpatialConfiguration-Net,SCN)学习将其中一个组件用于提供局部准确但可能模糊的候选预测,而另一个组件则专注于融合空间配置,通过消除模糊性来提高对关键点错误识别的鲁棒性。因此,定位任务被分割成两个更简单的子问题,减少了对大型数据集的总体需求。在我们的定量评估中,我们表明我们提出的方法是广泛适用的,并在来自各种模态的四种大小有限的2D和3D医学图像分析数据集上优于现有最先进的方法,即手部X光片、头颅侧位片、手部MRI和脊柱CT。
1.1 相关工作
解剖学关键点检测的一个突出策略是将局部特征响应与编码关键点全局空间配置的手工图模型相结合。这种方法在医学图像分析中被广泛使用,因为只要训练数据具有代表性,它们就能有效地捕捉到解剖学变化,而不依赖于训练数据集的大小。例如,Liu等人[16]根据对其他关键点预测的相对位置,逐步限制了关键点的搜索空间。他们表明,这种限制大大降低了运行时间,同时也提供了优越的性能。一个广泛使用的纳入全局形状信息的方法是使用点分布模型[6]。
Lindner等人[17]通过使用一个约束的局部模型,在随机森林[18]生成的局部特征响应的基础上迭代完善全局关键点配置,在二维手部和颅骨X光片上表现出最先进的性能,从而扩展了这一策略。医学图像分析中经常使用的其他图形模型是马尔科夫随机场(MRFs)。它们已被成功用于许多应用中的关键点检测,如肺部分割[19]、脑部配准[20]、脊柱检测[21],以及全身CT扫描[22]、手部X光片[23]或牙齿MRI[24]分析。虽然这些最近的工作中有许多只使用随机森林框架来生成局部外观特征响应[17,21,23],但Ebner等人[25]调整了Criminisi等人[26]关于器官边界框定位的开创性工作,他们首先基于全局外观特征鲁棒地限制预测区域,然后基于局部特征进行精确定位。然而,他们的表现高度依赖于第一个级联阶段是否能提供鲁棒的预测,因为在第二阶段只能提高准确率。 后来,为了消除局部外观特征反应的假阳性预测,Urschler等人[27]将关键点的空间配置整合到一个使用全局外观以及几何特征的随机森林。因此,他们在一个统一的随机回归森林框架内模拟了MRF。
在ImageNet[28]等大型标注训练数据集的帮助下,计算机视觉方法最近出现了向深度学习和CNN的颠覆性转变。尽管医学成像领域的标注训练图像通常数量有限,但最近一些使用CNN的方法在解剖学关键点检测方面也取得了成功。对于椎骨的定位和识别,Chen等人[29]提出了一个三阶段的框架,结合了用于粗略标记关键点的随机森林、用于细化其位置信息的形状模型,以及用于识别关键点的CNN。他们的方法的缺点是,只使用2D CNN,因此无法充分利用3D CNN的立体信息。Zhang等人[30]通过首先将所有体素配准到一个模板体素,然后用单个CNN回归所有关键点坐标,同时从有限的脑部MR体素中同时检测数千个解剖关键点。然而,正如人类姿势估计方法所观察到的那样[31],直接回归坐标涉及从输入图像到点坐标的高度非线性映射[32]。
Tompson等人[15]提出了一种更简单的基于图像的映射方法,即基于回归热图像来进行映射,这些图像编码了一个地标在某个像素位置处被定位的伪概率。因此,他们用于人体姿态估计的网络学会了在接近目标关键点的位置上产生高响应,同时抑制错误位置上的响应。他们的工作还将MRF模型的二进制项整合到CNN架构中。然而,由于他们的方法是在图像块上训练来预测热力图图像的,而且他们的各个阶段是单独训练的,最后再进行微调,因此Tompson等人[15]的方法在关键点定位误差方面存在缺陷。在我们的初步工作中[33],我们也使用了热力图回归框架,然而,我们将关键点的空间信息直接整合到一个端到端的训练的全卷积网络中。我们的实验表明即使在训练数据量非常有限的情况下也有可能实现良好的性能。建立在我们在[33]中提出的方法的基础上,Yang等人[34]使用热力图回归框架,通过将邻近关键点的预训练模型纳入他们的CNN,来预测失响应的关键点。然而,与我们的方法直接减少类似关键点上的错误响应不同,他们通过一个额外的后处理步骤来消除假阳性反应。针对椎骨的识别和定位,Liao等人[35]提出了一个三阶段方法。他们预训练一个同时对椎骨进行分类和定位的网络,使用学到的权重来生成全卷积网络的响应,最后用双向循环神经网络去除假阳性响应。最近,Ghesu等人[36,37]研究了一种不同的策略。他们提出使用强化学习来生成指向所寻找的关键点的导航轨迹。他们的方法的局限性是需要大量的计算训练和非常大的数据集。
上述CNN方法要么需要大量的训练数据,要么需要复杂的后处理,要么不能同时适用于2D和3D数据。在本文中,我们提出了一个单一的端到端训练的全卷积网络,在有限的训练数据下在2D和3D应用中都能很好地工作,并且不需要任何特定于数据集的后处理。
1.2 贡献
我们建议将解剖关键点的空间配置纳入基于CNN的热力图回归框架,即使在有限的训练数据集的情况下也能提供低关键点检测误差。在我们的单阶段方法中,网络本身学习将一个组件用于产生局部准确但可能模糊的候选预测,而另一个组件只负责消除模糊性以提高对关键点错误识别的鲁棒性。通过单个的优化过程和端到端的方式进行训练,我们的全卷积空间配置网络(SpatialConfiguration-Net,SCN)的局部外观和空间配置组件专注于解决两个更简单的子问题,这些问题单独需要较少的训练数据。因此,从大型数据集中学习的总体需求被降低了。
这项工作中提出的方法扩展了我们早前的MICCAI论文[33],具体如下:
-
我们修改了目标函数,允许根据网络的预测置信度,分别学习每个关键点的最佳热力图生成函数(见第2.1节);
-
我们改变了局部外观组件的CNN结构,以更好地考虑到不同尺度的图像外观特征,以回归热力图并产生局部准确的候选预测(见第2.2.2节);
-
我们改进了空间配置组件,以允许关键点配置之间有更多的变化,展示了在消除局部相似结构方面的好处,特别适用于诸如椎骨识别和定位等具有挑战性的任务(见第2.2.3节);
-
我们展示了SCN在多种不同的医学成像数据集上的广泛适用性,包括2D的手部X光片和头颅侧位片,以及3D手部MRI和脊柱CT;
-
我们在所有研究的数据集上报告了关键点检测误差方面的新的最先进的结果,包括ISBI 2015头颅X射线图像分析挑战赛(Wang等人,2016)和MICCAI CSI 2014椎骨定位和识别挑战赛,该挑战赛涉及来自Glocker等人(2013)的病理脊柱CT。
2 方法
为了在有限的训练数据集中实现低关键点检测误差,我们提出的SCN架构直接结合了两个相互作用的组件的相应输出。如图1所示,当我们基于热力图回归的全卷积网络架构(第2.1节)以端到端方式进行训练时,这些组件的交互是通过两个组件产生的预测相乘来实现的。由于这种交互作用,我们的卷积网络学会了将其局部外观组件用于提供局部准确但可能模糊的候选预测,而其空间配置组件则通过消除模糊性,专注于提高对关键点错误识别的鲁棒性(见第2.2节)。当通过乘法结合时,这种相互作用的结果是低关键点检测误差,即在每个识别的关键点上具有强鲁棒性和高局部精度。

图1 在端到端训练的全卷积CNN框架中对每个关键点热力图进行回归来进行解剖关键点检测。在我们提出的SpatialConfiguration-Net (SCN)中,这两个组件通过逐元素乘法相互作用,使局部外观组件专注于产生局部准确但模糊的候选预测,而空间配置组件专注于减少模糊性以提高对关键点错误识别的鲁棒性。
2.1 使用CNN对热力图进行回归分析
虽然直接回归关键点坐标的CNN[30,31]需要具有许多网络参数的密集层来模拟高度非线性和难以学习的图像到坐标的映射,但我们的方法是基于回归热力图图像[15],它编码了关键点位于某个像素位置的伪概率。通过实现图像到图像的映射,我们因此从使用完全卷积网络[40]中受益,因为网络权重数量和计算复杂性都减少了。
具体而言,我们将包含 N N N个关键点的 d d d维图像的一个以 x i ∗ ∈ R d \stackrel{*}{\mathbf{x}_{i}} \in \mathbb{R}^{d} xi∗∈Rd为坐标的目标关键点 L i , i = { 1 , … , N } L_{i}, \quad i=\{1, \ldots, N\} Li,i={1,…,N}的热力图 g i ( x ) : R d → R g_{i}(\mathbf{x}): \mathbb{R}^{d} \rightarrow \mathbb{R} gi(x):Rd→R定义为高斯函数
g i ( x ; σ i ) = γ ( 2 π ) d / 2 σ i d exp ( − ∥ x − x ∗ i ∥ 2 2 2 σ i 2 ) \begin{equation} g_{i}\left(\mathbf{x} ; \sigma_{i}\right)=\frac{\gamma}{(2 \pi)^{d / 2} \sigma_{i}^{d}} \exp \left(-\frac{\left\|\mathbf{x}-\stackrel{*}{\mathbf{x}}_{i}\right\|_{2}^{2}}{2 \sigma_{i}^{2}}\right) \end{equation} gi(x;σi)=(2π)d/2σidγexp −2σi2 x−x∗i 22
因此,目标坐标 x i ∗ ∈ R d \stackrel{*}{\mathbf{x}_{i}} \in \mathbb{R}^{d} xi∗∈Rd附近的热力图像素具有较高的数值,而在远离 x i ∗ \stackrel{*}{\mathbf{x}_{i}} xi∗的地方,这些数值会平滑但迅速降低。我们引入了一个缩放系数 γ \gamma γ,以避免由于高斯函数产生非常小的值而导致的训练过程中数值的不稳定性。对每个维度 d d d来说,标准偏差 σ i \sigma _i σi定义了关键点l的热力图图像中高斯函数的峰值宽度。
不同于我们之前的工作[33]以及其他基于热力图的方法[15],我们将 σ i \sigma _i σi作为 g i g_i gi的一个未知参数,允许它在训练CNN时与网络权重 w \mathbf{w} w和偏差 b \mathbf{b} b一起学习。因此,我们可以根据网络的预测置信度,为每个关键点分别学习最佳热力图峰宽。
该网络通过最小化所有关键点 L i L_i Li的预测热力图 h i ( x ; w , b ) h_{i}(\mathbf{x} ; \mathbf{w}, \mathbf{b}) hi(x;w,b)和相应的目标热力图 g i ( x ; σ i ) g_i(\mathbf{x} ; \sigma _i) gi(x;σi)之间的差异,来学习同时回归 N N N个热力图:
min w , b , σ ∑ i = 1 N ∑ x ∥ h i ( x ; w , b ) − g i ( x ; σ i ) ∥ 2 2 + α ∥ σ ∥ 2 2 + λ ∥ w ∥ 2 2 \begin{equation} \begin{aligned} \min _{\mathbf{w}, \mathbf{b}, \boldsymbol{\sigma}} \sum_{i=1}^{N} \sum_{\mathbf{x}} \quad & \left\|h_{i}(\mathbf{x} ; \mathbf{w}, \mathbf{b})-g_{i}\left(\mathbf{x} ; \sigma_{i}\right)\right\|_{2}^{2} \\ & +\alpha\|\boldsymbol{\sigma}\|_{2}^{2}+\lambda\|\mathbf{w}\|_{2}^{2} \end{aligned} \end{equation} w,b,σmini=1∑Nx∑∥hi(x;w,b)−gi(x;σi)∥22+α∥σ∥22+λ∥w∥22
这个新的目标函数通过一个涉及热力图峰宽 σ = ( σ 1 , … , σ N ) T \boldsymbol{\sigma}=\left(\sigma_{1}, \ldots, \sigma_{N}\right)^{T} σ=(σ1,…,σN)T的 L 2 L_2 L2正则化项扩展了[33]。由于 σ \boldsymbol{\sigma} σ是可学习的网络参数,因此该项避免了 σ i → ∞ \sigma_{i} \rightarrow \infty σi→∞导致 g i ( x ; σ i ) ≈ 0 g_{i}\left(\mathbf{x} ; \sigma_{i}\right) \approx 0 gi(x;σi)≈0的平凡解。因子 α \alpha α定义了热力图峰宽 σ \boldsymbol{\sigma} σ的惩罚程度, λ \lambda λ控制了网络权重 w \mathbf{w} w的 L 2 L_2 L2范数的影响。
在(2)中, h i ( x ; w , b ) h_{i}(\mathbf{x} ; \mathbf{w}, \mathbf{b}) hi(x;w,b)和 g i ( x ; σ i ) g_i(\mathbf{x} ; \sigma _i) gi(x;σi)的 L 2 L_2 L2距离和惩罚项 σ \boldsymbol{\sigma} σ相互作用。为了使(2)最小化,前者倾向于较大的 σ \boldsymbol{\sigma} σ,而后者则迫使 σ \boldsymbol{\sigma} σ尽可能小。当网络对预测正确的关键点非常有信心时,它会预测更窄的热图峰宽,对于更不确定的关键点,它会预测更宽的峰宽,例如来自难以准确预测的关键点,则预测峰宽较宽。 因此,如图2所示,网络在大 σ i \sigma _i σi和小 σ i \sigma _i σi之间得到了最佳权衡,前者产生潜在不确定的预测,而后者则产生高精度响应的预测。
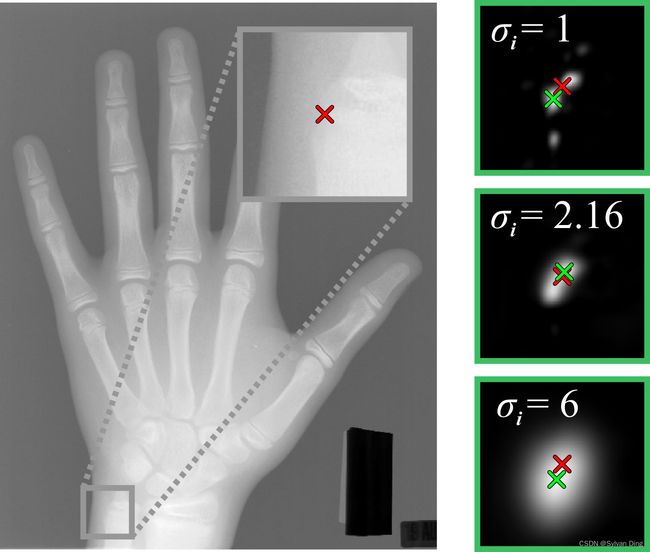
图2 不同的 σ i \sigma _i σi对关键点 L i L_i Li放大区域的热力图输出示例。上图显示了选择固定 σ i \sigma _i σi过小时的多个峰值;中图显示了学习 σ i = 2.16 \sigma _i=2.16 σi=2.16的响应;下图显示了固定 σ i \sigma _i σi过大时的过度平滑响应。目标坐标 x ∗ i \stackrel{*}{\mathbf{x}} _{i} x∗i由 × \times ×描述,预测坐标 x ^ i \hat{\mathbf{x}} _{i} x^i由 × \times ×描述。
在网络推断中,我们通过取热力图的最高值的坐标来获得每个关键点 L i L_i Li的预测坐标 x ^ i ∈ R d \hat{\mathbf{x}}_{i} \in \mathbb{R}^{d} x^i∈Rd:
x ^ i = arg max x h i ( x ; w , b ) . \begin{equation} \hat{\mathbf{x}}_{i}=\arg \max _{\mathbf{x}} h_{i}(\mathbf{x} ; \mathbf{w}, \mathbf{b}) . \end{equation} x^i=argxmaxhi(x;w,b).
2.2 空间配置网络(SCN)
热力图回归的SCN的基本概念是其两个组成部分之间的相互作用,分别代表局部外观和空间配置(见图3)。在第2.2.1节中,我们解释了这两个组件是如何互动的,以便将定位任务简化为两个子问题。虽然两个相互作用的组件在其结构方面原则上是灵活的,但在第2.2.2和2.2.3节中,我们描述了我们为这两个组件提出的结构。

图3 我们提出的SCN架构示意图。在局部外观组件部分,输入图像 I I I被转换成 H L A \mathbb{H}^{\mathrm{LA}} HLA,代表 N N N个关键点的局部外观热力图。黑色虚线表示 H L A \mathbb{H}^{\mathrm{LA}} HLA被用作空间配置组件的输入,其中 H L A \mathbb{H}^{\mathrm{LA}} HLA被转化为空间配置热力图 H S C \mathbb{H}^{\mathrm{SC}} HSC. H L A \mathbb{H}^{\mathrm{LA}} HLA和 H S C \mathbb{H}^{\mathrm{SC}} HSC逐元素相乘的到最终的热力图预测结果 H \mathbb{H} H. 空框代表中间图像;箭头代表连接,即 → \to →卷积、 → \to →下采样、 → \to →上采样; ⊕ \oplus ⊕代表像素级加法, ⊙ \odot ⊙代表像素级乘法。
2.2.1 局部外观 ⇔ \Leftrightarrow ⇔空间配置
对于 N N N个关键点,通过两个组件对应的热图输出的逐元素乘积 ⊙ \odot ⊙,得到预测热图集 H = { h i ( x ) ∣ i = 1 … N } \mathbb{H}=\left\{h_{i}(\mathbf{x}) \mid i=1 \ldots N\right\} H={hi(x)∣i=1…N}:
h i ( x ) = h i L A ( x ) ⊙ h i S C ( x ) \begin{equation} h_{i}(\mathbf{x})=h_{i}^{\mathrm{LA}}(\mathbf{x}) \odot h_{i}^{\mathrm{SC}}(\mathbf{x}) \end{equation} hi(x)=hiLA(x)⊙hiSC(x)
其中,由于符号简便起见,省略了网络权重 w \mathbf{w} w和偏置 b \mathbf{b} b。 h i L A ( x ) h_{i}^{\mathrm{LA}}(\mathbf{x}) hiLA(x)和 h i S C ( x ) h_{i}^{\mathrm{SC}}(\mathbf{x}) hiSC(x)分别是每个关键点 L i L_i Li的局部外观和空间配置组件的输出。
这两个部分通过(4)中的乘法相互作用。这个乘法对SCN学习简化定位任务至关重要,因为它强制要求两个组件在目标关键点 x i \mathbf{x}_{i} xi的位置上产生响应,即 h i L A ( x ) h_{i}^{\mathrm{LA}}(\mathbf{x}) hiLA(x)和 h i S C ( x ) h_{i}^{\mathrm{SC}}(\mathbf{x}) hiSC(x)都对靠近 x i ∗ \stackrel{*}{\mathbf{x}_{i}} xi∗的位置都会产生响应,而在所有其他位置上,只要其中一个组件没有响应,另一个组件就可以有响应。因此,只要空间配置组件在局部类似结构的位置上没有响应,局部外观组件就可以专注于将输入图像转化为目标关键点 x i ∗ \stackrel{*}{\mathbf{x}_{i}} xi∗位置上的局部高度准确的响应,而不需要抑制局部相似结构。另一方面,只要局部外观组件在 x i ∗ \stackrel{*}{\mathbf{x}_{i}} xi∗的位置上产生一个局部高度准确的响应,空间配置组件就可以通过消除局部外观组件输出的假阳性响应来专注于区分局部相似结构,而无需在 x i ∗ \stackrel{*}{\mathbf{x}_{i}} xi∗的位置上产生高度准确的响应。
相比之下,以前的工作[15,32]旨在同时实现对于关键点识别的鲁棒性和每个网络组件中识别的局部准确性,其缺点是无法实现定位任务的简化。另一方面,我们的架构导致了一个解决方案,即两个组件都面临更简单的任务,可以从更少的训练数据中学习。
2.2.2 局部外观
由于(4)中的乘法,局部外观组件的主要重点是将输入图像 I I I转化为一组局部准确但可能模糊的热力图 H L A = { h i L A ( x ) ∣ i = 1 … N } \mathbb{H}^{\mathrm{LA}}=\left\{h_{i}^{\mathrm{LA}}(\mathbf{x}) \mid i=1 \ldots N\right\} HLA={hiLA(x)∣i=1…N}。因此,对于每个关键点 L i L_i Li,局部外观组件生成热力图输出 h i L A ( x ) h_{i}^{\mathrm{LA}}(\mathbf{x}) hiLA(x),仅在关键点坐标 x i ∗ \stackrel{*}{\mathbf{x}_{i}} xi∗的附近与高斯目标 g i ( x ) g_i(\mathbf{x}) gi(x)相似。这是通过一个受全卷积网络[40,41]和残差网络[42]启发的多级结构实现的。如图3的局部外观部分所示,每个层次由几个连续的卷积层组成。在多级结构中,每个级别的最后一个卷积层之前连接的平均池化层在我们的收缩路径中以一半的分辨率生成下一个低级别的输入。在扩展路径中,每一层的输出都被线性上采样以使分辨率加倍。这些上采样的输出被添加到下一个更高层次的最终卷积层的输出中。每一层的输出代表了对下一层的残差,因此中间的热力图被迭代细化,同时分辨率增加,直到再次达到原始分辨率。在具有原始分辨率的最高层的最后一个卷积层产生了一组局部外观热力图 H L A \mathbb{H}^{\mathrm{LA}} HLA。
与Ronneberger等人[41]等其他全卷积网络架构相比,我们的局部外观组件的扩展路径使用较少的参数,使得SCN的训练速度更快。
2.2.3 空间配置
由于(4)中的乘法,空间配置组件的主要重点是将局部准确但模糊的热力图 H L A \mathbb{H}^{\mathrm{LA}} HLA从局部外观组件中区分出来,从而为定位提供对关键点错误识别的鲁棒性。空间配置组件仅使用局部外观热图 H L A \mathbb{H}^{\mathrm{LA}} HLA作为其输入,通过学习如何从所有关键点的局部位置预测 H L A \mathbb{H}^{\mathrm{LA}} HLA中鲁棒地预测单个关键点的位置,隐式地将关键点的空间配置几何模型纳入其中。通过将整个局部外观热力图 H L A \mathbb{H}^{\mathrm{LA}} HLA转化为每个关键点 L i L_i Li的单个热力图 h i S C ( x ) h_{i}^{\mathrm{SC}(\mathbf{x})} hiSC(x), h i S C ( x ) h_{i}^{\mathrm{SC}(\mathbf{x})} hiSC(x)在靠近目标 x i ∗ \stackrel{*}{\mathbf{x}_{i}} xi∗的坐标 x \mathbf{x} x上提供响应,并抑制其他地方的响应。因此,在我们的空间配置组件中,通过将响应限制为可行的关键点配置, h i S C ( x ) h_{i}^{\mathrm{SC}(\mathbf{x})} hiSC(x)中的错误响应被抑制。
如图3的空间配置部分所示,我们用连续的卷积层来建模从 H L A \mathbb{H}^{\mathrm{LA}} HLA到 H S C = { h i S C ( x ) ∣ i = 1 … N } \mathbb{H}^{S C}=\left\{h_{i}^{S C}(\mathbf{x}) \mid i=1 \ldots N\right\} HSC={hiSC(x)∣i=1…N}的转换。为了覆盖关键点之间的空间,这些卷积层需要有大的感受野。由于在空间配置部分不需要很高的局部精度,因此卷积层可以在比局部外观部分更低的分辨率上计算,这也使得卷积核的大小和计算复杂度保持相对较小。在对 H L A \mathbb{H}^{\mathrm{LA}} HLA进行下采样后,连续的卷积层生成下采样版本的热力图 H S C \mathbb{H}^{S C} HSC,并通过上采样层将其大小调整为和 H L A \mathbb{H}^{\mathrm{LA}} HLA相同。因此, H L A \mathbb{H}^{\mathrm{LA}} HLA和 H S C \mathbb{H}^{S C} HSC具有相同的大小,以实现(4)中给出的逐元素相乘操作。
与我们以前的工作[15,33]不同,它们只允许建模成对关系,如MRF模型,而多个卷积层能够建立关键点之间更复杂的关系。 这大大增加了网络所能代表的关键点配置的可变性。此外,多个层以较小的卷积核捕获相同大小的感受野,从而减少了捕获关键点空间配置所需的参数数量。因此,我们的连续卷积层增加了网络的潜在表示能力,同时保持了网络参数并维持了计算复杂度的低水平。
3 实验设置和训练细节
网络的训练和测试是在Tensorflow中完成的。对网络输入图像的预处理如下。对于数据集中的每张图像,我们保持网络输入图像和输出热力图的像素大小不变。输入图像以固定的长宽比重新调整,以适应网络输入的图像尺寸,而网络输出在使用(3)生成最终的关键点坐标预测值 X ^ i \hat{\mathbf{X}}_{i} X^i之前被重新调整为原始输入图像的尺寸。此外,每个数据集的强度范围被缩放到 [ − 1 , 1 ] [-1, 1] [−1,1]范围之内,方法是用来自数据集的最小和最大强度派生的相同值来移动和缩放图像的每个像素/体素。与我们之前的工作[33]相比,我们既没有减去输入图像的平均值,也没有归一化标准差。
我们使用SimpleITK进行即时的数据增强。强度值被随机地乘以 [ 0.75 , 1.25 ] [0.75, 1.25] [0.75,1.25],并移动 [ − 0.25 , 0.25 ] [-0.25, 0.25] [−0.25,0.25]。图像被随机平移 [ − 20 , 20 ] [-20, 20] [−20,20]像素,旋转 [ − 1 5 ∘ , 1 5 ∘ ] [-15^{\circ} , 15^{\circ} ] [−15∘,15∘],缩放 [ − 0.6 , 1.4 ] [-0.6, 1.4] [−0.6,1.4]。我们还通过在规范的 12 × 12 12\times12 12×12像素网格上随机移动点,并使用三次B样条进行插值,实现弹性变形。所有的增强操作都是从指定区间内的均匀分布中随机取样。我们的即时训练工具和实现的CNN架构的代码是公开的1。
除非另有说明,否则我们将SCN的参数设置如下。局部外观组件有四个级别,每个级别包含三个具有 128 128 128个输出的连续 3 × 3 3\times3 3×3(3D: 3 × 3 × 3 3\times3\times3 3×3×3)卷积层,第二个卷积层后的 2 × 2 2\times2 2×2(3D: 2 × 2 × 2 2\times2\times2 2×2×2)平均池化生成下一级别。我们在每级的第一个卷积层后添加 D r o p o u t = 0.5 \mathrm{Dropout}=0.5 Dropout=0.5[43]以改善泛化性能。局部外观热图H1是由具有与关键点数量相等的输出数的 3 × 3 3\times3 3×3(3D: 3 × 3 × 3 3\times3\times3 3×3×3)卷积层生成的。空间配置部分是以输入分辨率的 1 16 \frac{1}{16} 161(3D: 1 4 \frac{1}{4} 41)计算的。它由具有 128 128 128个输出的三个连续的 11 × 11 11\times11 11×11(3D: 7 × 7 × 7 7\times7\times7 7×7×7)卷积层和一个具有与地标数量相等的输出数的附加的 11 × 11 11\times11 11×11(3D: 7 × 7 × 7 7\times7\times7 7×7×7)卷积层组成。这这些输出使用双/三次插值上采样回输入分辨率以生成 H S C \mathbb{H}^{S C} HSC。整个SCN的每个中间卷积层都具有负斜率为0.1的LeakyReLU[44]激活函数,以便在训练时容易收敛。生成 H L A \mathbb{H}^{\mathrm{LA}} HLA的卷积层具有线性激活函数;生成 H S C \mathbb{H}^{S C} HSC的卷积层具有Tanh激活函数,以限制输出在-1到1之间。卷积层的偏差初始化为0,权重使用[11]中描述的方法进行初始化,除了生成热图 H L A \mathbb{H}^{\mathrm{LA}} HLA和 H S C \mathbb{H}^{S C} HSC的层。在这里,初始权重从标准差为0.001的高斯分布中绘制。需要这些小的权重以生成初始热图响应接近于0,否则网络训练将无法收敛。
训练网络时,我们使用参数 γ \gamma γ=100(3D: γ \gamma γ=1000)和 λ \lambda λ=0.0005的目标函数(2),这些参数是在初步实验中经验确定的。为确定参数 α \alpha α=20,我们在手部X射线数据集上进行了实验,该实验在第4.1节中描述。对于3D数据集,我们依据经验设置 α \alpha α=1000。我们使用Nesterov加速梯度下降算法[45](Nesterov’s Accelerated Gradient)最小化目标函数,学习率为 1 0 − 6 10^{-6} 10−6,动量为0.99。我们设置mini-batch=1,因为使用更大的mini-batch我们没有看到结果的改进,只是增加了训练时间和内存消耗。这些参数对于我们测试的所有数据集都保持不变。
我们通过在80%的训练图像上训练网络来确定每个被评估的数据集的训练迭代次数,并将剩余20%的训练图像作为验证集,以评估验证误差何时达到稳定状态。 对于用交叉验证法评估的数据集,我们通过评估第一折的验证损失来确定初始实验的训练迭代次数。然后对数据集的所有折进行训练,以确定迭代次数。
3.1 定位U-Net(Localization U-Net)
为了比较我们提出的SCN与全卷积架构,我们采用了基于U-Net[41]的架构,其在各种医学图像分割应用中表现出最先进的性能,例如在Sirinukunwattana等人[13]的工作中。根据热图回归的关键点定位任务,我们采用了其多尺度架构,建立了具有 5 5 5个级别和 128 128 128个输出的定位U-Net(Localization U-Net),从而类似于比我们SCN的局部外观组件更深的架构。在最深的两个级别中,我们实施了Dropout[41]。我们在卷积使用 P a d d i n g \mathrm{Padding} Padding以保持输入和输出图像大小相同。此外,我们使用平均池化而不是最大池化,并使用固定的线性上采样而不是反卷积。在我们的定位U-Net实现中进行了一些参数调整实验后,我们发现这些修改比原始的[41]实现具有更快的训练速度和更高的检测精度。此外,进一步增加级别和卷积输出的数量,即定位U-Net的深度,没有显示出任何改进。我们使用与SCN相同的损失函数训练定位U-Net,该函数也学习了最佳的热图参数 δ \delta δ.
3.2 评价指标
关键点检测方法的性能可以从局部准确性和对关键点错误识别的鲁棒性两方面来描述。对于图像 j j j中的每个标记点 L i L_i Li,点对点误差被定义为目标坐标 x i ∗ ( j ) ∈ R d \mathbf{x}_{i}^{*(j)} \in \mathbb{R}^{d} xi∗(j)∈Rd和预测坐标 x i ∗ ( j ) ∈ R d \mathbf{x}_{i}^{*(j)} \in \mathbb{R}^{d} xi∗(j)∈Rd之间的欧氏距离。为了弥补数据集中未知或变化的尺度,点对点误差乘以一个基于特定选定标记点的欧几里得距离的图像特定归一化因子 s ( j ) s^{(j)} s(j)。对于图像 j j j中的标记点 L i L_i Li,归一化点对点误差定义为:
P E i ( j ) = s ( j ) ∥ x i ∗ ( j ) − x ^ i ( j ) ∥ 2 \begin{equation} \mathrm{PE}_{i}^{(j)}=\boldsymbol{s}^{(j)}\left\|\mathbf{x}_{i}^{*(j)}-\hat{\mathbf{x}}_{i}^{(j)}\right\|_{2} \end{equation} PEi(j)=s(j) xi∗(j)−x^i(j) 2
这样可以计算出所有图像在所有关键点上的点对点误差的中位数、平均值和标准差(SD),即 P E a l l \mathrm{PE_{all}} PEall。我们还报告了所有图像中超出一定点对点误差半径 r r r的预测关键点 L i L_i Li的数量,即离群点的数量:
# O r = ∣ { ( j , i ) ∣ P E i ( j ) > r } ∣ \begin{equation} \# \mathrm{O}_{r}=\left|\left\{(j, i) \mid \mathrm{PE}_{i}^{(j)}>r\right\}\right| \end{equation} #Or= {(j,i)∣PEi(j)>r}
对单一图像 j j j的所有关键点进行计算,我们定义图像特定的点对点误差 I P E ( j ) \mathrm{IPE}^{(j)} IPE(j)为
IPE ( j ) = 1 N ∑ i = 1 N P E i ( j ) \begin{equation} \operatorname{IPE}^{(j)}=\frac{1}{N} \sum_{i=1}^{N} \mathrm{PE}_{i}^{(j)} \end{equation} IPE(j)=N1i=1∑NPEi(j)
其中 N N N是关键点的数量。与表征所有图像中所有关键点的离群值总数的 # O r \#O_r #Or不同的是,IPE提供了,IPE提供了一定误差半径内离群点的图像数量的信息。我们展示了IPE的累积分布图,它给出了达到一定IPE的测试图像的比例。
为了与脊柱CT扫描数据集上的其他方法进行比较,我们计算了正确识别关键点的数量。根据Glocker等人[39]的定义,如果最近的地面实证关键点是正确的,并且从预测位置到真实位置的距离小于20毫米,则被认为是正确识别的关键点。
正确识别关键点的数量被定义为
# I D = ∣ { ( j , i ) ∣ arg min k ∥ x ∗ k ( j ) − x ^ i ( j ) ∥ 2 = i ∧ P E i ( j ) ≤ 20 } ∣ \begin{equation} \# \mathrm{ID}=\left|\left\{(j, i) \mid \quad \underset{k}{\arg \min }\left\|\stackrel{*}{\mathbf{x}}_{k}^{(j)}-\hat{\mathbf{x}}_{i}^{(j)}\right\|_{2} =i \wedge \mathrm{PE}_{i}^{(j)} \leq 20\right\} \right| \end{equation} #ID= {(j,i)∣kargmin x∗k(j)−x^i(j) 2=i∧PEi(j)≤20}
为了与其他方法进行比较, I D r a t e \mathrm{ID_{rate}} IDrate被定义为正确识别的关键点在所有关键点中的百分比。
4 评价和定量结果
我们将我们提出的SCN架构与医学成像领域中各种最先进的定位方法在四个数据集上进行了比较,即左手的X光片(2DHand)、左手的立体MR扫描(3DHand)、头颅侧位片(2DSkull)和脊柱的立体CT扫描(3DSpine)。图4显示了所有数据集的代表性例子。

图4 被评估数据集的样本图像。体积投射到二维冠状面和矢状面图像上,用于可视化。圆圈表示关键点标注。
我们用12GB内存的NVIDIA Geforce Titan Xp来训练和测试我们的网络。训练一个网络,2DSkull大约需要4小时,2DHand和3DHand需要6小时,3DSpine需要20小时。测试2D图像大约需要2秒,测试3D体积图像大约需要5秒。
4.1 手部X光片(2DHand)
我们使用一个公开的手部X光片数据集2,与最先进的解剖标志定位算法进行比较,并详细研究我们的SCN的一些超参数。该数据集由使用不同的X光扫描仪获取的895个左手的放射状图像组成,平均大小为 1563 × 2169 1563\times2169 1563×2169像素。我们对指尖和骨关节上的37个特征关键点进行了人工标注。由于图像缺乏有关物理像素分辨率的信息,我们计算了一个图像特定的归一化因子 s ( j ) s^{(j)} s(j)。使用与[17,24,33]相同的归一化方法,我们假设手腕宽度为50毫米,由手腕处的两个注释标志确定,即 s ( j ) = 50 / ∥ x ∗ l w r i s t ( j ) − x ∗ r _ w r i s t ( j ) ∥ 2 \boldsymbol{s}^{(j)}=50 /\left\|\stackrel{*}{\mathbf{x}}_{\mathrm {l_wrist }}^{(j)}-\stackrel{*}{\mathbf{x}}_{\mathrm{r}_{\_} \mathrm {wrist}}^{{(j)}}\right\|_{2} s(j)=50/ x∗lwrist(j)−x∗r_wrist(j) 2。我们使用与[24,33]描述的相同的三折交叉验证设置,他们将895个输入图像分成三个部分,每个部分具有大约600个训练和300个测试图像。此外,我们使用与[24,33]相同的输入图像预处理,通过在手的轮廓内计算Otsu阈值,仅在参考图像内执行直方图匹配。我们网络迭代训练次数为30,000次。
4.1.1 完整手部X光片(2DHandFull)
我们在2DHandFull数据集上比较了我们的SCN与我们之前的工作[33]和其他最先进的方法的结果,表1列出了关键点定位误差的点对点误差( P E a l l \mathrm{PE_{all}} PEall)。此外,我们还报告了不同误差半径下的异常值数量( # O r \#O_r #Or),以评估对关键点错误识别的鲁棒性。可以从图5中以累积分布的形式看到所识别的关键点局部精度的点对点误差(IPE)。
表1 来自2DHandFull数据集的895张图像的三折交叉验证结果,每幅图像包含37个标注的关键点

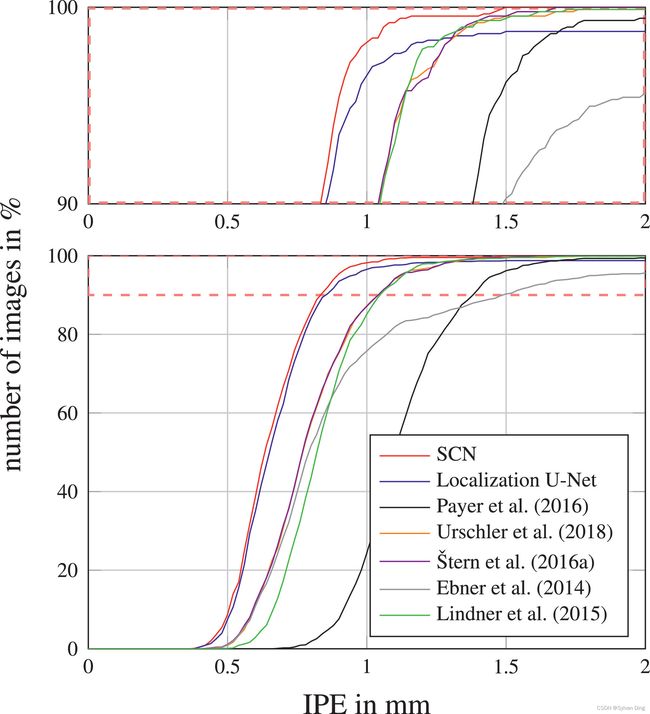
图5 2DHandFull数据集上图像特定的点对点误差的累积分布。红色虚线框内的放大区域显示在上面。(关于本图例中对颜色的解释,请读者参考本文的网络版)
从表1和图5中,我们看到,与我们以前[33]的工作相比,我们提出的SCN使用 512 × 512 512\times512 512×512像素的输入/热力图目标图像,在关键点检测误差方面有明显的改善。为了与先前工作使用 256 × 256 256\times256 256×256像素作为输入图像尺寸进行公平的比较,并研究输入尺寸超参数的影响,我们在二维手部数据集上做了一个实验,改变输入/热力图目标尺寸为128和512像素。这个实验的结果显示为图6中的累积IPE分布,表明即使输入/热力图目标尺寸减少到 128 × 128 128\times128 128×128像素,我们的表现也优于我们以前的工作。因此,与以前的工作相比,我们观察到的改进并不是来自输入/热力图目标尺寸的增加,而是来自以下两个扩展。
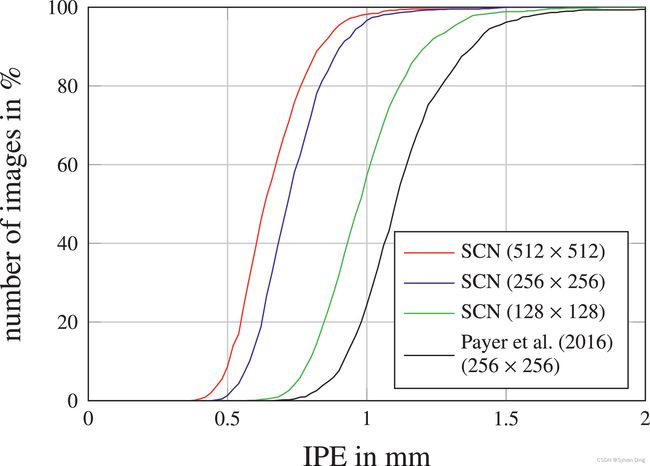
图6 我们的SCN架构在不同的输入/热力图目标尺寸下,2DHandFull数据集的IPE累积分布。
首先,我们修改后的局部外观组件增加了感受野的范围,这是因为残差结构增加了模型的深度级别[42]。我们分析了该组件受不同卷积输出数量的影响,当其在32和256之间变化时只产生了微小差异,而128和256之间的差异则无法区分。因此,我们在所有后续实验中都使用128个卷积输出,因为这个选择可以加快训练速度。
其次,定位性能的提高也来自于我们新的目标函数,其中涉及每个关键点的可学习热力图峰宽 σ \boldsymbol{\sigma} σ。为了研究这个扩展的行为,我们做了一个实验,将所有 σ i \sigma _i σi设置为不同的固定值[33],和设定不同加权因子 α \alpha α并将 σ \boldsymbol{\sigma} σ设置为每个关键点独立学习的变量进行对比。图7显示了这个实验的结果,它证实了独立变化 σ \boldsymbol{\sigma} σ胜过所有关键点 L i L_i Li固定 σ i \sigma _i σi,而 α \alpha α变化对定位性能的影响很小,表明这是一个不重要的参数。通过独立学习的 α \alpha α值,热图峰宽度会通过编码网络预测的不确定性来适应数据,见图2。易于精准预测的关键点会形成比那些在训练数据集中显示更多不确定性或模糊性的关键点更小的 σ i \sigma _i σi。因此,与固定的 σ i \sigma _i σi值相比,独立变化 σ \boldsymbol{\sigma} σ不需要在预先确定的过大 σ i \sigma _i σi产生过度平滑的、可能不准确的预测和过小 σ i \sigma _i σi导致可能高度准确但具有多个接近的峰值之间进行权衡。
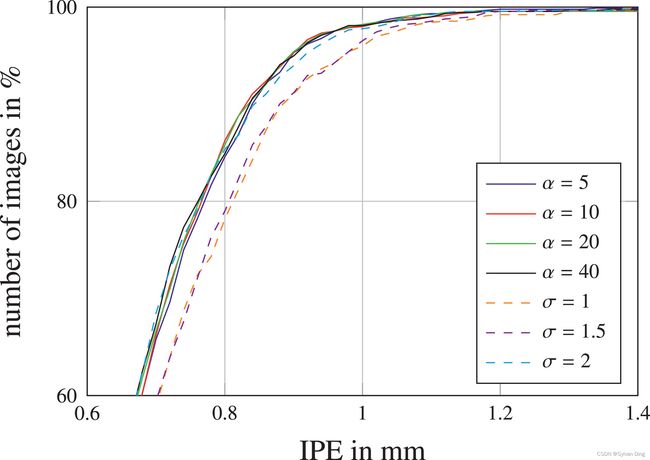
图7 在SCN学习 σ \boldsymbol{\sigma} σ时,固定 σ \sigma σ和不同加权因子 α \alpha α在2DHandFull数据集上的IPE的累积分布。
当将我们提出的SCN与其他最先进的算法进行比较时,图5和表1显示,它明显优于我们以前的所有方法,即只依靠随机回归森林的方法\cite{25,27},或另外结合显式图形模型的方法[24],以及我们以前基于CNN的方法[33]。此外,我们的SCN也优于Lindner等人[46]的最先进的关键点检测方法,他们将其算法应用于我们的预处理的2DHandFull数据集,并进行了相同的交叉验证划分。总的来说,对于这个数据集,我们的SCN实现了前所未有的三个10毫米异常值的离群点的低数量。有趣的是,在 # O r \#O_r #Or方面,我们优化的定位U-Net在2DHandFull数据集上的表现几乎与SCN一样好(见表1)。这可能是由于U-Net的深度架构接受了相对较多的训练数据所产生的结果。然而,从图5的累积IPE分布中,我们看到在1.25毫米的误差半径时,定位U-Net与其他大多数最先进的方法相比,性能有所下降。因此,从 # O r \#O_r #Or和IPE的结果可以得出结论,定位U-Net减少了图像中的离群点,而像Lindner等人[17]或Urschler等人[27]这样融合图形模型的方法减少了有离群点的图像,但也增加了每个图像上的离群点。
4.1.2 部分手部X光片(2DHandReduced)
在这个实验中,我们使用2DHandFull数据集的895张图像,系统地评估了我们的提出的SCN在减少训练图像数量的情况下的表现,同时仍使用与之前相同的三折交叉验证设置。因此,为了生成2DHandReduced,我们不是在每个折叠中使用所有的600张训练图像,而是只在10、50或100张图像的随机子集上进行训练,而在每个折叠中使用同样的300张图像进行测试,这样,每张图像仍然被测试一次。其他训练超参数与第4.1.1节中的相同。对于每一轮10张、50张和100张训练图像的交叉验证,我们以三次实验的平均值来报告我们的评估指标,以补偿随机选择的图像子集。
图8和表2中的实验结果显示,对于较小的训练数据集,我们的SCN比定位U-Net表现得好得多,因为当我们的SCN-10仅由10张图像训练时,在r=10mm处有30个离群值,而由10张图像训练的定位U-Net-10在相同的误差半径下有633个离群值。即使在100张图像上训练,本地化U-Net-100仍然有151个离群值。有趣的是,当用50张图片进行训练时,我们的SCN-50的关键点检测性能就已经与在2DHandFull数据集上训练的原始SCN几乎一样了。这个实验表明,增加训练图像的数量会使基于CNN的方法的定位性能普遍提高,同时也证实了我们的假设,即通过将空间配置纳入我们的SCN中,较少的数据量就足以进行训练。
表2 来自2DHandReduced数据集895张图像的交叉验证结果,以三个随机选择的训练图像的平均值为结果
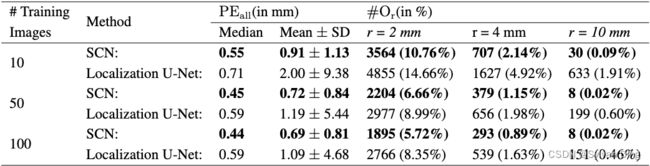
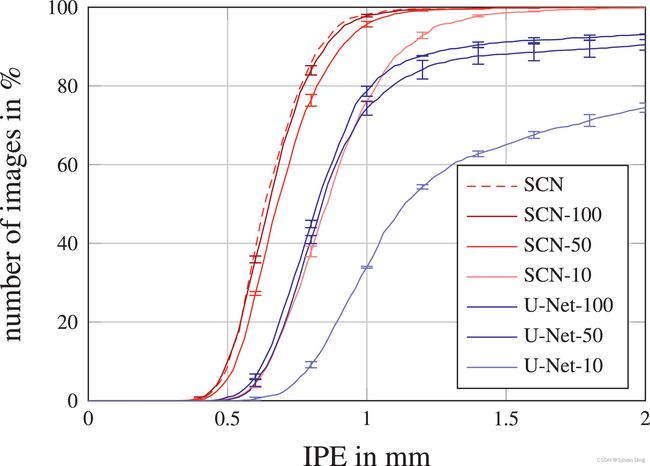
图8 不同数量的训练图像在2DHandReduced数据集上的IPE的累积分布。
4.1.3 局部外观 ⇔ \Leftrightarrow ⇔空间配置
正如在2DHandFull和2DHandReduced的实验中所显示的,在我们的工作中,没有必要提供大量的训练数据来实现低关键点检测误差。这是由于通过将本地外观和空间配置组件的预测结果相乘,将定位问题分解为两个更简单的任务,如图3所示。我们再次使用2DHandFull数据集在一个实验中展示了这种简化,我们分别提取正常训练的SCN的 H L A \mathbb{H}^{\mathrm{LA}} HLA和 H S C \mathbb{H}^{\mathrm{SC}} HSC两个部分的热力图的最大值。这个实验的结果在图9中给出,分别是LA和SC的IPE的累积分布。
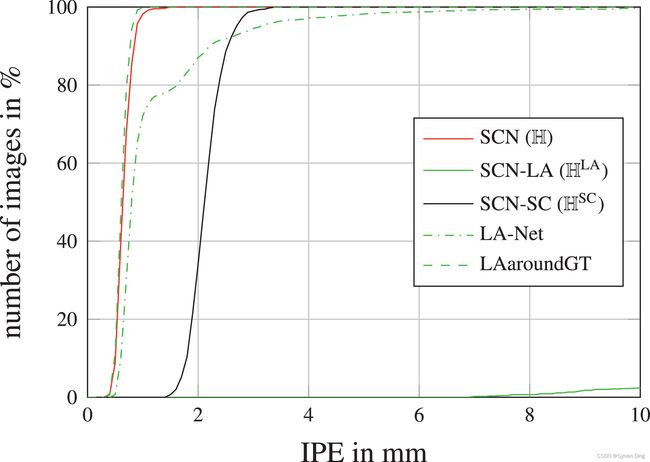
图9 在2DHandFull数据集上,我们的SCN的局部外观(LA)和空间配置(SC)组件的IPE累积分布(见图3)。LAaroundGT显示了在测试过程中限制在人工提供的地面真实关键点位置的10毫米半径内的LA预测。
为了证明SCN的性能提高不仅仅是由改进的LA组件引起的,我们做了一个实验,训练了一个仅由LA组件组成的网络(LA-Net)。由于LA-Net的感受野减少和缺少空间配置组件,它的表现不仅比SCN差(见图9),也比定位U-Net差(与图5相比)。
此外,我们通过在测试过程中提供真实的关键点位置,人为地产生了我们SCN的局部外观组件的结果。因此,在图9中,虚线LAaroundGT表示在10mm半径范围内由真实局部位置产生的预测。然而,由于模糊的组织结构,这些预测既不是唯一的预测,也不是在局部外观热力图 H L A \mathbb{H}^{\mathrm{LA}} HLA中产生响应最强的预测,如图3所示,也由图9中LA的累积误差分布的低值显示。尽管如此,当把局部准确但模糊的候选预测从局部外观热力图 H L A \mathbb{H}^{\mathrm{LA}} HLA与鲁棒但不准确的空间配置组件 H S C \mathbb{H}^{\mathrm{SC}} HSC结合起来时,局部外观组件结果的模糊性被消除了,而我们提出的SCN的局部准确性与LAaroundGT基本相同。
4.2 手部MRIs(3DHand)
为了显示我们的SCN对体积核磁共振(MR)图像的适用性并与我们以前发表的结果进行比较,我们使用了一个内部数据集,包括60个T1加权成像的3D核磁共振梯度回波手部扫描,其中有28个标注的关键点用于自动法医年龄估计[47]。平均体积大小为 294 × 512 × 72 294 \times 512 \times 72 294×512×72,体素分辨率为 0.45 × 0.45 × 0.9 0.45 \times 0.45 \times 0.9 0.45×0.45×0.9 mm。体积的输入和热力图目标尺寸为 96 × 128 × 32 96 \times 128 \times 32 96×128×32体素。SCN在局部外观模块中使用 3 × 3 × 3 3\times3\times3 3×3×3卷积核;对于空间配置模块,我们使用1/4的下采样系数,以及 7 × 7 × 7 7\times7\times7 7×7×7卷积核。对于U-Net的实现,我们使用 3 × 3 × 3 3\times3\times3 3×3×3的卷积核和四个深度级别。对于SCN和U-Net来说,每个中间卷积层卷积的输出数量被设置为64。我们使用与文献[25,27,33]相同的五重交叉验证设置,每轮包括43张训练图像和17张测试图像。我们对网络进行20,000次迭代训练。由于我们知道每张图像的物理体素分辨率, s ( j ) s^{(j)} s(j)被设置为1。
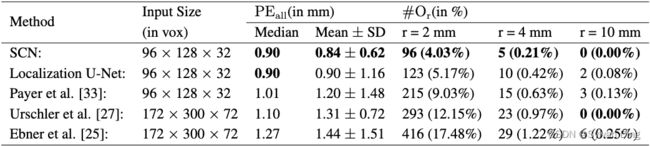
在表3中,我们将结果与我们以前的工作[25,27,33]进行了比较。我们的结果表明,在所有比较的方法中,我们的3D SCN对3D MR图像的定位性能最好。在两种方法使用相同体素分辨率的情况下,我们的关键点检测误差( P E a l l \mathrm{PE_{all}} PEall)明显优于Payer等人[33]的初步工作。与基于随机回归森林的方法[25,27]相比,我们在定位误差方面也明显更好,尽管这些方法在每个维度使用双倍的体素分辨率。有趣的是,除了我们提出的方法,唯一在此数据集上在r=10mm处实现优秀离群点率的其他方法也利用了关于关键点的空间配置的信息[27]。除了我们提出的3D SCN显示出最佳的定位性能外,在这个仅由60个体积组成的小数据集上,定位U-Net也超过了我们之前的所有方法。我们推测,这种良好的性能来自于我们的三维数据增强方案,涉及弹性和强度变换,这对训练这种深度CNN非常有利。
表3 来自3DHand的60张图像的交叉验证结果,每幅图像包含28个标注的关键点
4.3 头颅侧位X射线图像(2DSkull)
为了比较我们提出的SCN在关键点定位挑战中的效果,我们将其应用于ISBI 2015头影X射线图像分析挑战的公共数据集[38]。该数据集由400个不同受试者的400张头颅侧位片组成,有19个标注的关键点。这些2D图像的大小为 1935 × 2400 1935 \times 2400 1935×2400,每个像素的物理分辨率为 0.1 × 0.1 0.1 \times 0.1 0.1×0.1mm。我们以 512 × 512 512\times512 512×512像素的输入/热力图目标尺寸设置网络。我们使用文献[38]中描述的训练/测试分割(150张训练,250张测试图像)和评估方法。我们对网络进行了30,000次迭代训练。由于Wang等人[38]提出的结果缺乏累积分布图,我们只比较了Ibragimov等人[28]和Lindner等人[17]的最佳表现方法的报告值。
如表4所示,我们提出的SCN优于先前获得该挑战胜利者的方法。与Lindner等人[17]在这个数据集上的表现相似,我们的结果表明,我们的方法在局部更准确( # O r \#O_r #Or与r=2mm),而对关键点错误识别的鲁棒性是相同的( # O r \#O_r #Or与r=4mm)。我们发现,在这个特别具有挑战性的数据集上,我们的方法的大部分问题都出现在解剖学上定义不明确的关键点上(例如,图4的C中下巴的前部关键点),如果没有手工图模型的强大几何约束,很难估计这些关键点的准确位置。这也可以从表4中比较其他方法在r=4mm的离群值方面的表现看出。随着误差半径的增加,Lindner等人[17]基于统计形状模型的变体的方法其性能也在增加,但仅从数据中学习几何约束的定位U-Net的性能增长却低于其他方法。
表4 来自2DSkull数据集的250张测试图像的定位结果,每幅图像包含19个关键点。我们根据Wang等人[38]的评估方法,报告了ISBI 2015大挑战的两个测试数据集的平均结果

4.4 脊柱CT (3DSpine)
为了将我们提出的SCN与其他最新的方法进行比较,我们还在公开的病理脊柱CT扫描的体积数据集[39]上进行了评估,该数据集用于MICCAI CSI 2014椎骨定位和识别挑战。该数据集包括各种挑战,如脊柱侧弯、椎骨骨折、金属插入物导致的严重图像伪影以及高度限制的视场。因此,由于脊柱 CT 扫描中局部外观的显著变化以及重复结构,必须学习关键点的空间配置以区分不同的椎骨。与先前报道的结果一致,我们将对这个数据集的评估分成两组。在第一组中,采用两折交叉验证评估挑战训练集的224张CT扫描片。在第二组中,网络在所有224张CT扫描片和额外18张CT扫描片上进行训练,并在由60张CT扫描片组成的挑战测试集中进行评估。平均体积大小为 512 × 512 × 160 512 \times 512 \times 160 512×512×160,体素分辨率为 0.34 × 0.34 × 2.06 0.34 \times 0.34 \times 2.06 0.34×0.34×2.06 mm 3。体卷积神经网络的输入和热力图目标大小为 96 × 96 × 192 96 \times 96 \times 192 96×96×192 体素;我们重新采样输入图像以使其具有每个维度的等距间隔为 2 毫米。有了这些输入尺寸,网络可以处理物理范围达 192 × 192 × 384 192\times192\times384 192×192×384毫米3的体积。由于一些体积在Z轴(即垂直于轴线的轴)上有较大的范围,因此无法适应网络,我们对这些体积进行如下处理。在训练期间,我们在Z轴的一个随机位置裁剪一个子体积。在测试过程中,我们将Z轴上的体积分成多个子体积,这些子体积有96个像素的重叠,并逐一进行处理。然后,我们通过取所有预测的最大响应来合并重叠的子体积的网络预测。网络结构与3DHand数据集的结构相同。我们对网络进行40,000次迭代训练。由于我们知道每个图像的物理体素分辨率,我们设置了归一化系数 s ( j ) s_{(j)} s(j)=1。
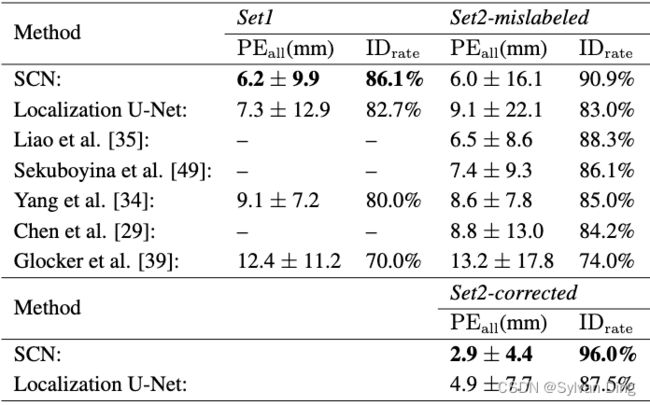
我们将我们的网络预测与这个高难度数据集的最新报告结果进行比较,见表5。在交叉验证集(Set1)和挑战测试集(Set2*)上,我们的方法优于在这个挑战数据集上评估的所有最先进的方法。尽管定位U-Net在这个数据集上显示出良好的结果,但无论是一般的关键点检测误差( P E a l l \mathrm{PE_{all}} PEall),还是对关键点错误识别的鲁棒性( I D r a t e \mathrm{ID_{rate}} IDrate),都不如我们的SCN好。由于缺乏对关键点空间配置的明确建模,定位U-Net在Set2中的 I D r a t e \mathrm{ID_{rate}} IDrate明显下降了8.5%. 与随机森林[39]和其他CNN[29,34,35]相比,我们的SCN执行热力图回归显示了最佳的定位性能。在Sekuboyina等人[49]的最新工作中,作者提出将脊柱解剖的三维信息投射到二维矢状面和冠状面,并仅使用这些视图作为他们的CNN的输入。虽然他们的方法是为脊柱数据集量身定做的,其中关键点位于与轴正交的轴上,但我们的通用SCN直接处理3D信息,超过了他们的方法。总的来说,我们表明我们的SCN优于所有最先进的方法,不需要复杂的训练程序[35]或前/后处理[34]。
Set2*:在测试数据集上评估我们提出的算法时,我们发现有三个体积图像的所有真实椎骨标签都被移动了多达五个椎骨,导致错误的关键点位置与实际位置有超过100毫米误差。为了与之前报道的结果进行比较,我们展示了原始数据集(Set2-mislabeled)的结果。与挑战赛组织者达成一致,我们也报告了更正后正确数据集(Set2-corrected)的结果,而组织者也相应地更新了挑战赛数据集。
表5 在3DSpine数据集上的定位结果,每个体积图像最多有26个关键点。 我们报告了224张图像的两折交叉验证结果(Set1)和60张图像的MICCAI CSI 2014挑战赛测试集(Set2)。对于Set2,我们报告了在未经修改的测试集上的结果,该Set2和测试集均存在被错误标记的椎骨(Set2-mislabeled),我们纠正了这些错误标记的椎骨(Set2-corrected)。*
5 讨论和结论
在本文中,我们表明,通过将空间配置纳入基于CNN的深度学习架构,对关键点检测的热力图进行回归,即使在训练数据集有限的情况下,我们也能实现高定位性能。我们在四个尺寸有限的数据集上评估了我们提出的SCN方法的定位性能,这些数据集包含不同解剖结构的二维X光片和三维MRI和CT,证明了我们提出的方法是普遍适用的。我们的结果表明,当对43个手部MRI体积图(第4.2节)、112个脊柱CT图像(第4.4节)、150个头颅侧位X光片(第4.3节)或600个手部X光片(第4.1节)进行训练时,我们的方法优于最先进的方法。在第4.1.2节中,我们特意将2DHand的训练图像限制在10张的极低数量,当对第4.1.1节中的相同图像(即2DHandFull)进行评估时,我们提出的网络仍然取得了与最先进方法相媲美的结果。
受限制关键点配置的解剖学约束的启发,我们的SCN方法自动从训练数据中学习到了关键点相对位置的约束,并将其整合到其空间配置组件中。以先前的最先进医学图像分析方法[17,23]将外观特征和类似解剖约束的手工模型分别引入到不同的组件中。在文献[27]中,我们展示了一种在单个随机森林框架中学习将外观信息和几何配置自动整合在一起的方法。然而,与所有这些以前的方法不同的是,这些方法要求两个独立的组件按顺序进行训练,它们之间没有任何互动,在我们的端到端训练的SCN中,局部外观和空间配置组件同时被优化,共同提供对关键点错误识别的高鲁棒性,以及在每个识别的关键点上的高准确性。
通过同时优化这两个组件,关键点检测的问题被分离成两个更简单的子问题,可以从低量的训练数据中建模,正如我们的实验所示。只有当回归目标(通过两个网络组件的输出相乘计算)在单一过程中以端到端方式进行优化时,这样的简化才有可能实现。这与Tompson等人[15]和Pfister等人[32]的方法不同,他们的每个网络组件都必须同时具有局部准确性和对错误识别的鲁棒性。需要注意的是,当(4)中给出的乘法被额外的卷积层取代时,正如Pfister等人[32]用于视频中的人类姿势估计,这并没有简化定位问题,因此仍然需要大量的训练数据。此外,我们提出的网络架构学会了将局部外观组件用于产生局部准确的候选预测,不需要区分局部类似的结构,而空间配置组件只专注于消除模糊性以提高对关键点错误识别的鲁棒性,不需要局部准确(见图9)。尽管没有理论保证优化过程将导致这种分离,但我们在所有的实验中都观察到了这种行为,我们在第4.1.3节中对2DHandFull实验进行了更详细的说明。
受最近全卷积U-Net[41]在分割问题上的成功启发,我们将这一架构调整为使用热力图回归的关键点检测。在广泛调整该任务后,我们的定位U-Net在实验中取得了有竞争力的定位性能,通常仅被我们提出的SCN超越。然而,仅就关键点错误识别鲁棒性进行评估时,定位U-Net并未展示出最先进的结果。这一点在3DSpine实验中尤其明显,因为该实验有很大的解剖和病理变化,我们的SCN在 I D r a t e \mathrm{ID_{rate}} IDrate评估中要比定位U-Net高出8.5%. 我们认为这种性能的下降是由于多尺度定位U-Net架构没有使用关键点在图像空间中不均匀分布的先验知识,而是受到其他解剖关键点的限制。因此,如果没有关于空间配置存在这种约束的先验知识,定位U-Net需要大量的训练数据,以仅从数据中学习这些多尺度的约束。这可以从3DSpine和2DHandReduced实验中最好地看出,我们提出的SCN在从有限的训练数据中学习相同的解剖变化时受益于这种先验知识。
当将我们的SCN与其他最先进的方法进行比较时,在我们的两个内部数据集2DHandFull和3DHand上,我们的表现优于之前的所有基于随机森林的结果[24,25,27],以及我们基于CNN的初步结果[33]。此外,在2DHandFull数据集上,我们显示出比目前最先进的基于Lindner等人[17]的随机森林的定位方法更好的结果,他们在相同的交叉验证分割上应用了我们标注的关键点。在2DSkull数据集上,我们的表现也超过了两位挑战赛的获胜者Lindner等人[17]以及Ibragimov等人[48]。对于3DSpine,Chen等人[29]同时使用随机森林和CNN预测,与Glocker等人[39]的纯随机森林方法相比,结果明显改善。Yang等人[34]只使用CNN的复杂方法也得到了类似的结果。最近,他们都被为这个数据集高度定制的CNN方法所超越[35,49]。然而,在这个具有挑战性的数据集上,我们的SCN在关键点检测误差方面优于所有这些方法,而不需要复杂或定制的实现。
总之,我们已经展示了如何将局部外观和空间配置的信息结合到一个单一的端到端训练网络中,用于解剖学关键点的定位。我们的通用架构不需要任何后处理步骤就能在不同的2D和3D数据集上取得最先进的关键点检测误差结果,即使是在训练图像数量有限的情况下。在未来的工作中,我们打算将我们的SCN与最近提出的Attention U-Net[50]进行比较,后者在抑制分割任务的无关特征方面具有一些相似性。此外,我们目前正在研究将我们的SCN扩展到关于遮挡结构和多物体定位,并将我们的SCN调整为语义分割问题(有关初步结果,请参见文献[51]),在该问题中,结构约束可能以类似的方式使用。
致谢
我们感谢所有四位匿名审稿人的全面工作和精彩评论,他们帮助我们改进了我们的手稿。此外,我们感谢Claudia Lindner在我们的2DHand数据集上应用他们的算法,感谢Thomas Ebner协助我们对数据集进行标注。我们感谢NVIDIA公司的支持,捐赠了本研究中使用的Titan Xp GPU。这项工作得到了奥地利科学基金(Austrian Science Fund,FWF)的支持:P28078-N33。
参考文献
[1] Beichel R, Bischof H, Leberl F, et al. Robust active appearance models and their application to medical image analysis[J]. IEEE transactions on medical imaging, 2005, 24(9): 1151-1169.
[2] Heimann T, Meinzer H P. Statistical shape models for 3D medical image segmentation: a review[J]. Medical image analysis, 2009, 13(4): 543-563.
[3] Johnson H J, Christensen G E. Consistent landmark and intensity-based image registration[J]. IEEE transactions on medical imaging, 2002, 21(5): 450-461.
[4] Urschler M, Zach C, Ditt H, et al. Automatic point landmark matching for regularizing nonlinear intensity registration: Application to thoracic CT images[C]//Medical Image Computing and Computer-Assisted Intervention–MICCAI 2006: 9th International Conference, Copenhagen, Denmark, October 1-6, 2006. Proceedings, Part II 9. Springer Berlin Heidelberg, 2006: 710-717.
[5] Štern D, Likar B, Pernuš F, et al. Parametric modelling and segmentation of vertebral bodies in 3D CT and MR spine images[J]. Physics in Medicine & Biology, 2011, 56(23): 7505.
[6] Cootes T F, Taylor C J, Cooper D H, et al. Active shape models-their training and application[J]. Computer vision and image understanding, 1995, 61(1): 38-59.
[7] Felzenszwalb P F, Huttenlocher D P. Pictorial structures for object recognition[J]. International journal of computer vision, 2005, 61: 55-79.
[8] LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324.
[9] LeCun Y, Bengio Y, Hinton G. Deep learning[J]. nature, 2015, 521(7553): 436-444.
[10] Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90.
[11] He K, Zhang X, Ren S, et al. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification[C]//Proceedings of the IEEE international conference on computer vision. 2015: 1026-1034.
[12] Cireşan D C, Giusti A, Gambardella L M, et al. Mitosis detection in breast cancer histology images with deep neural networks[C]//Medical Image Computing and Computer-Assisted Intervention–MICCAI 2013: 16th International Conference, Nagoya, Japan, September 22-26, 2013, Proceedings, Part II 16. Springer Berlin Heidelberg, 2013: 411-418.
[13] Sirinukunwattana K, Pluim J P W, Chen H, et al. Gland segmentation in colon histology images: The glas challenge contest[J]. Medical image analysis, 2017, 35: 489-502.
[14] Zheng S, Jayasumana S, Romera-Paredes B, et al. Conditional random fields as recurrent neural networks[C]//Proceedings of the IEEE international conference on computer vision. 2015: 1529-1537.
[15] Tompson J J, Jain A, LeCun Y, et al. Joint training of a convolutional network and a graphical model for human pose estimation[J]. Advances in neural information processing systems, 2014, 27.
[16] Liu D, Zhou K S, Bernhardt D, et al. Search strategies for multiple landmark detection by submodular maximization[C]//2010 IEEE computer society conference on computer vision and pattern recognition. IEEE, 2010: 2831-2838.
[17] Lindner C, Bromiley P A, Ionita M C, et al. Robust and accurate shape model matching using random forest regression-voting[J]. IEEE transactions on pattern analysis and machine intelligence, 2014, 37(9): 1862-1874.
[18] Breiman L. Random forests[J]. Machine learning, 2001, 45: 5-32.
[19] Ibragimov B, Likar B, Pernus F. A game-theoretic framework for landmark-based image segmentation[J]. IEEE Transactions on Medical Imaging, 2012, 31(9): 1761-1776.
[20] Toews M, Arbel T. A statistical parts-based model of anatomical variability[J]. IEEE Transactions on Medical Imaging, 2007, 26(4): 497-508.
[21] Glocker B, Feulner J, Criminisi A, et al. Automatic localization and identification of vertebrae in arbitrary field-of-view CT scans[C]//Medical Image Computing and Computer-Assisted Intervention–MICCAI 2012: 15th International Conference, Nice, France, October 1-5, 2012, Proceedings, Part III 15. Springer Berlin Heidelberg, 2012: 590-598.
[22] Potesil V, Kadir T, Platsch G, et al. Personalized graphical models for anatomical landmark localization in whole-body medical images[J]. International Journal of Computer Vision, 2015, 111: 29-49.
[23] Donner R, Menze B H, Bischof H, et al. Global localization of 3D anatomical structures by pre-filtered Hough Forests and discrete optimization[J]. Medical image analysis, 2013, 17(8): 1304-1314.
[24] Štern D, Ebner T, Urschler M. From local to global random regression forests: exploring anatomical landmark localization[C]//Medical Image Computing and Computer-Assisted Intervention–MICCAI 2016: 19th International Conference, Athens, Greece, October 17-21, 2016, Proceedings, Part II 19. Springer International Publishing, 2016: 221-229.
[25] Ebner T, Stern D, Donner R, et al. Towards automatic bone age estimation from MRI: localization of 3D anatomical landmarks[C]//Medical Image Computing and Computer-Assisted Intervention–MICCAI 2014: 17th International Conference, Boston, MA, USA, September 14-18, 2014, Proceedings, Part II 17. Springer International Publishing, 2014: 421-428.
[26] Criminisi A, Robertson D, Konukoglu E, et al. Regression forests for efficient anatomy detection and localization in computed tomography scans[J]. Medical image analysis, 2013, 17(8): 1293-1303.
[27] Urschler M, Ebner T, Štern D. Integrating geometric configuration and appearance information into a unified framework for anatomical landmark localization[J]. Medical image analysis, 2018, 43: 23-36.
[28] Russakovsky O, Deng J, Su H, et al. Imagenet large scale visual recognition challenge[J]. International journal of computer vision, 2015, 115: 211-252.
[29] Chen H, Shen C, Qin J, et al. Automatic localization and identification of vertebrae in spine CT via a joint learning model with deep neural networks[C]//Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part I 18. Springer International Publishing, 2015: 515-522.
[30] Zhang J, Liu M, Shen D. Detecting anatomical landmarks from limited medical imaging data using two-stage task-oriented deep neural networks[J]. IEEE Transactions on Image Processing, 2017, 26(10): 4753-4764.
[31] Toshev A, Szegedy C. Deeppose: Human pose estimation via deep neural networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2014: 1653-1660.
[32] Pfister T, Charles J, Zisserman A. Flowing convnets for human pose estimation in videos[C]//Proceedings of the IEEE international conference on computer vision. 2015: 1913-1921.
[33] Payer C, Štern D, Bischof H, et al. Regressing heatmaps for multiple landmark localization using CNNs[C]//Medical Image Computing and Computer-Assisted Intervention–MICCAI 2016: 19th International Conference, Athens, Greece, October 17-21, 2016, Proceedings, Part II 19. Springer International Publishing, 2016: 230-238.
[34] Yang D, Xiong T, Xu D, et al. Automatic vertebra labeling in large-scale 3D CT using deep image-to-image network with message passing and sparsity regularization[C]//Information Processing in Medical Imaging: 25th International Conference, IPMI 2017, Boone, NC, USA, June 25-30, 2017, Proceedings 25. Springer International Publishing, 2017: 633-644.
[35] Liao H, Mesfin A, Luo J. Joint vertebrae identification and localization in spinal CT images by combining short-and long-range contextual information[J]. IEEE transactions on medical imaging, 2018, 37(5): 1266-1275.
[36] Ghesu F C, Georgescu B, Grbic S, et al. Towards intelligent robust detection of anatomical structures in incomplete volumetric data[J]. Medical image analysis, 2018, 48: 203-213.
[37] Ghesu F C, Georgescu B, Zheng Y, et al. Multi-scale deep reinforcement learning for real-time 3D-landmark detection in CT scans[J]. IEEE transactions on pattern analysis and machine intelligence, 2017, 41(1): 176-189.
[38] Wang C W, Huang C T, Lee J H, et al. A benchmark for comparison of dental radiography analysis algorithms[J]. Medical image analysis, 2016, 31: 63-76.
[39] Glocker B, Zikic D, Konukoglu E, et al. Vertebrae localization in pathological spine CT via dense classification from sparse annotations[C]//Medical Image Computing and Computer-Assisted Intervention–MICCAI 2013: 16th International Conference, Nagoya, Japan, September 22-26, 2013, Proceedings, Part II 16. Springer Berlin Heidelberg, 2013: 262-270.
[40] Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2015: 3431-3440.
[41] Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation[C]//Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18. Springer International Publishing, 2015: 234-241.
[42] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.
[43] Srivastava N, Hinton G, Krizhevsky A, et al. Dropout: a simple way to prevent neural networks from overfitting[J]. The journal of machine learning research, 2014, 15(1): 1929-1958.
[44] Maas A L, Hannun A Y, Ng A Y. Rectifier nonlinearities improve neural network acoustic models[C]//Proc. icml. 2013, 30(1): 3.
[45] Nesterov Y E. A method of solving a convex programming problem with convergence rate O ( k ∧ 2 ) O\bigl(k^{\wedge}2\bigr) O(k∧2)[C]//Doklady Akademii Nauk. Russian Academy of Sciences, 1983, 269(3): 543-547.
[46] Lindner C, Wang C W, Huang C T, et al. Fully automatic system for accurate localisation and analysis of cephalometric landmarks in lateral cephalograms[J]. Scientific reports, 2016, 6(1): 33581.
[47] Štern D, Payer C, Lepetit V, et al. Automated age estimation from hand MRI volumes using deep learning[C]//Medical Image Computing and Computer-Assisted Intervention–MICCAI 2016: 19th International Conference, Athens, Greece, October 17-21, 2016, Proceedings, Part II. Cham: Springer International Publishing, 2016: 194-202.
[48] Ibragimov B, Likar B, Pernuš F, et al. Shape representation for efficient landmark-based segmentation in 3-D[J]. IEEE transactions on medical imaging, 2014, 33(4): 861-874.
[49] Sekuboyina A, Rempfler M, Kukačka J, et al. Btrfly net: Vertebrae labelling with energy-based adversarial learning of local spine prior[C]//Medical Image Computing and Computer Assisted Intervention–MICCAI 2018: 21st International Conference, Granada, Spain, September 16-20, 2018, Proceedings, Part IV 11. Springer International Publishing, 2018: 649-657.
[50] Oktay O, Schlemper J, Folgoc L L, et al. Attention u-net: Learning where to look for the pancreas[J]. arXiv preprint arXiv:1804.03999, 2018.
[51] Payer C, Štern D, Bischof H, et al. Multi-label whole heart segmentation using CNNs and anatomical label configurations[C]//Statistical Atlases and Computational Models of the Heart. ACDC and MMWHS Challenges: 8th International Workshop, STACOM 2017, Held in Conjunction with MICCAI 2017, Quebec City, Canada, September 10-14, 2017, Revised Selected Papers. Cham: Springer International Publishing, 2018: 190-198.
❤️ 如果你喜欢我的文章,可以通过点赞和收藏支持我。更多内容欢迎关注我的博客:https://blog.csdn.net/IYXUAN
https://www.github.com/christianpayer/ ↩︎
www.ipilab.org/BAAweb ↩︎
