MCMC算法原理及其实例
一.概述
通过概率统计模拟来进行数值计算的方法统称为蒙特卡罗(Monte Carlo)方法，而MCMC方法称为马尔科夫链蒙特卡洛(Markov Chain Monte Carlo)方法。显然，MCMC法为MC法的一种特例。MCMC法是利用马尔可夫链的细致平衡条件进行采样，再通过所采样的样本进行数值计算的一种方法。
二.实例
下面将介绍三个利用MC方法的实例，分别为
（1）对圆周率
进行数值计算
（2）求解定积分的数值解
（3）由重要采样法求解定积分的数值解
1.对圆周率进行数值计算
设某二维均匀分布U的正概率密度区域是边长为2的正方形，如下图所示
该正方形的内切圆已在图中标红，假设向该正方形内均匀的撒一把豆子，理想情况下，豆子落入红圆内的概率为
其中m为总豆子数，n为落入红圆内的豆子数。显然，本次撒豆子的行为服从二维均匀分布U，因此，又可以得到
从而有
不难发现，通过撒豆子(生成均匀分布随机数)，便可计算出的数值，这个方法便是MC方法的一个简单例子，有大数定律可知，撒的豆子越多，所求得的值便越精确，下面将利用MATLAB编程对上述过程进形模拟，程序如下
%在正方形内生成均匀分布随机数，即撒豆子
N=1e4;
x=unifrnd(-1,1,1,N);
y=unifrnd(-1,1,1,N);
z=x(x.^2+y.^2<=1);%找出落入内切圆内以及圆上的豆子
p=4*length(z)/length(x);%计算pi值
err=(p-pi)/pi*100;%计算相对误差
%绘图
hold on
for i=1:length(x)
if x(i)^2+y(i)^2<=1
plot(x(i),y(i),'.r')
else
plot(x(i),y(i),'.b')
end
end
title('样本点分布图');
axis square;
hold off
fprintf('pi值为%1.4f，相对误差为%1.6f\n',p,err);%显示结果【注】 为了计算速度，该程序只生成了1e4个样本点，样本点越多结果越精确。
运行结果如下
2.求解定积分的数值解
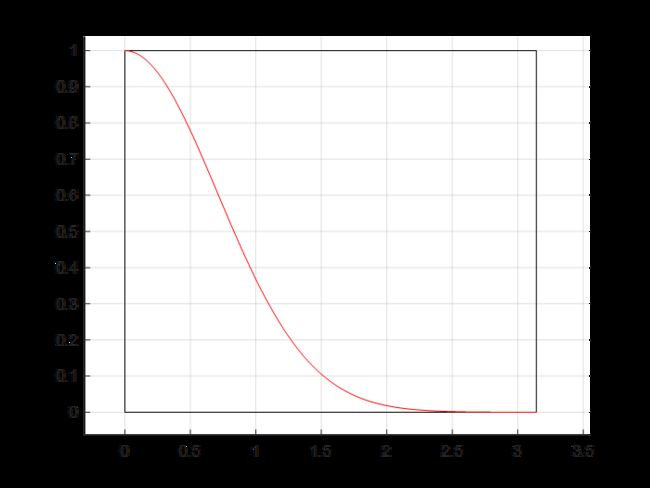
由实例1不难发现MC方法的一个基本思想，即利用样本量足够大的古典概型与几何概型建立等式，进而求得等式中未知参数的数值解，因几何概型涉及到面积之比，并且定积分的数值解也是一个面积，故利用上述思想亦能对定积分进行求解。以如下定积分为例
显然，被积函数在[0,]上的最大值为1，因此撒豆子的区域为
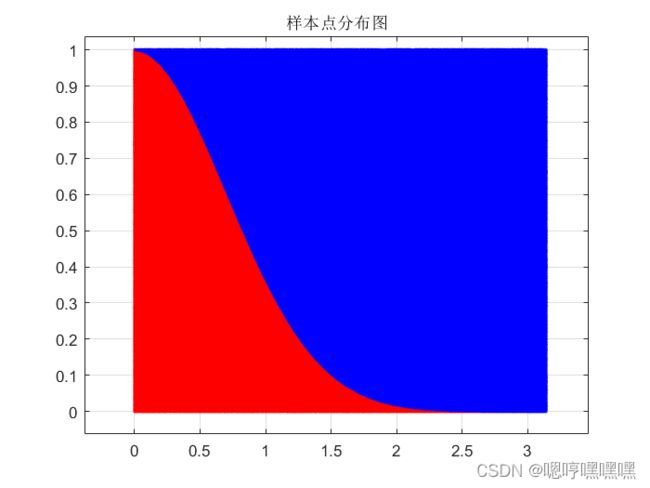
如下图所示，设m为豆子总数，n为落入红色曲线(被积函数)以下豆子的数量
则待求积分值为
下面将利用MATLAB编程对上述过程进形模拟，程序如下
%在矩形目标区域内撒豆子
x=unifrnd(0,pi,1,1e6);
y=rand(1,1e6);
%定义被积函数并找出落入被积函数曲线以下的豆子
f=@(x)exp(-x.^2);
lg=y<=f(x);
xx=x(lg);xxf=x(~lg);
yy=y(lg);yyf=y(~lg);
inti=pi*length(xx)/length(x); %求解积分值
zjb=integral(f,0,pi); %求解真值
err=(inti-zjb)/zjb*100; %计算相对误差
%绘制样本点分布图
hold on
scatter(xx,yy,'.r')
scatter(xxf,yyf,'.b')
title('样本点分布图');
grid on;box on;
hold off
fprintf('积分值为%1.4f，相对误差为%1.6f\n',inti,err); %显示结果运行结果如下
3.由重要采样法求解定积分的数值解
实例1,2介绍了MC方法的一个基本思想，接下来将通过该实例介绍另一种思想——通过重要采样法求解定积分的数值解
重要采样(Importance sampling)法概述：
因此，可由如下过程计算函数f(x)的积分值
下面将通过MATLAB利用上述方法计算定积分
MATLAB程序如下
%定义q(x）
syms x;
q1=3*x.^2;
q=@(x)double(subs(q1,x));
%定义q(x）的原函数Q(x)
Q=@(x)double(subs(finverse(int(q1)),x));
%利用Q(x)对q(x)进行采样，采样结果为z，采样数量为2e4
r=rand(1,2e4);
z=Q(r);
f=@(x)sin(x);%定义被积函数
F=@(x)f(x)./q(x);%定义随机变量的函数
jg=mean(F(z));%求取均值，即积分值
zjg=integral(f,0,1);%求取真值
err=(jg-zjg)/zjg*100;%求取相对误差
fprintf('积分值为%1.4f，相对误差为%1.6f\n',jg,err); %显示结果运行结果如下
三.采样方法（这里仅是对下述采样方法的概括，文献[1]中有对各个采样方法的详细说明）
通过上述简单实例不难发现，MC法需要对某个目标分布进行抽样，上述实例中的目标分布均为常见的一维分布，采样方法较为简单，如实例3使用的是概率分布采样（利用均匀分布U(0,1)对CDF的反函数进行采样），但在目标分布较为复杂的情况下，可利用马尔可夫链的细致平衡条件进行采样，基于此种采样的MC法，称为MCMC方法。
下面将介绍三种采样方法
（1）拒绝采样
（2）M-H采样
（3）Gibbs采样
其中（2）和（3）为基于马尔可夫链的采样法。
1.拒绝采样(reject sampling)
通过建议分布(proposed distribution)q(x),q(x)的CDF应方便求得,构造接受α=f(x)/(mq(x)),其中f(x)为目标分布的概率密度函数，m为一个常数，目的是保证f(x)≤mq(x)，由于M-H法是该方法的改良版，故不对该采样方法进行编程操作，该方法的伪代码[1]如下
2.M-H采样(用于对一维分布进行采样)
该方法的思路与拒绝采样类似，均构造了接受率，但M-H采样是利用马尔可夫链细致平衡条件(i)P(i,j)=(j)p(j,i)对接受率进行构造，具体过程如下
对于细致平衡条件(i)P(i,j)=(j)P(j,i)，引入随机矩阵Q，使得
P(j,i)=Q(i,j)
(i,j)
从而有
(i)Q(i,j)(i,j)=(j)Q(j,i)(j,i)
则
(i,j)= (j)Q(j,i)
该方法将对随时间前进的随机矩阵Q采样，所采样本被保留下来的概率为，在M-H方法中，为了使采样效率相对较高(避免接受率长时间过小)，采用如下接受率公式
下面将通过MATLAB对M-H采样进行编程,采样分布的核密度为p(x),随机矩阵为q(x),接受率为.
伪代码如下
MATLAB代码如下
x(1)=0;%样本初始值
N=2e5;%采样次数
p=@(x)0.3*exp(-0.2*x.^2)+0.7*exp(-0.2*(x-10).^2); %p(x)的核密度，采样过程中目标分布PDF中的常数会被消去，因此用核密度即可。
%进行M-H采样
for i=1:N-1
xs=normrnd(x(i),10);%生成候选样本
pxs=p(xs);%计算该候选样本处的核密度值
px=p(x(i));%计算上一个已采样本处的核密度值
qxs=normpdf(xs,x(i),10);%计算在上一个已采样本条件下，该候选样本处随机矩阵q的概率密度值
qx=normpdf(x(i),xs,10);%计算在该候选样本条件下，上一个已采样本处随机矩阵q的概率密度值
alpha=min(pxs*qx/(px*qxs),1);%计算接受率
%按接受率判断是否接受该候选样本
u=rand;
if u<=alpha
x(i+1)=xs;
else
x(i+1)=x(i);
end
end
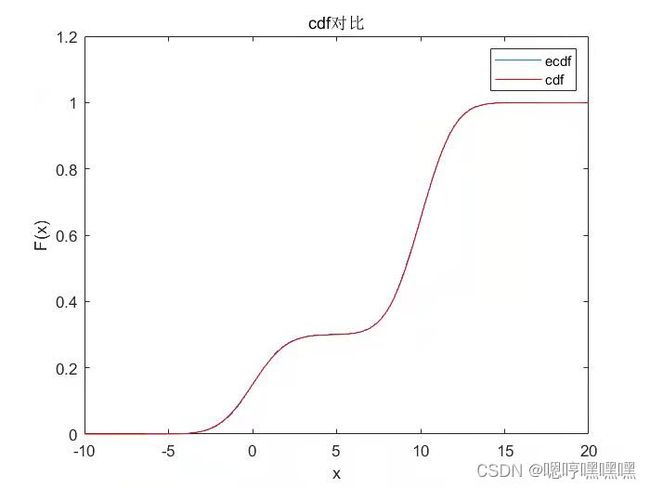
%绘制各类对比图像，对采样结果进行分析
xx=-10:0.01:20;
fp=p(xx);
A=sum(fp)*0.01;%A=integral(p,-inf,inf),p是核概率密度函数，下面fp/A的目的是使积分为1，求出pdf。
hold on
ecdf(x);
c=linspace(-10,20,1000);
for i=1:length(c)
F(i)=integral(@(x)p(x)/A,-inf,c(i));
end
plot(c,F,'r')
legend('ecdf','cdf')
title('cdf对比')
[ni,bin]=histcounts(x);
binx=bin(2)-bin(1);
hold off
figure
hold on
bar((bin(1)+bin(2))/2:binx:(bin(end-1)+bin(end))/2,ni/N/binx)
plot(xx,fp/A,'r')
hold off
legend('采样','目标分布')
title('pdf对比1')
figure
hold on
ksdensity(x)
plot(xx,fp/A,'r')
title('pdf对比2')
legend('采样','目标分布')
hold off运行结果如下
3.Gibbs采样（用于对2维及2维以上分布进行采样）
该方法的思路与M-H类似，但接受率恒为1，具体数学推导可查阅文献[1]，其伪代码如下
MATLAB程序如下
%% 该程序将利用Gibbs采样二维正态分布
%样本初始化
N=3000; %采样数量
mu=[0,0]; %目标分布均值
rho=[0.8,0.8]; %目标分布相关系数p21与p12
Sigma=[1,0.8;0.8,1];%目标分布方差与相关系数矩阵
%确定采样区域
low=[-3,-3];%采样区域下限
up=[3,3];%采样区域上限，
x=zeros(N,2);%样本初始化（分配空间）,设第一列为x1，第二列为x2
%设置样本初始值
x(1,1)=unifrnd(low(1),up(1));
x(1,2)=unifrnd(low(2),up(2));
dims=1:2; %样本维度
%Gibbs程序
for t=2:N
T=[t-1,t];%为了给下面的均值以及方差公式代数而生成矩阵位置索引
for i=1:2 %采样维度
dim=dims~=i;%为了给下面的均值以及方差公式代数而生成的逻辑数组
mud=mu(i)+rho(i)*(x(T(i),dim)-mu(dim));%计算均值
vard=sqrt(1-rho(i)^2);%计算方差
x(t,i)=normrnd(mud,vard);%产生正态分布随机数
end
end
%绘制Gibbs采样的对比图像，分析采样效果
h1=scatter(x(:,1),x(:,2),'.r');
hold on;
for t = 1:30
h2=plot([x(t,1),x(t+1,1)],[x(t,2),x(t,2)],'k-');
plot([x(t+1,1),x(t+1,1)],[x(t,2),x(t+1,2)],'k-');
plot(x(t+1,1),x(t+1,2),'ko');
end
h3=scatter(x(1,1),x(1,2),'go','Linewidth',3);
legend([h1,h2,h3],'采样点','前30个样本点的采样路径','初始采样点','Location','Northwest')
hold off
title('采样情况图')
xlabel('x1');
ylabel('x2');
figure
xd=mvnrnd(mu,Sigma,5000);
subplot(1,3,1);scatter(xd(:,1),xd(:,2),'.r');
xlabel('x1');ylabel('x2');title('目标分布样本');
subplot(1,3,2);scatter(x(:,1),x(:,2),'.b');
xlabel('x1');ylabel('x2');title('Gibbs采样样本')
subplot(1,3,3);hold on
scatter(xd(:,1),xd(:,2),'.r');title('目标分布样本')
scatter(x(:,1),x(:,2),'.b');title('Gibbs采样样本')
xlabel('x1');ylabel('x2');title('两种样本对比');
hold off
xx1=low(1):0.01:up(1);
xx2=low(1):0.01:up(1);
[X,Y]=meshgrid(xx1,xx2);
Z=zeros(length(X),length(X));
for i=1:length(X)
for j=1:length(X)
Z(i,j)=mvnpdf([X(i,j),Y(i,j)],mu,Sigma);
end
end
figure
subplot(1,2,1);
scatter3(x(:,1),x(:,2),mvnpdf([x(:,1),x(:,2)],mu,Sigma),'.r');
xlabel('x1');ylabel('x2');zlabel('z');title('采样样本PDF');
subplot(1,2,2);
mesh(X,Y,Z);
xlabel('x1');ylabel('x2');zlabel('z');title('目标分布PDF');
figure
mesh(X,Y,Z);
hold on;
scatter3(x(:,1),x(:,2),mvnpdf([x(:,1),x(:,2)],mu,Sigma),'.r');
xlabel('x1');ylabel('x2');zlabel('z');title('两种样本对比');
hold off
rectangle('Position', [0,0,pi,1])
z=linspace(0,pi);
hold on
plot(z,f(z),'r');
grid on运行结果如下
四.参考文献
[1]An Introduction to MCMC for Machine Learning