【深度学习】日常笔记2

一直以来其实对调参这个词不太熟悉，后面知道了比如学习率就为超参数，是被调参的对象：

↑标量方程对向量的导数

大概就是↓

在对矩阵求导时，我们需要使用矩阵微积分中的求导法则。对于一个标量函数 f(x)，它关于向量 x 的导数可以表示为：

∂f(x) / ∂x = [∂f(x) / ∂x1, ∂f(x) / ∂x2, ..., ∂f(x) / ∂xn]

其中 xi 表示向量 x 中的第 i 个分量。

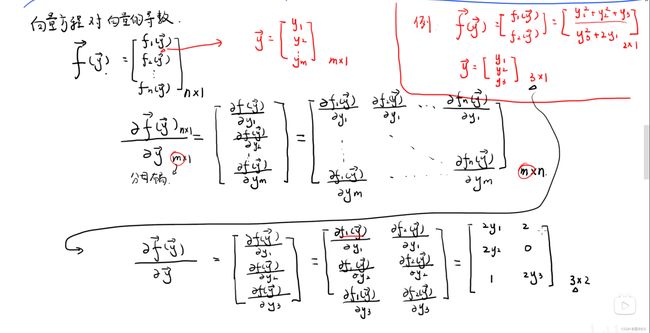
对于一个向量函数 f(x)，它关于向量 x 的导数可以表示为一个矩阵：

∂f(x) / ∂x = [∂f1(x) / ∂x1, ∂f1(x) / ∂x2, ..., ∂f1(x) / ∂xn; ∂f2(x) / ∂x1, ∂f2(x) / ∂x2, ..., ∂f2(x) / ∂xn; ... ∂fm(x) / ∂x1, ∂fm(x) / ∂x2, ..., ∂fm(x) / ∂xn]

这里放上实例：

这里是线性回归的解析解推导过程：

我们的目标是最小化损失函数 L(w) = ∥y - Xw∥^2，其中 y 是 n 维数据列向量，X 是 n * p 的特征矩阵，w 是 p 维权重列向量。

将损失函数展开，得到 L(w) = (y - Xw)⊤(y - Xw) = (y⊤ + (-Xw)⊤)(y - Xw) = y⊤y - 2w⊤X⊤y + w⊤X⊤Xw（v⊤u = u⊤v，其中 v 和 u 都是向量）

L(w)对 w 求导数，

其中，第一项 y⊤y 是常数，对 w 的偏导数为 0。

第二项可以应用矩阵求导法则，即：

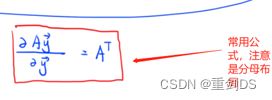
∂/∂w (-2w⊤X⊤y) = ∂/∂w (-2 y⊤Xw) ，根据下面的常用公式1↓

那么∂/∂w (-2w⊤X⊤y) = -2X⊤y

对于第三项∂/∂w (w⊤X⊤Xw)，我们也可以应用矩阵求导法则：

根据下面的常用公式2↓

注意是分母布局，X⊤X刚好是个对称矩阵，那结果就呼之欲出了，∂/∂w (w⊤X⊤Xw) = X⊤Xw + (X⊤X)⊤w = 2 X⊤Xw

结合以上三项，得到梯度 g(w) = -2X⊤y + 2X⊤Xw

令梯度为零，即 2X⊤Xw = 2X⊤y，解出 w 使得上式成立，得到：

w* = (X⊤X)^-1 X⊤y

其中 (X⊤X)^-1 表示 X⊤X 的逆矩阵。所以，最小化损失函数时，权重向量的解析解就是 w* = (X⊤X)^-1 X⊤y。

↑向量方程对向量的导数

如果是分子布局的话，对例子来说求导所得的矩阵就是2x3的矩阵了。

↑常用公式1

↑常用公式2

↑常用公式2的例子

学到这里，发现自己数学一的线性代数貌似不够用了…所以打算先去补下矩阵微积分的知识。

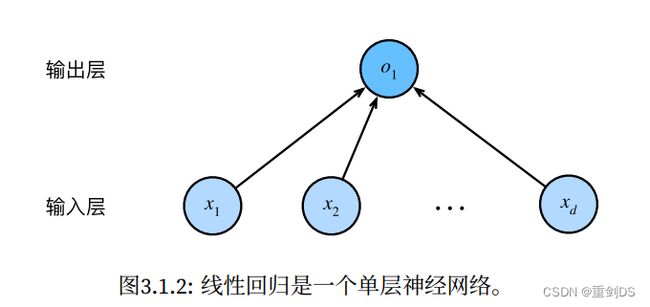
线性回归对应到神经网络图的话，这种每个输入都与每个输出相连，这种变换被称为全连接层。所以线性回归模型也是一个简单的神经网络。

做下p95的题目：

答：

1.

在最小化平方误差的问题中，我们要找到一个常数b，使得∑(xi − b)^2最小化。为了解决这个问题，可以先对该式进行展开：

∑(xi − b)^2 = ∑xi^2 - 2b∑xi + nb^2

对b求导数并令导数为0，有：

d/db(∑(xi − b)^2) = -2∑xi + 2nb = 0

解出b，有：

b = (x1 + x2 + ... + xn) / n

因此，最优值b的解析解为所有数据的平均值。

2.

这个问题与正态分布的关系在于，如果我们假设这些数据是从一个服从正态分布的总体中抽取出来的样本，并且忽略掉方差，则最小化 ∑(xi−b)2 的问题就等价于用最小二乘法估计这个正态分布总体的均值参数 μ 的问题。具体地说，最小化 ∑(xi−b)2 可以看作是寻找一个使误差平方和最小的 b，而这个 b 就等价于这个样本的均值 x̄。

在正态分布中，样本均值是对总体均值的一个无偏估计，而这个估计的方差与样本量 n 成反比，即随着样本量的增加，样本均值的估计精度会提高。

最小二乘法通过最小化残差平方和来确定输入变量与输出变量之间的线性关系，其中残差指的是观测值与估计值之间的差异。

因此在正态分布中，最小二乘法可以被用来估计均值参数 μ。具体地说，我们可以将最小化 ∑(xi−b)2 看作是寻找一个使误差平方和最小的 b，而这个 b 就等价于这个样本的均值x̄。

因此，最小化 ∑(xi−b)2 的问题就可以被视为用最小二乘法估计这个正态分布总体的均值参数 μ 的问题。

答：

要求负对数似然的最小值是因为原本的P(y | X)是要求最大的，毕竟是极大似然估计，但是优化通常都是说最小化而非最大化，所以求负对数似然-logPy X)的最小值其实就是求P(y | X)的最大罢了。

答：

1.

注意：，而yi=f(xi)+ ϵ，故ϵ=yi - f(xi)

数据的负对数似然为：

-log P(y|X) = -log ∏i=1^n P(yi|xi) = -∑i=1^n log P(yi|xi)

= -∑i=1^n log (1/2 exp(-|yi-f(xi)|))

= ∑i=1^n |yi-f(xi)| + n log 2

2.

要求模型的最小化损失函数，可以通过最小化负对数似然得到。将负对数似然代入后，有：

L(f) = ∑i=1^n |yi - f(xi)| + n log 2

对L(f)求导得到梯度G(f)，为：

G(f) = -∑i=1^n sign(yi - f(xi))

sign函数是一个符号函数，其定义如下：

当x>0时，sign(x)=1； 当x=0时，sign(x)=0； 当x<0时，sign(x)=-1。

将G(f)设置为0，解出f的解析解：

f(x) = median(y1, y2, ..., yn)

median(y1, y2, ..., yn)为所有y1, y2, ..., yn的中位数

3.

随机梯度下降算法可以如下实现：

1）初始化 f_0

2）对于每个epoch：

a) 打乱数据集 X 和 y 的顺序

b) 对于每个样本 (xi, yi)，计算梯度 G_i(f) = sign(yi - f(xi))

c) 更新模型参数：f_{t+1} = f_t - η G_i(f_t)，其中 η 是学习率

3）重复步骤2直至收敛

在驻点附近可能会出现振荡或者停滞的情况，这是因为梯度下降算法在该点的梯度接近0，导致更新时只有微小的变化，难以跳出该驻点。解决这个问题可以采用一些改进的方法，例如动量、自适应学习率等。另外，在噪声较大的情况下，模型可能会过度拟合噪声，导致性能下降，需要使用正则化等方法来缓解。

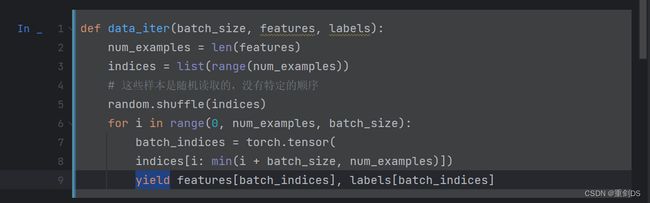
学习的时候发现了py中的yield这个关键字。p97

yield 关键字用于暂停（挂起）函数并返回一个值给调用者，而不会终止该函数。在这种情况下，使用yield关键字可以将批量大小分割为一小部分，并逐个迭代这些小部分，以便能够处理大型数据集，而无需将整个数据集存储在内存中。

每次调用生成器时，它从上次离开的地方恢复，并继续运行然后从yield语句返回下一批数据，这些数据将被传递给调用者。当没有更多数据可供产生时，该函数会正常退出。

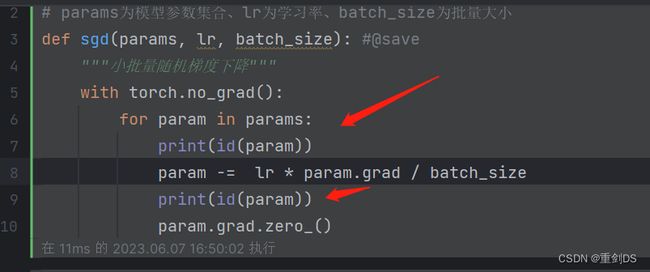
# 定义优化函数
# params为模型参数集合、lr为学习率、batch_size为批量大小

# SGD（Stochastic Gradient Descent）是一种随机梯度下降算法
def sgd(params, lr, batch_size): #@save
    """⼩批量随机梯度下降"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

with torch.no_grad()上下文管理器包装的代码块内的操作不会被记录梯度信息。这个上下文管理器的作用是临时关闭PyTorch中的自动求导机制，以减少内存消耗并加速计算。在这种情况下，即使执行了需要梯度的操作，也不会构建计算图，因此也就不会对变量进行求导。这对于评估模型或者进行推理时非常有用。

在使用反向传播算法计算梯度时，梯度是会累加的，而不是被替换掉。因此，在每次更新模型参数之前需要将累积的梯度清零，以避免出现重复计算或错误更新的情况。param.grad.zero_()就是用来实现这个功能的。它将参数的梯度设置为0，以便下一次迭代计算新的梯度。

在训练过程中，发现了一个BUG，原因貌似是因为
param -= lr * param.grad / batch_size和param =param  -  lr * param.grad / batch_size的区别。一开始写成第二个了。

所以报错：AttributeError: 'NoneType' object has no attribute 'zero_'

后面貌似发现原因了↓

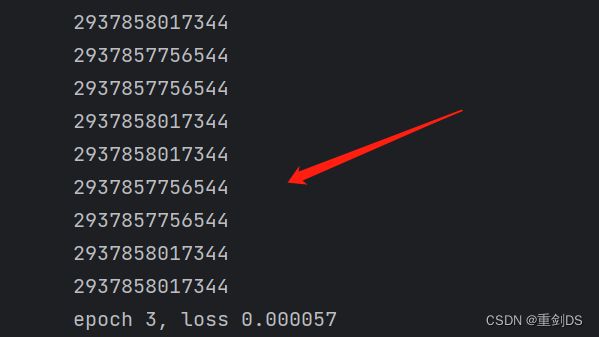
在SGD函数中，我们使用param = param - lr * param.grad / batch_size这一行代码来更新每个参数。但是，在这个语句中，赋值运算符（=）会将右侧的计算结果分配给变量param，这将创建一个新的Tensor对象并将其分配给变量param，而不是原始的Tensor对象。因此，当我们调用param.grad.zero_()时，它实际上操作的是副本的属性grad，并没有对原始参数对象进行修改。而且，由于我们在函数中只是更新了副本的值，而不是原始对象的值，因此即使我们在函数中执行了零梯度操作，也不会直接影响到原始参数对象的grad属性。

当我们将 param = param - lr * param.grad / batch_size 改为 param -= lr * param.grad / batch_size 后，赋值运算符 -= 将使用减法运算符（-）和赋值运算符（=）组合成一个复合运算符（-=），这意味着 param -= lr * param.grad / batch_size 等价于 param = param - lr * param.grad / batch_size。这个复合运算符是原位(in-place)更新操作，可以直接修改原始对象的值，所以在调用param.grad.zero_()时就不会出现错误了。

通过↑打印前后地址即可证明。

p101的练习↓

答：这个问题其实也可以说“将权重都设置为1的话，合理吗？”。
其实都是不合理的，因为无论是将所有权重都初始化为0或1，则会破坏权重之间的不对称性，导致每个神经元输出相同的值。这种情况下，网络中的每个层将执行相同的功能，并且在进行反向传播时，每个权重都会获得相同的更新值，因此神经网络无法学习输入数据中的复杂模式，并且无法收敛到最优解。
所以应该使用其他更好的方法来初始化权重，如随机初始化或Xavier初始化，以确保权重之间有不对称性，并且神经网络能够有效地学习和训练。

答：计算二阶导数时可能会遇到以下问题：

1. 计算量大：计算高阶导数需要进行多次求导，每次都要重新计算并更新中间变量，因此计算量较大，尤其是在深度神经网络中。

2. 数值稳定性：在计算较高阶的导数时，由于存在舍入误差和数值不稳定性，可能导致结果不准确，并且误差会随着求导次数的增加而放大。

3. 内存消耗：在计算高阶导数时，需要存储更多的中间变量，以便在反向传播时使用。这可能会导致内存消耗过大，特别是在处理大规模数据集时。

为了克服这些问题，可以采用以下方法：

1. 通过符号计算来计算导数：符号计算可以直接对表达式进行求导，而无需计算数值。这种方法可以有效地减少计算量，并且可以得到精确的结果，但是它需要额外的计算时间和存储空间。

2. 利用自动微分工具：自动微分是一种自动计算导数的技术，它结合了符号计算和数值计算，可以非常快速地计算高阶导数。现代深度学习框架如PyTorch和TensorFlow都内置了自动微分功能，可以帮助开发人员方便地计算梯度和高阶导数。

3. 使用近似方法：在某些情况下，可以使用一些近似方法来计算高阶导数。例如，Hessian矩阵（海森矩阵、黑塞矩阵）可以通过有限差分法进行近似。这种方法计算简单，但可能存在数值误差和计算效率低的问题。

总之，在实际应用中，我们需要根据具体情况选择合适的方法来计算高阶导数，并在计算量、数值稳定性和内存消耗之间进行权衡。

7. 如果样本个数不能被批量⼤⼩整除，data_iter函数的⾏为会有什么变化？

答：

如果样本个数不能被批量大小整除，data_iter函数的行为会有所变化。在这种情况下，最后一个批次可能比其他批次要小。

具体来说，假设我们有n个样本和批量大小为b。当n不能被b整除时，最后一个批次将包含不到b个样本。

为了处理这种情况，通常会使用一些特殊的方法，例如填充缺失的样本或者丢弃最后一个不完整的批次。填充缺失的样本可以使用零向量或者其他默认值填充，以使所有批次的大小都相同。丢弃最后一个不完整的批次可以确保每个批次都有相同的大小，但是这样会导致某些样本未被使用。

p106习题

1. 如果将⼩批量的总损失替换为⼩批量损失的平均值，需要如何更改学习率？

答：

根据上面的公式，如果将小批量的总损失替换为小批量损失的平均值，那么学习率通常需要进行相应的调整。具体来说，如果用小批量损失的平均值来更新模型参数，则相当于使用了比原来更小的损失值进行梯度下降优化。因此，为了保持收敛速度不变，可以适当增加学习率。

具体调整学习率的方法因不同的优化算法而异。以基本的随机梯度下降（SGD）算法为例，如果将小批量的总损失替换为小批量损失的平均值，则可以将学习率增加到原来的 batch_size 倍。

例如，如果原来使用的是学习率 lr=0.01 和 batch_size=32，则可以将学习率调整为 lr=0.01*32=0.32。这样做的目的是保持每个迭代步骤中梯度下降的大小不变，从而更好地利用数据集的信息，提高模型的训练效率和性能。

需要注意的是，学习率的调整通常需要根据实际情况进行微调，并综合考虑其他因素如模型复杂度、数据集大小等。

答：