线性反馈移位寄存器LFSR和循环冗余码CRC
线性反馈移位寄存器LFSR和循环冗余码CRC
- 0 前言
- 1 数学基础
-
- 1.1 逻辑异或
- 1.2 模2乘法 和 模2除法
- 2 线性反馈移位寄存器LFSR
-
- 2.1 抽头和特征多项式
- 2.2 3阶线性反馈移位寄存器实例
- 3 循环冗余码CRC
-
- 3.1 CRC的原理
- 3.2 CRC的实例
0 前言
线性反馈移位寄存器(Linear Feedback Shift Register,LFSR)和循环冗余码(Cyclic Redundancy Check,CRC)是微控制器中常用的底层原理。
LFSR用于生成伪随机数,后者用于生成检错码。他们的数学原理都是一样的。
1 数学基础
1.1 逻辑异或
异或运算使用符号⊕或者nor表示,真值表如下
F = A ⊕ B
| A | B | F |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
异或运算可以有3种理解方式:
1 相同得
1,不同得0
2 二进制加法,只留模2的余数,抛弃进位(模2加法)
3 二进制减法,大数减小数,不借位(模2减法)
1.2 模2乘法 和 模2除法
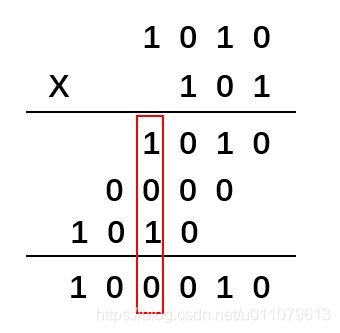
两个二进制数的模2乘法是指在乘法竖式运算中需要做加法的地方都使用异或运算
模2乘法1010 * 101=100010,下图红框中,1⊕0⊕1=0,没有进位
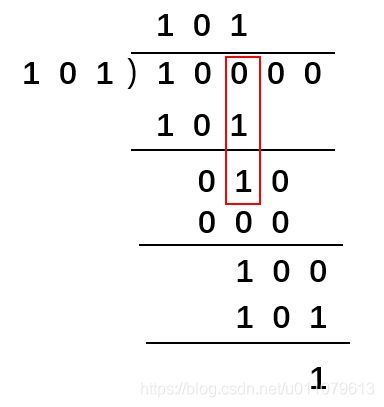
两个二进制数的模2除法是指在除法竖式运算中需要做减法的地方都使用异或运算
模2除法10000 / 101=101余1,下图红框中,0⊕1=1,没有借位
2 线性反馈移位寄存器LFSR
以斐波那契(外部LFSR)为例,有n个二进制寄存器R0-Rn-1,每个寄存器值为0或1
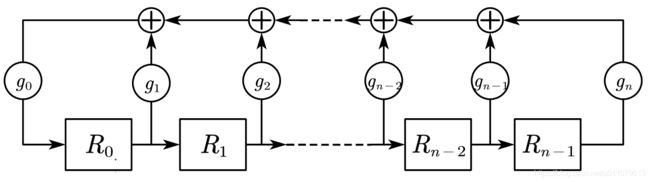
在k阶段,寄存器存在初值,(Rn-1, … R1, R0),称为seed
在k+1阶段,寄存器的值变为:
k+1阶段 |
|---|
| Rn-1 = Rn-2 |
| Rn-2 = Rn-3 |
| … |
| R0 = f(R1, R2, …, Rn-1) = (Rn-1*gn)⊕(Rn-2*gn-1)⊕…⊕(R0*g1)*g0 |
也就是说寄存器存储的结果 (Rn-1, … R1, R0) 每个时钟周期改变一次,其中R1-Rn-1是位移产生,R0是线性反馈函数 f(Rn-1, … R1, R0) 产生,所以称为线性反馈移位寄存器。
线性反馈移位寄存器总是假定g0,gn为1,否则 (Rn-1, … R1, R0) 将在n个周期后恒定为0。
2.1 抽头和特征多项式
f(Rn-1, … R1, R0) = (Rn-1*gn)⊕(Rn-2*gn-1)⊕…⊕(R0*g1)*g0 可以用多项式表示为:
G(x)=gnxn+gn-1xn-1+…+g1x+g0
G(x)称为LFSR的特征多项式
影响线性反馈寄存器下一个状态的 gi = 0 或1叫做抽头,抽头的设定会决定线性反馈寄存器存储的结果 (Rn-1, … R1, R0) 的变化规律。
通常N位的线性反馈寄存器最多有 2N 个不同的状态。但是如果出现初值为N个0的情况,线性反馈寄存器陷入死循环,要排除掉。所以N位线性反馈寄存器能产生最长的不重复序列为 2N-1。
抽头的位置会影响LSFR的最大输出状态的个数
例如:3位的抽头为(g3, g2, g1, g0) = (1, 1, 0, 1)会产生7个状态(多项式对应为:G(x)=x3+x2+1)
若抽头为(g3, g2, g1, g0) = (1, 0, 1, 1),会产生2个状态(多项式对应为:x3+x+1)。
使最大输出序列长度为2N-1的不可约多项式称为LFSR的本原多项式,本原多项式产生的寄存器序列为M序列。
当N位下,本原多项式不是唯一的。下表为不同的位下的本原多项式:
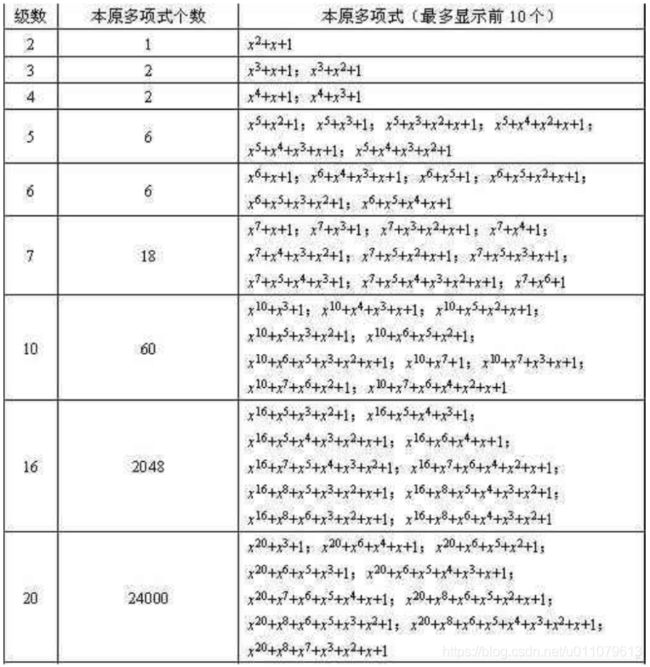

2.2 3阶线性反馈移位寄存器实例
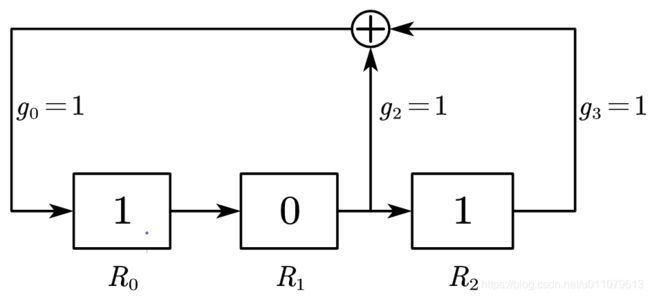
上图为3阶线性反馈移位寄存器
抽头为(g3, g2, g1, g0) = (1, 1, 0, 1)
多项式对应为:G(x)=x3+x2+1
线性反馈函数R0 = f(R2, R1, R0) = R1⊕R2
初始值为SEED = (R2, R1, R0) = (1, 0, 1)
3阶线性反馈移位寄存器周期为7:
| k周期 | (R2, R1, R0) |
|---|---|
| 0 | (1, 0, 1) |
| 1 | (0, 1, 1) |
| 2 | (1, 1, 1) |
| 3 | (1, 1, 0) |
| 4 | (1, 0, 0) |
| 5 | (0, 0, 1) |
| 6 | (0, 1, 0) |
| 7 | (1, 0, 1) |
通过设定seed和抽头,LFSR最多可产生2N-1个序列,这些序列之间看似是随机产生的,之所以称之为伪随机,是因为这些数是通过具体的关系式产生,最终会实现循环。
3 循环冗余码CRC
现实的通信链路都不会是理想的。这就是说,比特在传输的过程中可能会产生差错:1可能会变成0,0可能会变成1,这就叫做比特差错。
因此,为了保证数据传输的可靠性,在计算机网络传输数据时,必须采用各种差错检测措施。
目前在数据链路层广泛使用了循环冗余检测CRC的检测技术
3.1 CRC的原理
CRC运算实际上就是在数据长为k的后面添加供差错检测用的n位冗余码,然后构成帧k+n位发送出去。

选择一个生成多项式,作为对接收的帧进行除法运算时的除数,生成多项式可以写为二进制形式;生成多项式的要求:
①最高位和最低位必须为1;
②当CRC码的任何一位发生错误时,新帧除生成多项式后余数不为0;
③不同位发生错误时,余数应该是不同的;
计算n位冗余码
现假定待传输的数据M = 101001(k = 6),除数p = 1101 (n = 3,p比n多一位)
这n位冗余码可以用下面的方法得出。
(1)用二进制的模2运算进行(2^n)乘M的运算,相当于在M后面添加n个0。
即M后面添加3个0
(2)现在得到M = 101001000(k+n = 9)位的数除以除数p(n = 3)位,
得到余数R =001(n位),R就是冗余码FCS
现在加上CRC后发送的帧是101001001
在接收端把接收到的数据M = 101001001以帧为单位进行CRC检验:把收到的每一个帧都除以相同的除数p(模2运算),然后检查得到的余数R。
如果在传输过程中没有差错,那么经过检验后得到余数R肯定是0。
(读者可以自己检验下,被除数现在是M = 101001001,除数P= 1101,看余数是否为0)
总之,在接收端对接收到的每一个帧经过CRC检验后,有两种情况:
(1)余数R = 0,则判断这个帧没有问题,就接受
(2)余数R != 0,则判断这个帧有差错,就丢弃。
3.2 CRC的实例
假设CRC生成多项式G(X)=X5+X4+X+1,要发送的二进制数据帧为100101110,求CRC校验码:
①把生成多项式转换为二进制数:110011;
②由生成多项式的位数为6可知,CRC校验码的位数为5,所以在数据帧后加5个0,变为10010111000000,将这个数使用模2除法除以生成多项式110011,得到余数即CRC校验码11010;
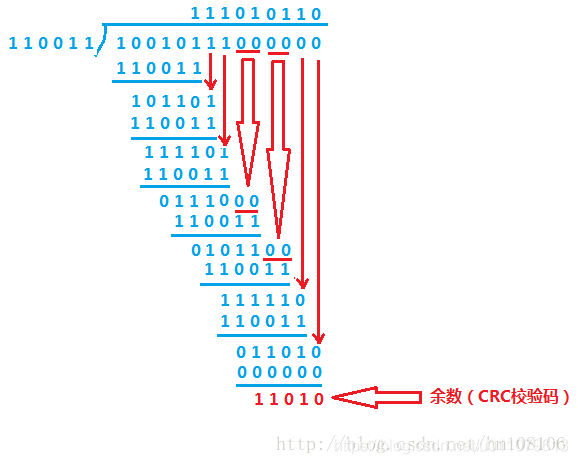
③用得到的CRC校验码替换掉数据帧中的5个0,形成新的帧10010111011010,将这个新帧发送给接收端;
④接收端收到新帧后,用新帧除以上面的多项式110011(模2除法),如果余数为0,该数据帧在传输过程中没有出错,否则出错;(经验证余数为0)