机器学习之基于BP神经网络的预测

BP神经网络具有以下优点：

1) 非线性映射能力：BP神经网络实质上实现了一个从输入到输出的映射功能，数学理论证明三层的神经网络就能够以任意精度逼近任何非线性连续函数。这使得其特别适合于求解内部机制复杂的问题，即BP神经网络具有较强的非线性映射能力。

2) 自学习和自适应能力：BP神经网络在训练时，能够通过学习自动提取输入、输出数据间的“合理规则”，并自适应地将学习内容记忆于网络的权值中。即BP神经网络具有高度自学习和自适应的能力。

3) 泛化能力：所谓泛化能力是指在设计模式分类器时，即要考虑网络在保证对所需分类对象进行正确分类，还要关心网络在经过训练后，能否对未见过的模式或有噪声污染的模式，进行正确的分类。也即BP神经网络具有将学习成果应用于新知识的能力。

BP神经网络具有以下缺点：

1) 局部极小化问题：从数学角度看，传统的 BP神经网络为一种局部搜索的优化方法，它要解决的是一个复杂非线性化问题，网络的权值是通过沿局部改善的方向逐渐进行调整的，这样会使算法陷入局部极值，权值收敛到局部极小点，从而导致网络训练失败。加上BP神经网络对初始网络权重非常敏感，以不同的权重初始化网络，其往往会收敛于不同的局部极小，这也是每次训练得到不同结果的根本原因。

2) BP 神经网络算法的收敛速度慢：由于BP神经网络算法本质上为梯度下降法，它所要优化的目标函数是非常复杂的，因此，必然会出现“锯齿形现象”，这使得BP算法低效；又由于优化的目标函数很复杂，它必然会在神经元输出接近0或1的情况下，出现一些平坦区，在这些区域内，权值误差改变很小，使训练过程几乎停顿；BP神经网络模型中，为了使网络执行BP算法，不能使用传统的一维搜索法求每次迭代的步长，而必须把步长的更新规则预先赋予网络，这种方法也会引起算法低效。以上种种，导致了BP神经网络算法收敛速度慢的现象。

3) BP 神经网络结构选择不一：BP神经网络结构的选择至今尚无一种统一而完整的理论指导，一般只能由经验选定。网络结构选择过大，训练中效率不高，可能出现过拟合现象，造成网络性能低，容错性下降，若选择过小，则又会造成网络可能不收敛。而网络的结构直接影响网络的逼近能力及推广性质。因此，应用中如何选择合适的网络结构是一个重要的问题。

实现乳腺癌分类

1.首先是库函数的导入

# 导入乳腺癌数据集
from sklearn.datasets import load_breast_cancer
# 导入BP模型
from sklearn.neural_network import MLPClassifier
# 导入训练集分割方法
from sklearn.model_selection import train_test_split 
# 导入预测指标计算函数和混淆矩阵计算函数
from sklearn.metrics import classification_report, confusion_matrix
# 导入三维显示工具
from mpl_toolkits.mplot3d import Axes3D
# 导入绘图包
import seaborn as sns
import matplotlib.pyplot as plt

其中，classification_report 和 confusion_matrix 函数分别用于生成分类报告和混淆矩阵。 分类报告是一个格式化的文件，其中包含了分类器在给定数据集上的性能指标，例如精确度、召回率、F1 值等。可以使用 classification_report 函数将分类器的性能指标输出为分类报告文件。 混淆矩阵是一个二维矩阵，其中行表示实际标签，列表示预测标签。可以使用 confusion_matrix 函数将分类器在给定数据集上的混淆矩阵输出为混淆矩阵文件。

2.导入乳腺癌数据集

cancer = load_breast_cancer()

我们来打印看一下数据格式，通过数据我们发现它有30个数据类型，每个类型有569条数据。此外还有一个标签列，1代表患有乳腺癌，0代表不患病。

 为了更好的处理数据，将数据集转换为datafrme格式，feature是特征，target是标签

feature = cancer.data
target = cancer.target
feature = pd.DataFrame(feature,columns=cancer.feature_names)
target = pd.DataFrame(target,columns=['target'])

 3.划分训练集和测试集

train_test_split函数的作用是将数据集划分为两个部分：训练集和测试集。训练集用于模型的训练，测试集用于模型的测试。通过这种方式，可以减少在测试集上进行的无效计算，并且可以在训练集上进行更多的模型训练，以提高模型的准确性和泛化能力。test_size=0.2表示测试集占总数据集的20%，random_state表示随机森林当指定一个数时则每次划分的结果都相同。

x_train,x_test,y_train,y_test = train_test_split(feature,target['target'],test_size=0.2,random_state=42) 

 4.建立PB模型

定义模型参数

solver = 'adam' # 优化算法
activation = 'relu' # 激活函数
max_iter = 500 # 最大迭代次数
alpha = 1e-3 # 学习率衰减系数
hidden_layer_sizes = (32,32) # 隐藏层大小
random_state = 1 # 随机种子
alpha = 1e-3 的意思是在控制神经网络的训练过程中，设置学习率衰减的速率。具体来说，它指的是学习率从 0.01 慢慢衰减到 0.001 的过程中，每次衰减的步长为 0.01。 通常来说，将 alpha 的值设置在 0.01 到 0.1 之间比较合适。

# 建立 BP 模型, 采用Adam优化器，relu非线性映射函数
BP = MLPClassifier(solver='adam',activation = 'relu',max_iter = 1000,alpha = 1e-3,hidden_layer_sizes = (64,32, 32),random_state = 1)
# 进行模型训练
BP.fit(x_train, y_train)

5.模型预测及可视化

Axes3D是Matplotlib的一个扩展模块，提供了三维坐标系的功能，可以用于绘制三维图形和图表。它通过在二维坐标系中添加一个额外的维度来实现这一目标，使得在绘制三维图形时可以更加直观和方便。

其中，rect 的值为 [0, 0, 1, 1]，表示 x 轴范围为 0 到 1，y 轴范围为 0 到 1，z 轴范围为 0 到 1。 elev 参数指定了 3D 坐标系中的视野高度，elev 的值为 20，表示观察者距离 3D 坐标系中心点的距离为 20。 azim 参数指定了 3D 坐标系中的视野方向，azim 的值为 20，表示 z 轴的范围为 -20 到 20。

这里随机选用三组数据做演示，可根据实际情况更改。

# 进行模型预测
predict_train_labels = BP.predict(x_test)
# 可视化真实数据
fig = plt.figure(figsize=(5,5))
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=20, azim=20) 
fig.add_axes(ax)
ax.scatter(x_test['mean radius'], x_test['mean texture'], x_test['mean perimeter'], marker='o', c=y_test)
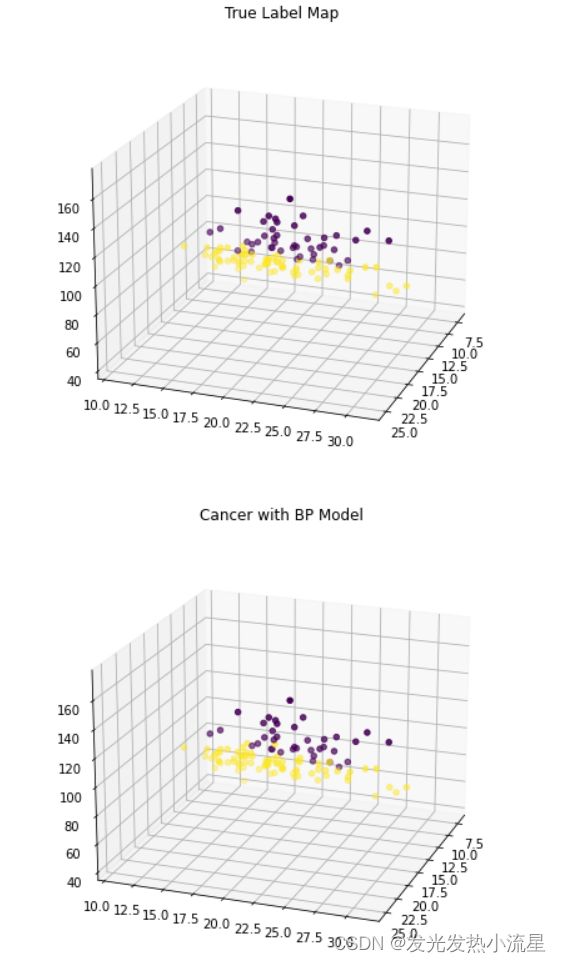
plt.title('True Label Map')
plt.show()
# 可视化预测数据
fig = plt.figure(figsize=(5.,5))
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=20, azim=20) 
fig.add_axes(ax)
ax.scatter(x_test['mean radius'], x_test['mean texture'], x_test['mean perimeter'], marker='o', c=predict_train_labels)
plt.title('Cancer with BP Model')
plt.show()

结果如下：一个是真实值，另一个是预测值。

 我们来看一下这个模型的预测准确率如何

 准确率到达94%，效果还不错。

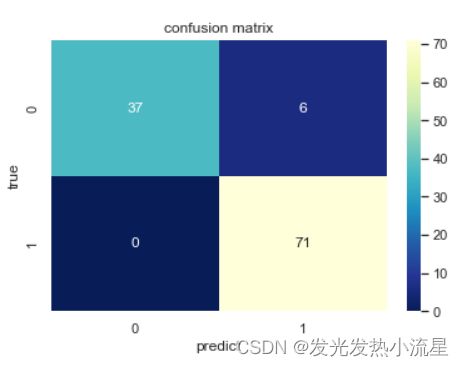
 再来看一下混淆矩阵吧。

6.重要知识点

BP神经网络模型要点在于数据的前向传播和误差反向传播，来对参数进行更新，使得损失最小化。 误差反向传播算法简称反向传播算法（即BP算法）。使用反向传播算法的多层感知器又称为BP神经网络。BP算法是一个迭代算法，它的基本思想为：
（1）先计算每一层的状态和激活值，直到最后一层（即信号是前向传播的）；
（2）计算每一层的误差，误差的计算过程是从最后一层向前推进的（这就是反向传播算法名字的由来）；
（3）更新参数（目标是误差变小）。迭代前面两个步骤，直到满足停止准则（比如相邻两次迭代的误差的差别很小）。
在这个过程，函数的导数链式法则求导很重要，需要手动推导BP神经网络模型的梯度反向传播过程，熟练掌握链式法则进行求导，对参数进行更新。

还不知道如何绘制热力图可以看看这篇文章：

http://t.csdn.cn/c5CYE