【剑指offer刷题记录 java版】数组双指针 之 二分搜索
本系列文章记录labuladong的算法小抄中剑指offer题目
【剑指offer刷题记录 java版】数组双指针 之 二分搜索
- 剑指 Offer 53 - I. 在排序数组中查找数字 I
- 剑指 Offer II 068. 查找插入位置
- 剑指 Offer 04. 二维数组中的查找
- 剑指 Offer II 069. 山峰数组的顶部
- 剑指 Offer II 073. 狒狒吃香蕉(难)
- 剑指 Offer 53 - II. 0~n-1中缺失的数字
- 总结
剑指 Offer 53 - I. 在排序数组中查找数字 I
题目链接:https://leetcode.cn/problems/zai-pai-xu-shu-zu-zhong-cha-zhao-shu-zi-lcof/

class Solution {
public int search(int[] nums, int target) {
int mid = erfen(nums,target);
//未找到等于target的下标,返回0
if(mid==-1)return 0;
//向两边寻找边界并计数
int left=mid,right=mid;
int count=1;
while(--left>=0 && nums[left]==target)count++;
while(++right<nums.length && nums[right]==target)count++;
return count;
}
//二分搜索
public int erfen(int[] nums, int target){
int left=0,right=nums.length-1;//左闭右闭
int mid;
while(left<=right){
mid = (left+right)/2;
if(nums[mid]<target){
left=mid+1;
}else if(nums[mid]>target){
right=mid-1;
}else{
return mid;
}
}
return -1;
}
}
剑指 Offer II 068. 查找插入位置
题目链接:https://leetcode.cn/problems/N6YdxV/description/


class Solution {
public int searchInsert(int[] nums, int target) {
//因为1 <= nums.length <= 10^4,不需要判空
// if(nums.length==0)return 0;
int left=0, right=nums.length-1;//左闭右闭
int mid=0;
while(left<=right){
mid=(left+right)/2;
if(nums[mid]<target){
left=mid+1;
}else if(nums[mid]>target){
right=mid-1;
}else{
return mid;
}
}
return left;
}
}
剑指 Offer 04. 二维数组中的查找
题目链接:https://leetcode.cn/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/

class Solution {
public boolean findNumberIn2DArray(int[][] matrix, int target) {
//从右上角或者左下角出发,保证两个方向一个增大一个减小
// 这样避免了采用动态规划的穷举
int m=matrix.length-1,n=0;//从左下角出发
while(m>=0 && n<matrix[0].length){
if(matrix[m][n]>target){
m--;
}else if(matrix[m][n]<target){
n++;
}else{
return true;
}
}
return false;
}
}
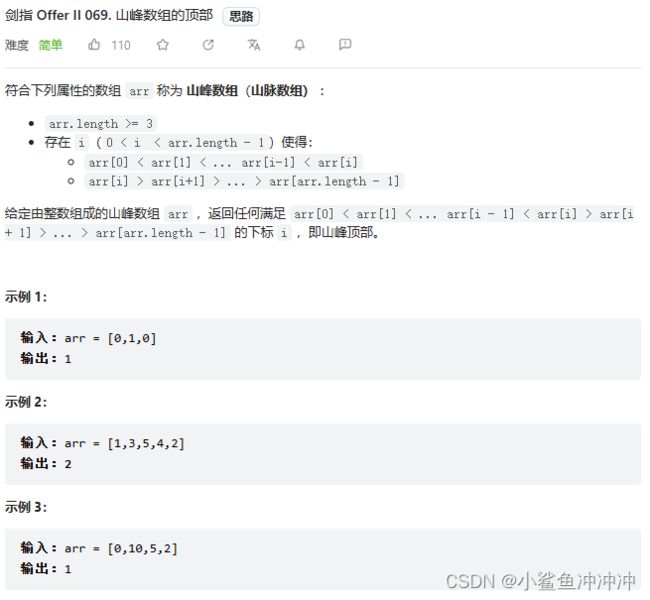
剑指 Offer II 069. 山峰数组的顶部
题目链接:https://leetcode.cn/problems/B1IidL/

class Solution {
public int peakIndexInMountainArray(int[] arr) {
int left=0,right=arr.length-1;//左闭右闭
// 因为题目必然有解,所以设置 left == right 为结束条件
while(left<right){
int mid = (right+left)/2;
if(arr[mid]<arr[mid+1]){
// mid+1 本身就是峰值或其右侧有一个峰值
left=mid+1;
}else{
right=mid;
}
}
return left;
}
}
剑指 Offer II 073. 狒狒吃香蕉(难)
题目链接:https://leetcode.cn/problems/nZZqjQ/

class Solution {
public int minEatingSpeed(int[] piles, int h) {
/**
本题的非严格单调数组没有显示表示,需要自己定义
可以发现,肥狒狒能吃掉全部香蕉的时间 getTime(k) 随着 吃香蕉速度k 增大而增大
因此可以将吃香蕉速度看作下标,吃掉全部香蕉的时间为数组元素
本题转换为寻找数组中小于等于给定时间h的最大下标
*/
int left=1,right=1000000000;//左闭右闭
while(left<=right){
int mid = (left+right)/2;
if(getTime(mid,piles)>h){
left=mid+1;
}else if(getTime(mid, piles)<=h){
right=mid-1;
}
}
return left;
}
// 定义:速度为 k 时,需要 getTime(k) 小时吃完所有香蕉
public int getTime(int k, int[] piles){
int time=0;
for(int i=0;i<piles.length;i++){
time += piles[i] / k;
if (piles[i] % k > 0) {
time++;
}
}
return time;
}
}
剑指 Offer 53 - II. 0~n-1中缺失的数字
题目链接:https://leetcode.cn/problems/que-shi-de-shu-zi-lcof/

class Solution {
public int missingNumber(int[] nums) {
int left=0,right=nums.length-1;
int mid=0;
while(left<=right){
mid=(left+right)/2;
if(nums[mid]>mid){
right=mid-1;
}else if(nums[mid]==mid){
left=mid+1;
}
}
return left;//这里巧妙地使用下标替换数组值,避免了下标超范围的问题
}
}
总结
二分查找建立在有序的和基础上,复杂度是O( log(n) )。