C++【二叉树进阶试题】
✨个人主页: 北 海
所属专栏: C/C++相关题解
操作环境: Visual Studio 2019 版本 16.11.17
![]()
文章目录
- 606. 根据二叉树创建字符串
- 102. 二叉树的层序遍历
- 107. 二叉树的层序遍历 II
- 236. 二叉树的最近公共祖先
- JZ36 二叉搜索树与双向链表
- 105. 从前序与中序遍历序列构造二叉树
- 106. 从中序与后序遍历序列构造二叉树
- 144. 二叉树的前序遍历
- 94. 二叉树的中序遍历
- 145. 二叉树的后序遍历
这是一篇关于 二叉树 题解博客,主要包含以下题目,可根据当前文章中的目录随意跳转查看
606. 根据二叉树创建字符串
题目链接:606. 根据二叉树创建字符串
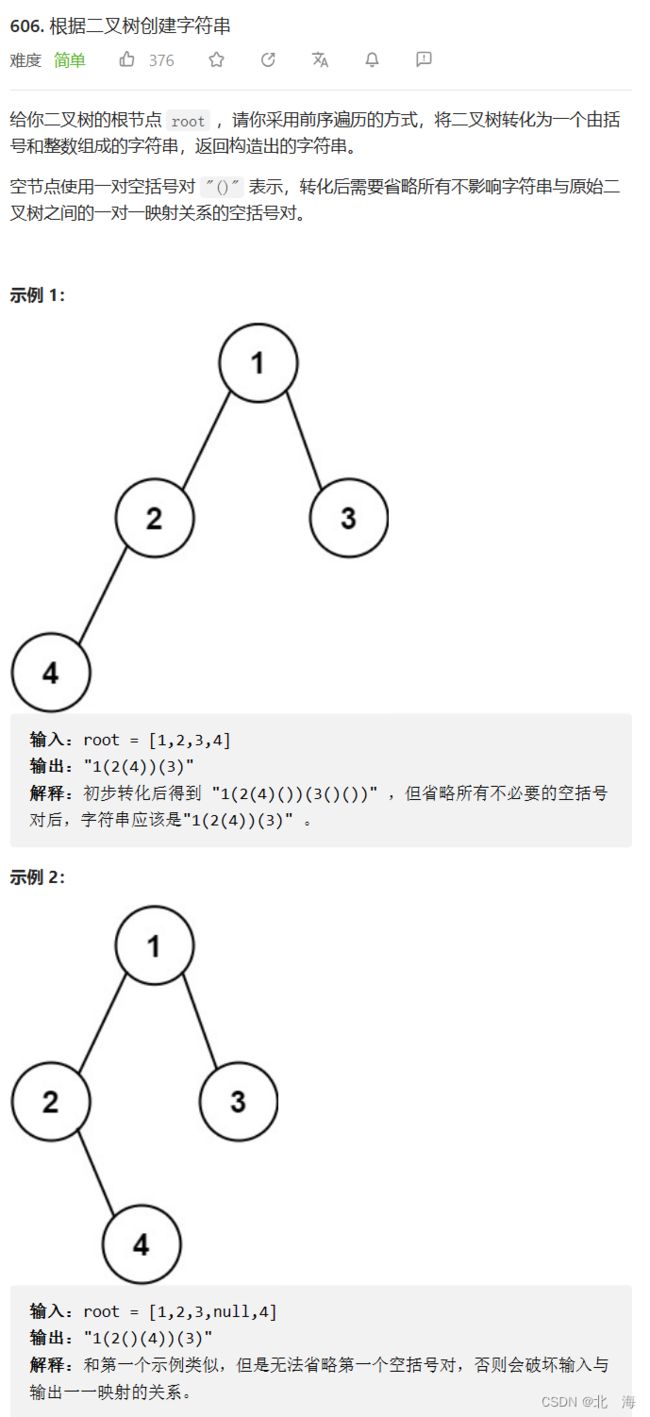
题目分析:对二叉树进行前序遍历,并将遍历的结果转化为字符串,同时需要对 左右子树 加上 () 修饰,必要的 () 不能省略,比如:左子树不存在,但右子树存在,那么左子树的 () 就不能省略
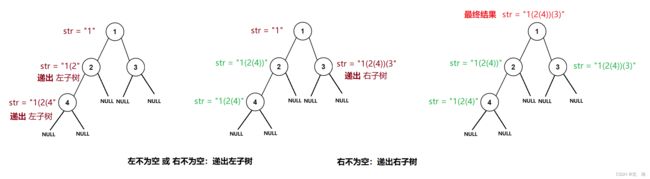
解题思路:首选递归解决,大问题化小问题,首先将 根节点转化为字符串,然后判断 [左子树 || 右子树] 是否存在,如果存在,则递归左子树,再判断 [右子树] 是否存在,如果存在,则递归右子树
//606. 根据二叉树创建字符串
//https://leetcode.cn/problems/construct-string-from-binary-tree/
class Solution {
public:
void _tree2str(TreeNode* root, string& str)
{
if(root == nullptr)
return;
str += to_string(root->val); //先将根的值并入字符串中
//判断是否需要递归子树
if(root->left != nullptr || root->right != nullptr)
{
//左右其中一个不为空,都需要递归左子树
str += "(";
_tree2str(root->left, str);
str += ")";
}
if(root->right != nullptr)
{
//右不为空,才递归右子树
str += "(";
_tree2str(root->right, str);
str += ")";
}
}
string tree2str(TreeNode* root) {
string str; //创建后的字符串
_tree2str(root, str); //建议再封装一层,方便递归
return str;
}
};
注意: 因为是递归,所以参数2 str 需要使用引用,确保在不同栈帧中对同一个字符串进行操作
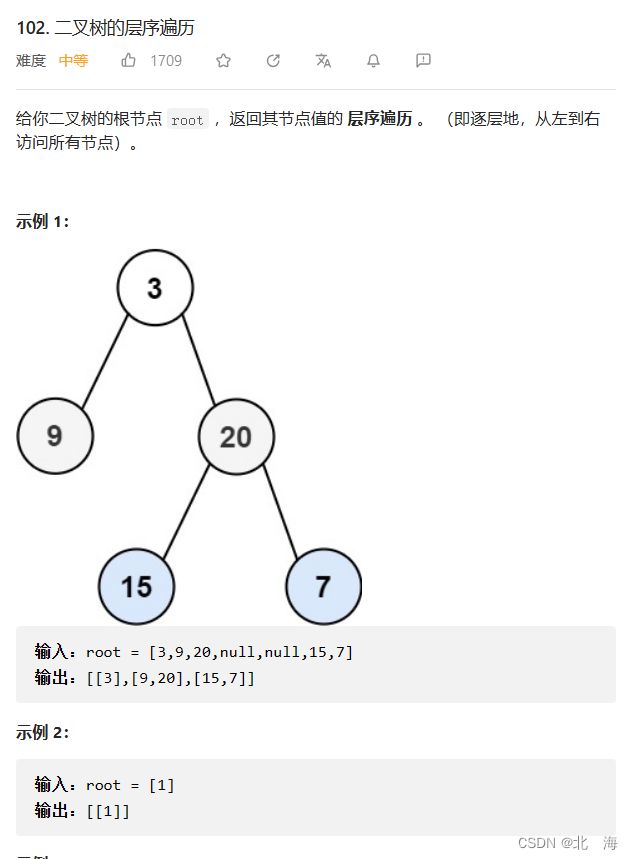
102. 二叉树的层序遍历
题目链接:102. 二叉树的层序遍历
题目分析:层序遍历的升级版,层序遍历后,要求将每一层的结果作为一个一维数组,存入二维数组中
解题思路:在层序遍历思想的基础上,将每一层的节点数统计起来,出结果时,以节点数为主
层序遍历思想:借助队列,首先根节点入队,然后出队,并将存在的左右子节点带入队中,重复此过程,直到队列为空
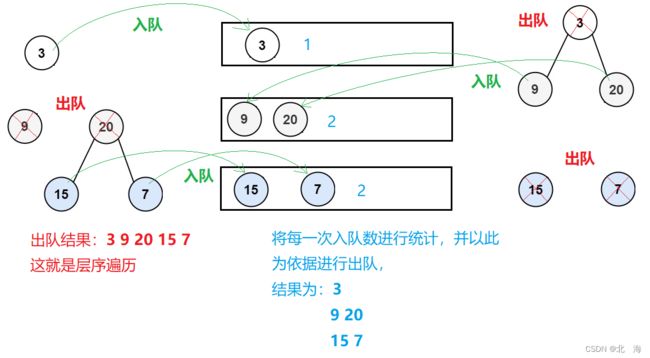
所以本题的解题关键就在于 入队时要额外使用一个计数器统计当前队列中的节点数,方面后面出队
//102. 二叉树的层序遍历
//https://leetcode.cn/problems/binary-tree-level-order-traversal/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> vv; //二维数组
if(root == nullptr)
return vv;
queue<TreeNode*> q; //存储节点的队列
q.push(root);
int cnt = q.size(); //当前队列中的节点数
//层序遍历思想
while(!q.empty())
{
vector<int> v; //这一次的遍历结果
//根据节点数进行出队
while(cnt--)
{
TreeNode* cur = q.front();
q.pop();
v.push_back(cur->val);
if(cur->left != nullptr)
q.push(cur->left);
if(cur->right != nullptr)
q.push(cur->right);
}
//这一层的结果入二维数组
vv.push_back(v);
//重新更新节点数
cnt = q.size();
}
return vv;
}
};
注意: 在单层遍历结束后,需要更新计数器的值
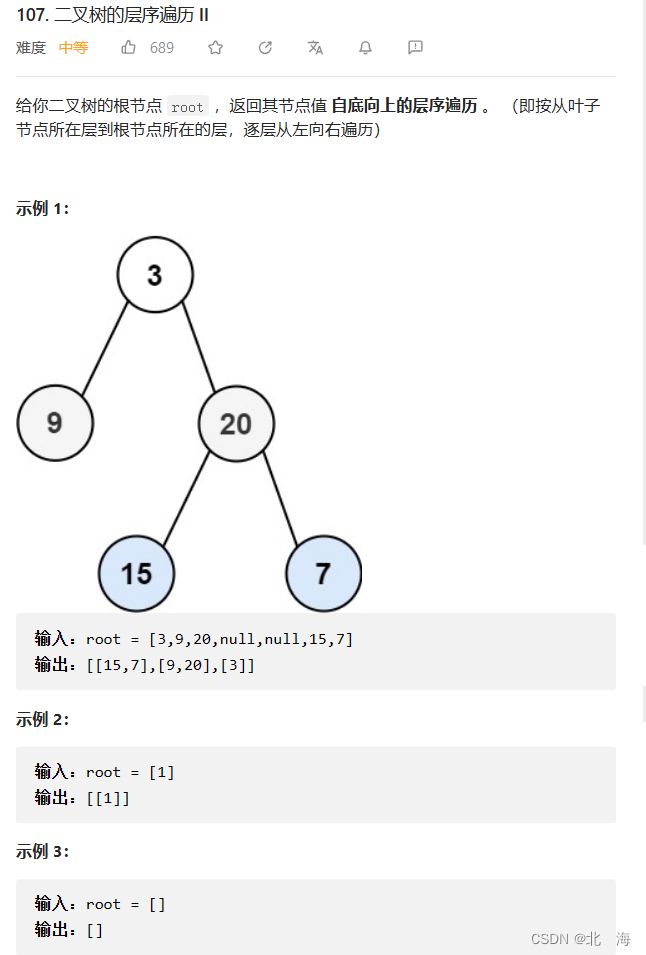
107. 二叉树的层序遍历 II
题目链接:107. 二叉树的层序遍历 II
题目分析:在上一题的基础上,把结果进行逆置即可
//107. 二叉树的层序遍历 II
//https://leetcode.cn/problems/binary-tree-level-order-traversal-ii/
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> vv; //二维数组
if(root == nullptr)
return vv;
queue<TreeNode*> q; //存储节点的队列
q.push(root);
int cnt = q.size(); //当前队列中的节点数
//层序遍历思想
while(!q.empty())
{
vector<int> v; //这一次的遍历结果
//根据节点数进行出队
while(cnt--)
{
TreeNode* cur = q.front();
q.pop();
v.push_back(cur->val);
if(cur->left != nullptr)
q.push(cur->left);
if(cur->right != nullptr)
q.push(cur->right);
}
//这一层的结果入二维数组
vv.push_back(v);
//重新更新节点数
cnt = q.size();
}
//重要的一步:逆置
reverse(vv.begin(), vv.end());
return vv;
}
};
236. 二叉树的最近公共祖先
题目链接:236. 二叉树的最近公共祖先

题目分析:二叉树中的经典题目,某个节点到根节点的路径是唯一的,路径中的节点都是其祖先,如果某两个节点的路径出出现了交叉,那么这个交叉点就是他们公共的祖先。值得注意的是,节点也是自己的祖先,所以节点 p 可以成为 节点 p 与 节点 q 的公共祖先,同理,节点 q 也行
这里提供两种解题思路,前者比较容易想到,后者则比较巧妙
解题思路1:某个节点的左右子树中如果分别包含 p、q 节点,那么这个节点就是它们的祖先节点,将问题转化为判断节点是否存在于子树中
//236. 二叉树的最近公共祖先
//https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/
class Solution {
public:
bool findVal(TreeNode* root, TreeNode* node)
{
if(root == nullptr)
return false;
return root == node ||
findVal(root->left, node) ||
findVal(root->right, node);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == nullptr)
return nullptr;
//如果当前节点为其中一个目标节点,则为最近公共祖先
if(root == p || root == q)
return root;
//分别到左右子树中找 p、q
bool leftP = findVal(root->left, p);
bool rightP = findVal(root->right, p);
bool leftQ = findVal(root->left, q);
bool rightQ = findVal(root->right, q);
//只要其中一组合法,当前节点就是公共祖先,否则递归向下找
if((leftP && rightQ) || (leftQ && rightP))
return root;
//都在左子树,去左子树找
else if(leftP && leftQ)
return lowestCommonAncestor(root->left, p, q);
//都在右子树,去右子树找
else
return lowestCommonAncestor(root->right, p, q);
}
};
这种解法的优点就是 容易想到,书写简单,缺点就很明显了 慢,非常慢,最坏的情况下每一个节点都需要进行一遍查找
所以就有了解法2
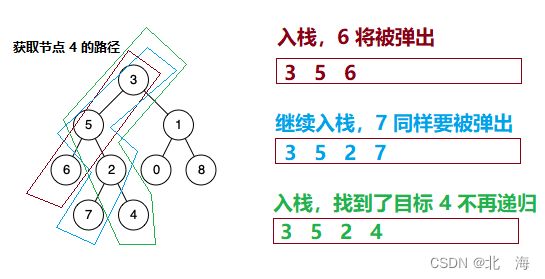
解题思路2:既然每个节点到根的路径是唯一的,那么可以把路径记录下来,然后将问题转换为链表相交问题
如何获取路径:后序遍历思想,将节点保存入栈中,不包含在目标值路径中的需要弹出
//236. 二叉树的最近公共祖先
//https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/
//解法2:获取路径
class Solution {
public:
bool getPath(TreeNode* root, const TreeNode* node, stack<TreeNode*>& path)
{
if(root == nullptr)
return false;
//先将节点入栈
path.push(root);
if(root == node)
return true;
//判断左右子路径中包含 node 节点
bool inLeft = getPath(root->left, node, path);
bool inRight = getPath(root->right, node, path);
if(inLeft == false && inRight == false)
{
//此节点的子树中必然不包含 node 节点
//无用,需要弹出
path.pop();
return false;
}
return true;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack<TreeNode*> pPath; //路径
stack<TreeNode*> qPath;
//获取路径
getPath(root, p, pPath);
getPath(root, q, qPath);
//长的路径先走
while(pPath.size() != qPath.size())
{
if(pPath.size() > qPath.size())
pPath.pop();
else
qPath.pop();
}
//一起弹出,寻找最近公共祖先
while(pPath.size())
{
if(pPath.top() == qPath.top())
break;
pPath.pop();
qPath.pop();
}
return pPath.top();
}
};
这种解法的优势就很明显了 速度极快
注意:
getPath函数的返回值仅仅是用来评判当前节点是否会被弹出- 参数3
stack需要使用引用,确保在不同栈帧中修改的是同一个路径
JZ36 二叉搜索树与双向链表
题目链接:JZ36 二叉搜索树与双向链表

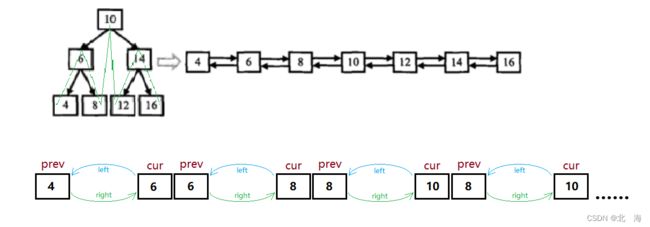
题目分析:将二叉树变成双向链表,因为二叉每个节点都有左、右指针,就像双向链表中的前、后指针一样,所以可以将其进行转换;其实这里是一棵二叉搜索树,而题目要求转换后的双向链表有序,可以借助二叉搜索树的特性:中序遍历有序来进行转换
解题思路:在二叉树中序遍历的基础之上,传递指向当前节点的指针和指向上一个节点的指针,在两者之间建立链接关系,当中序遍历结束后,双向链表就转换完成了
为什么是
prev的right链接cur?
- 因为当前是中序遍历(左根右),
prev是上一个节点,left已链接了上上一个节点,不能更改
//JZ36 二叉搜索树与双向链表
//https://www.nowcoder.com/practice/947f6eb80d944a84850b0538bf0ec3a5?tpId=13&&tqId=11179&rp=1&ru=/activity/oj&qru=/ta/coding-interviews/question-ranking
class Solution {
public:
void treeTransToList(TreeNode* cur, TreeNode*& prev) {
if (cur == nullptr)
return;
treeTransToList(cur->left, prev);
if (prev != nullptr) {
//细节: prev 的 right 链接 cur
// cur 的 left 链接 prev
prev->right = cur;
cur->left = prev;
}
prev = cur;
treeTransToList(cur->right, prev);
}
TreeNode* Convert(TreeNode* pRootOfTree) {
//记录上一次遍历的节点,与之建立链接关系
TreeNode* prev = nullptr;
treeTransToList(pRootOfTree, prev);
//找到最左节点,即头节点
TreeNode* head = pRootOfTree;
while (head != nullptr && head->left != nullptr)
head = head->left;
return head;
}
};
注意:
- 传递参数时,上一个节点需要使用引用接收,链接不同栈帧中的节点
- 寻找最左节点时,需要先对当前节点做判空处理,避免野指针
105. 从前序与中序遍历序列构造二叉树
题目链接:105. 从前序与中序遍历序列构造二叉树
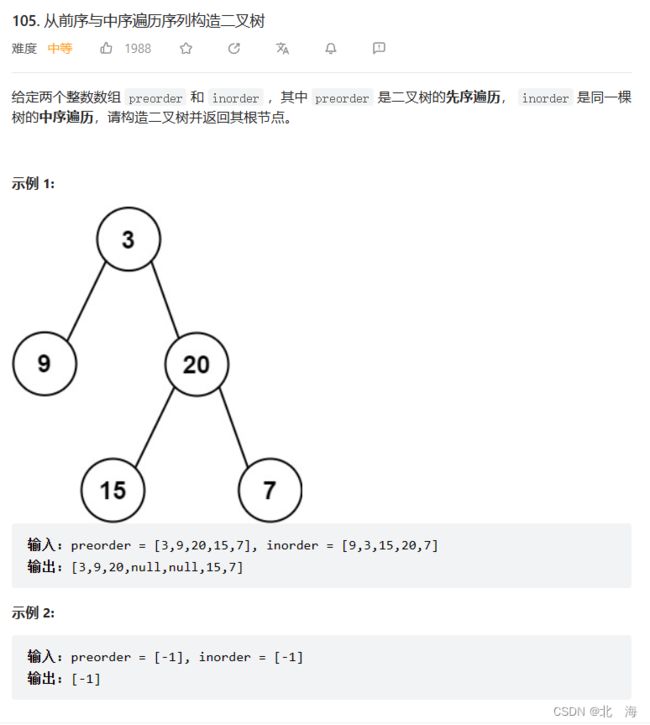
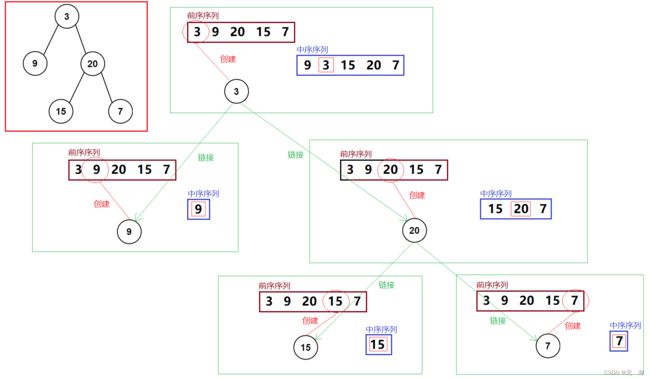
题目分析:给定一个前序和中序遍历,还原出二叉树,前序【根左右】、中序【左根右】,因此前序序列中的第一个节点一定是整个二叉树的根
解题思路:传递前序和中序序列,根据前序序列中的节点,创建根节点,再去中序序列中找到找到左右子树区间,创建左右子树,进行链接
//105. 从前序与中序遍历序列构造二叉树
//https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
class Solution {
public:
TreeNode* _buildTree(vector<int>& preorder, int& pos, vector<int>& inorder, int begin, int end)
{
//如果区间非法,就返回空
if(begin >= end)
return nullptr;
//创建当前节点
TreeNode* root = new TreeNode(preorder[pos]);
int rooti = begin;
//从中序序列中划分出区间 [begin, rooti) [rooti + 1, end)
while(rooti < end)
{
if(preorder[pos] == inorder[rooti])
break;
rooti++;
}
pos++; //重要,每构建一个节点,前序序列节点 -1
//链接左右子树
root->left = _buildTree(preorder, pos, inorder, begin, rooti);
root->right = _buildTree(preorder, pos, inorder, rooti + 1, end);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
//前序确认根
//中序确认子树
int pos = 0;
TreeNode* root = _buildTree(preorder, pos, inorder, 0, inorder.size());
return root;
}
};
注意: 前序序列的下标 pos 需要使用引用,因为每个栈帧中的节点创建都会使 pos 发生改变,即不同栈帧中的 pos 是同一个
106. 从中序与后序遍历序列构造二叉树
题目链接:106. 从中序与后序遍历序列构造二叉树
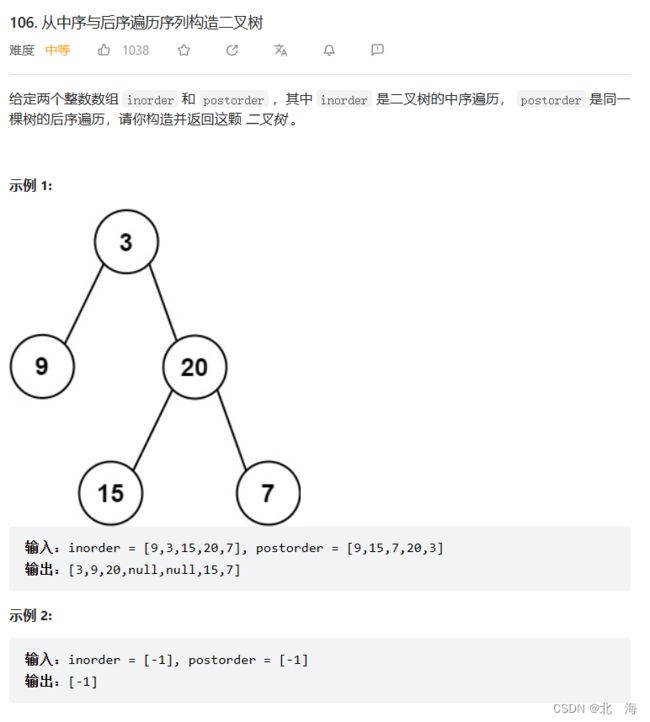
题目分析:前序、中序可以重构二叉树,中序、后序同样也可以,因为后序一样可以确认根,然后一样从中序序列中划分区间
解题思路:反向遍历后序序列,创建根节点,从中序序列中划分出左右区间,递归获取结果后进行链接
//106. 从中序与后序遍历序列构造二叉树
//https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/
class Solution {
public:
TreeNode* _buildTree(vector<int>& inorder, int begin, int end, vector<int>& postorder, int& pos)
{
if(begin >= end)
return nullptr;
TreeNode* root = new TreeNode(postorder[pos]);
int rooti = begin;
//根据根节点的值,划分子区间 [begin, rooti) [rooti + 1, end)
while(rooti < end)
{
if(inorder[rooti] == postorder[pos])
break;
rooti++;
}
pos--; //注意:后序 pos 是--
//注意:后序需要先链接右子树,再链接左子树
root->right = _buildTree(inorder, rooti + 1, end, postorder, pos);
root->left = _buildTree(inorder, begin, rooti, postorder, pos);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
//后序确定根
//中序确定子树
int pos = postorder.size() - 1;
TreeNode* root = _buildTree(inorder, 0, inorder.size(), postorder, pos);
return root;
}
};
注意: 中序、后序重构二叉树时,需要先链接右子树,再链接左子树
144. 二叉树的前序遍历
题目链接:144. 二叉树的前序遍历
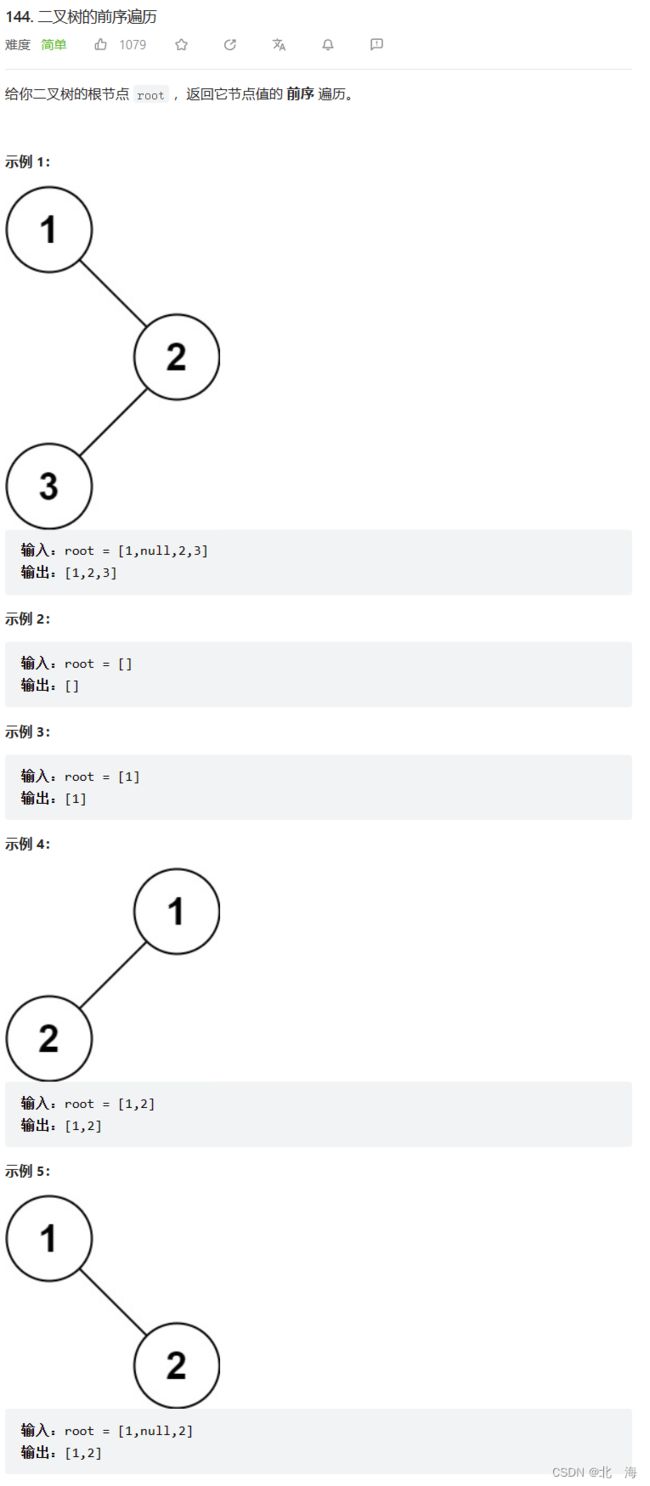
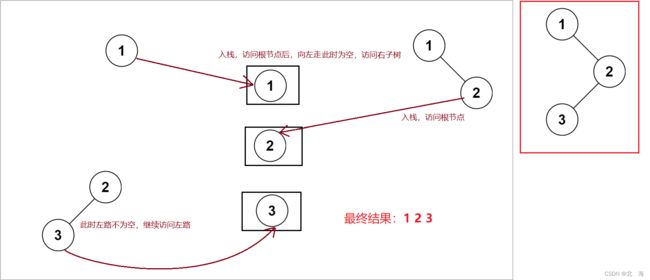
题目分析:前序遍历【根左右】,二叉树的必备技能,递归写法很简单,几行代码就解决了,因此这里挑战的是迭代写法
解题思路:利用栈模拟递归过程,先访问根节点,然后向左走,直到走到空,访问完左路节点后,判断右子树是否为空,不为空则往右走
//144. 二叉树的前序遍历
//https://leetcode.cn/problems/binary-tree-preorder-traversal/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
//前序:根左右
//借助栈模拟递归过程
stack<TreeNode*> node;
vector<int> v;
TreeNode* cur = root;
while(cur || !node.empty())
{
//先访问根节点及左路节点
while(cur)
{
node.push(cur);
v.push_back(cur->val);
cur = cur->left; //访问左路节点
}
TreeNode* top = node.top();
node.pop();
if(top->right != nullptr)
cur = top->right;
}
return v;
}
};
注意: 如果右路为空,是不需要更新 cur 的,即不需要访问右路节点
94. 二叉树的中序遍历
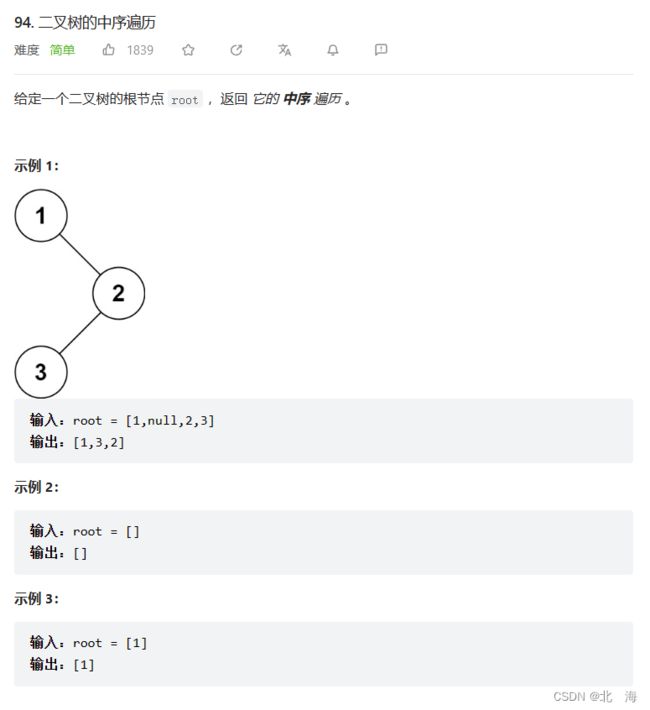
题目链接:94. 二叉树的中序遍历
解题思路:跟前序遍历一样,利用栈模拟递归过程,先向左走,将结果入栈,直到走到空,然后访问栈顶元素(根),再判断是否需要访问右路节点
//94. 二叉树的中序遍历
//https://leetcode.cn/problems/binary-tree-inorder-traversal/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
//中序:左根右
stack<TreeNode*> node;
vector<int> v;
TreeNode* cur = root;
while(cur || !node.empty())
{
//先将左路节点入栈
while(cur)
{
node.push(cur);
cur = cur->left;
}
//访问根节点
TreeNode* top = node.top();
node.pop();
v.push_back(top->val);
//判断是否需要访问右路节点
if(top->right != nullptr)
cur = top->right;
}
return v;
}
};
145. 二叉树的后序遍历
题目链接:145. 二叉树的后序遍历
题目分析:后序遍历【左右根】,通过迭代实现,不过后序会更难一些
解题思路:一样用栈模拟递归过程,先访问左路节点,然后判断是否能访问根节点:右路为空 或者 右节点已经访问过,才能访问根节点,否则只能先访问右路节点
//145. 二叉树的后序遍历
//https://leetcode.cn/problems/binary-tree-postorder-traversal/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
//后序:左右根
stack<TreeNode*> node;
vector<int> v;
TreeNode* prev = nullptr;
TreeNode* cur = root;
while(cur || !node.empty())
{
//先访问左路节点
while(cur)
{
node.push(cur);
cur = cur->left;
}
TreeNode* top = node.top();
//判断是否需要访问根
//条件:右为空 或者 右节点已经访问过了
if(top->right == nullptr || (top->right == prev))
{
v.push_back(top->val);
node.pop();
prev = top;
}
//访问右路节点
else
cur = top->right;
}
return v;
}
};
![]()
相关文章推荐
Day6 不要二、把字符串转换成整数
Day5 统计回文、连续最大和
Day4 计算糖果、进制转换
Day3 字符串中找出连续最长的数字串、数组中出现次数超过一半的数字
Day2 排序子序列、倒置字符串
Day1 组队竞赛、删除公共字符