Geometric Shapes (poj3449多边形相交)
题意:给你一些多边形的点,判断每个多边形和那些多边形相交,编号按照字典序输出
思路:枚举每个多边形的每条边看是否相交,这里的相交是包括端点的,关键是给你正方形不相邻两个点求另外两个点怎么求,长方形给你3个点求第四个点怎么求?
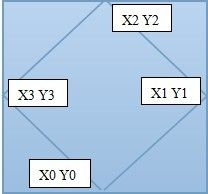
因为对角线的交点为两条对角线的中点,所以
x0 + x2 = x1 + x3
y0 + y2 = y1 + y3
可以证明分割的这几个小三角形是全等的所以有
x1 - x3 = y2 - y1
y1 - y3 = x2 - x0
根据这几个式子可以推出 另外两个点的坐标
剩下的就是枚举每两个多边形的每条边是否相交
就是输入输出格式要细心点
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
struct Point
{
double x,y;
Point(double x = 0,double y = 0):x(x),y(y){}
};
typedef Point Vector;
Vector operator + (Vector a, Vector b) { return Vector(a.x+b.x,a.y+b.y) ;}
Vector operator - (Vector a, Vector b) { return Vector(a.x-b.x,a.y-b.y) ;}
Vector operator * (Vector a,double p) { return Vector(a.x*p,a.y*p) ;}
Vector operator / (Vector a,double p) { return Vector(a.x/p,a.y/p) ;}
double Dot(Vector a,Vector b) { return a.x*b.x + a.y*b.y ;}
double Length(Vector a) { return sqrt(Dot(a,a)) ;}
double Cross(Vector a, Vector b) { return a.x*b.y - a.y*b.x ;}
const double eps = 1e-8;
int dcmp(double x)
{
if(fabs(x) < eps) return 0;
else return x < 0 ? -1 : 1;
}
bool operator == (Point a,Point b)
{
return dcmp(a.x-b.x) == 0&& dcmp(a.y-b.y) == 0;
}
bool operator < (Point a,Point b)
{
return a.x < b.x || (a.x == b.x && a.y < b.y);
}
bool Onsegment(Point p,Point a,Point b)
{
return dcmp(Cross(b-a,p-a)) == 0 && dcmp(Dot(b-p,a-p)) < 0 || (p == a) || (p == b);
}
bool OnLine(Point p,Point a,Point b)
{
return fabs(Cross(p-a,a-b)) / Length(b-a);
}
bool Segmentsection(Point a,Point b,Point c,Point d)
{
double d1 = Cross(b-a,c-a),d2 = Cross(b-a,d-a),d3 = Cross(d-c,a-c),d4 = Cross(d-c,b-c);
if(dcmp(d1)*dcmp(d2) < 0 && dcmp(d3)*dcmp(d4) < 0) return true;
else if(dcmp(d1) == 0 && Onsegment(c,a,b) ) return true;
else if(dcmp(d2) == 0 && Onsegment(d,a,b) ) return true;
else if(dcmp(d3) == 0 && Onsegment(a,c,d) ) return true;
else if(dcmp(d4) == 0 && Onsegment(b,c,d) ) return true;
else return false;
}
Point Segment(Point p,Vector v,Point q,Vector w)
{
Vector u = p-q;
double t = Cross(w,u) / Cross(v,w);
return p + v*t;
}
double Max(double a,double b)
{
return a > b ? a : b;
}
struct Line
{
Point s,e;
Line(Point s = 0,Point e = 0) :s(s),e(e){}
};
struct polygon
{
Point p[30];
int num;
}poly[50];
bool Ispoly(polygon a,polygon b)
{
if(a.num != 0 && b.num != 0)
{
for(int i = 0; i < a.num; i++)
{
for(int j = 0; j < b.num; j++)
{
if( Segmentsection(a.p[i],a.p[(i+1)%a.num],b.p[j],b.p[(j+1)%b.num]) )
return true;
}
}
}
return false;
}
int main()
{
char str[10],strr[20];
memset(poly,0,sizeof(poly));
while(scanf("%s",str) != EOF)
{
if(strcmp(str,".") == 0)
{
break;
}
if(strcmp(str,"-") == 0)
{
char c[30];
int k,j;
for(int i = 0; i < 26; i++)
{
k = 0;
for(j = 0; j < 26; j++)
{
if( i != j && Ispoly(poly[i],poly[j]))
{
c[k++] = j + 'A';
}
}
if(k == 0 && poly[i].num != 0)
{
printf("%c has no intersections\n",i+'A');
}
else if(poly[i].num != 0)
{
printf("%c intersects with %c",i+'A',c[0]);
if(k == 2)
{
printf(" and %c",c[1]);
}
else if(k > 2)
{
for(int m = 1; m < k-1; m++)
{
printf(", %c",c[m]);
}
printf(", and %c",c[k-1]);
}
printf("\n");
}
}
printf("\n");
memset(poly,0,sizeof(poly));
continue;
}
scanf("%s",strr);
int temp = str[0]-'A';
double x,y;
if(strcmp(strr,"square") == 0)
{
poly[temp].num = 4;
scanf(" (%lf,%lf)",&x,&y);
poly[temp].p[0].x = x, poly[temp].p[0].y = y;
scanf(" (%lf,%lf)",&x,&y);
poly[temp].p[2].x = x, poly[temp].p[2].y = y;
poly[temp].p[1].x = (poly[temp].p[0].x+poly[temp].p[2].x +poly[temp].p[2].y-poly[temp].p[0].y)/2;
poly[temp].p[1].y = (poly[temp].p[0].y+poly[temp].p[2].y+poly[temp].p[0].x-poly[temp].p[2].x)/2;
poly[temp].p[3].x = (poly[temp].p[0].x+poly[temp].p[2].x +poly[temp].p[0].y-poly[temp].p[2].y)/2;
poly[temp].p[3].y = (poly[temp].p[0].y+poly[temp].p[2].y+poly[temp].p[2].x-poly[temp].p[0].x)/2;
}
else if(strcmp(strr,"rectangle") == 0)
{
poly[temp].num = 4;
scanf(" (%lf,%lf)",&x,&y);
poly[temp].p[0].x = x, poly[temp].p[0].y = y;
scanf(" (%lf,%lf)",&x,&y);
poly[temp].p[1].x = x, poly[temp].p[1].y = y;
scanf(" (%lf,%lf)",&x,&y);
poly[temp].p[2].x = x, poly[temp].p[2].y = y;
poly[temp].p[3].x = (poly[temp].p[0].x + poly[temp].p[2].x - poly[temp].p[1].x);
poly[temp].p[3].y = ( poly[temp].p[2].y - poly[temp].p[1].y + poly[temp].p[0].y);
}
else if(strcmp(strr,"line") == 0)
{
poly[temp].num = 2;
scanf(" (%lf,%lf)",&x,&y);
poly[temp].p[0].x = x, poly[temp].p[0].y = y;
scanf(" (%lf,%lf)",&x,&y);
poly[temp].p[1].x = x, poly[temp].p[1].y = y;
}
else if(strcmp(strr,"polygon") == 0)
{
int n;
scanf("%d",&n);
poly[temp].num = n;
for(int i = 0; i < n; i++)
{
scanf(" (%lf,%lf)",&x,&y);
poly[temp].p[i].x = x, poly[temp].p[i].y = y;
}
}
else
{
poly[temp].num = 3;
scanf(" (%lf,%lf)",&x,&y);
poly[temp].p[0].x = x, poly[temp].p[0].y = y;
scanf(" (%lf,%lf)",&x,&y);
poly[temp].p[1].x = x, poly[temp].p[1].y = y;
scanf(" (%lf,%lf)",&x,&y);
poly[temp].p[2].x = x, poly[temp].p[2].y = y;
}
}
return 0;
}