DAY23：二叉树（十三）二叉树的最近公共祖先+二叉搜索树的最近公共祖先

236.二叉树的最近公共祖先

• 一定要仔细看提示，二叉树数值不重复，意味着后序遍历不会存在两边找到了同个元素的情况
• 本题需要进一步理解后序遍历，可以认为后序遍历在"深入"到每个子树的最深层之后，才开始"回溯"并访问节点。在某种意义上，这可以被视为从下往上的遍历方式，但需要注意的是，它并不是简单地按照树的层级从下往上进行遍历的。

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：
输入：root = [1,2], p = 1, q = 2
输出：1

思路

找最近公共祖先，也就是已知两个节点，从下往上去找这两个节点的最近公共祖先。

我们遍历二叉树的时候，不能从下往上去遍历。但是我们的处理顺序，是可以从下往上处理的。回溯的过程，实际上就是从底往上处理的过程。

针对某一个节点，左子树出现了p或者右子树出现了q，就把信息向上返回。实质上就是后序遍历的处理过程。

后序遍历（左右中）就是天然的回溯过程，可以根据左右子树的返回值，来处理中节点的逻辑。

思路就是后序遍历，遇到p就返回，遇到q就返回，当某个节点左右子树返回值都不为空的时候，这个节点就是最近的公共祖先。

• 注意，因为本题题目提示中说了二叉树数值不重复，所以可以不用考虑两边找到了p/q同个元素的情况

完整版

• 注意p或者q其中一个本来就是公共祖先的情况。但是这种情况其实和后序遍历处理逻辑是重合的。
• 遇到了p往上返回的时候，要注意这个题目并不是要求返回bool类型，而是要求返回最近公共祖先节点！因此，我们往上返回，应该返回的是root本身

//后序遍历，左子树返回值不为空说明有p或q，右子树同理
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //终止条件
        if(root==nullptr){
            return nullptr;
        }
        //后序，左右中
        //左
        TreeNode* left = lowestCommonAncestor(root->left,p,q);
        //右
        TreeNode* right = lowestCommonAncestor(root->right,p,q);
        //中，如果遇到了p/q就返回root，这道题目要求是root
        if(root==p||root==q){
            return root;
        }
        //如果都返回了就是最近公共祖先
        if(left!=nullptr&&right!=nullptr){
            return root;
        }
        //注意此处的逻辑！如果right存在left不存在，说明右子树里面有p/q，需要返回right，而不是root！
        if(left==nullptr&&right!=nullptr){
            return right;
        }
        if(left!=nullptr&&right==nullptr){
            return left;
        }
        //如果以上全部不满足，左是空右也是空
        return nullptr;
        
    }
};

后序遍历的进一步理解

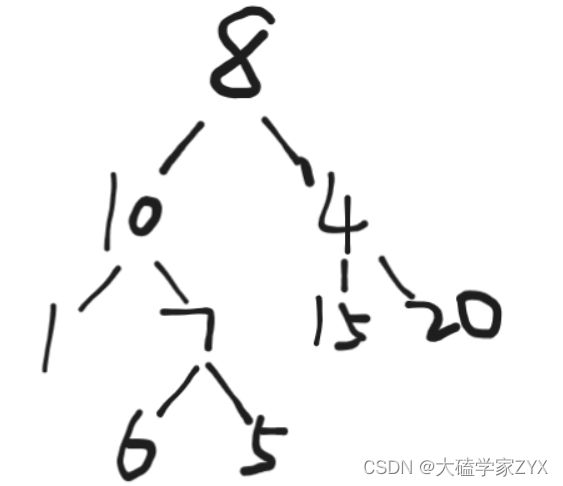
例如这个例子，后序遍历（Post-Order Traversal）的总体顺序是：(10的子树) -> (4的子树) -> 8

对于给定的二叉树，我们可以按照后序遍历的规则列出以下结果：

• 对于子树10, 1, 7, 6, 5，后序遍历的顺序是：1 -> 6 -> 5 -> 7 -> 10.
• 对于子树4, 15, 20，后序遍历的顺序是：15 -> 20 -> 4.
• 对于整个二叉树，后序遍历的顺序是：(10的子树) -> (4的子树) -> 8。

所以，这棵树的后序遍历结果是：1, 6, 5, 7, 10, 15, 20, 4, 8。

后序遍历并非从下往上遍历，而是首先遍历左孩子节点，然后遍历右孩子节点，最后遍历根节点。这个过程在每个子树中都会被重复。

因此，可以认为后序遍历在"深入"到每个子树的最深层之后，才开始"回溯"并访问节点。在某种意义上，这可以被视为从下往上的遍历方式，但需要注意的是，它并不是简单地按照树的层级从下往上进行遍历的。

这棵树的前序和中序也补充一下：

前序遍历：

• 对于子树10, 1, 7, 6, 5，前序遍历的顺序是：10 -> 1 -> 7 -> 6 -> 5。
• 对于子树4, 15, 20，前序遍历的顺序是：4 -> 15 -> 20。
• 对于整个二叉树，前序遍历的顺序是：8 -> (10的子树) -> (4的子树)。

所以，这棵树的前序遍历结果是：8, 10, 1, 7, 6, 5, 4, 15, 20。

中序遍历：

• 对于子树10, 1, 7, 6, 5，中序遍历的顺序是：1 -> 10 -> 6 -> 7 -> 5。
• 对于子树4, 15, 20，中序遍历的顺序是：15 -> 4 -> 20。
• 对于整个二叉树，中序遍历的顺序是：(10的子树) -> 8 -> (4的子树)。

所以，这棵树的中序遍历结果是：1, 10, 6, 7, 5, 8, 15, 4, 20。

为什么左为空右不为空的时候return right

如果left为空，而right不为空，说明只有右子树包含了这两个指定节点之一或者右子树包含了这两个节点的最近公共祖先，所以返回right。反之，如果right为空，而left不为空，说明只有左子树包含了这两个指定节点之一或者左子树包含了这两个节点的最近公共祖先，所以返回left。

返回的结果最终都会向上层节点传递，直到找到最近公共祖先。

这个算法基于后序遍历的原因是，我们需要检查一个节点的左右子树以确定该节点是否是两个指定节点的公共祖先，所以必须等到遍历了该节点的左右子树之后才能做出决定，这符合后序遍历的顺序：左子树 -> 右子树 -> 根节点。也和后序遍历进一步理解的本质相同，也就是先深入左右子树进行遍历，再"回溯"回根节点。

这个逻辑是否包含p/q本身就是公共祖先的情况

如果p/q本身就是公共祖先，例如下图的情况

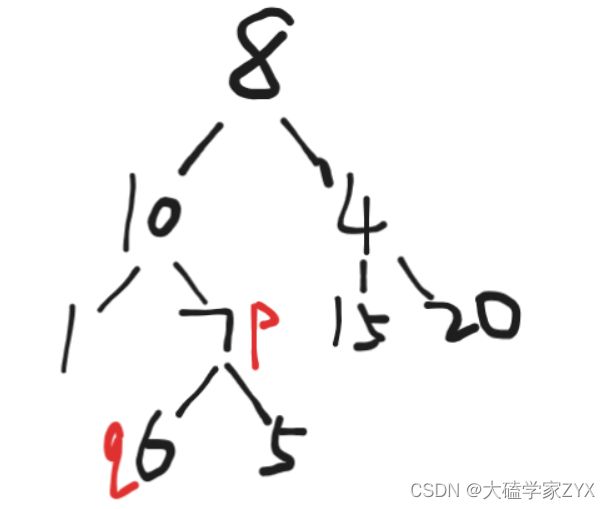
如果是图上情况，左子树不是空的，右子树是空，返回到7的时候，由于if(rootp||rootq)会判断是不是本身和p/q相等，因此此时直接返回了7，其余部分又没有p/q，因此直接一路向上返回。

这个逻辑的核心就在于，遇到了p/q直接把当前和p/q相等或满足祖先条件的节点向上返回，并且当遇到左右有一个返回值的情况，继续保留左边的返回值。但还是会优先返回和p/q相等的节点，包含了p/q本身是公共祖先的情况。

• 如果涉及到，中要根据左和右的结果来判断，一定是后序遍历。
• 将结果一层一层返回上去，涉及这个”回溯“的过程，一定是后序遍历

235.二叉搜索树的最近公共祖先

• 本题一定要注意思路的理解， 如果root的值在[p,q]之间，那么root一定是p和q的最近公共祖先！

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

思路

本题要利用二叉搜索树的特性，来找最近的公共祖先。

因为二叉搜索树是有序树，且顺序为左子树<根节点<右子树。

• 如果根节点root大于p和q的值，说明公共祖先一定在左子树里。
• 根节点root小于p和q的值，说明公共祖先一定在右子树里。
• root的值在p和q之间，说明当前节点就是p和q的公共祖先。
  • 节点值在[p,q]之间，说明p一定在节点左子树里，q一定在节点右子树里。
  • 在这种情况下，无论是向左遍历还是向右遍历，总会错过p/q其中的一个！只有当前节点，才能连接p和q！

因此，本题最重要的一点就是，如果节点root的值在p和q之间，那么节点root就是p和q的最近公共祖先！

可以画二叉树模拟一下。如果p/q分别在节点左子树和右子树里面，那么不管向哪个方向遍历，都会错过一个，不再是公共祖先了。也就是说后面不可能再有公共祖先了。

关于遍历顺序

这道题并不需要单独考虑遍历顺序的问题，因为树本身就是有序的，不需要处理中间节点所以没有中间节点的逻辑，只要有一个左和一个右就可以了！

而且本题并不涉及到单调递增的问题，不是一定要中序遍历。并没有中间节点逻辑。

递归法

最开始的写法

• 这种写法需要加很多if，代码比较冗余，debug的情况比较多
• 二叉树因为建立的时候比较麻烦，在IDE里debug不太方便，我们可以采用直接在力扣里面打印输出的方式进行调试

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //搜索树的有序性，按序排列
        if(root==nullptr){
            return nullptr;
        }
        TreeNode* right = nullptr;
        TreeNode* left = nullptr;

        //如果root小于p q 一定在右子树里
        if(root->val<p->val&&root->val<q->val){
            right = lowestCommonAncestor(root->right,p,q);
            //cout<< righ->val <
        } 
        //如果root大于p q 一定在左子树里
        if(root->val>p->val&&root->val>q->val){
            left = lowestCommonAncestor(root->left,p,q);
            //cout<< left->val <
        }
        if(root->val>p->val&&root->val<q->val){
            return root;
        }
        if(root->val>q->val&&root->val<p->val){
            cout<< root->val <<endl;
            return root;
        }
        if(root->val==p->val||root->val==q->val){
            //cout<< root->val <
            return root;
        }

       
        if(right!=nullptr&&left==nullptr){
            return right;
        }
        if(left!=nullptr&&right==nullptr){
            return left;
        }
        return nullptr;
    }
};

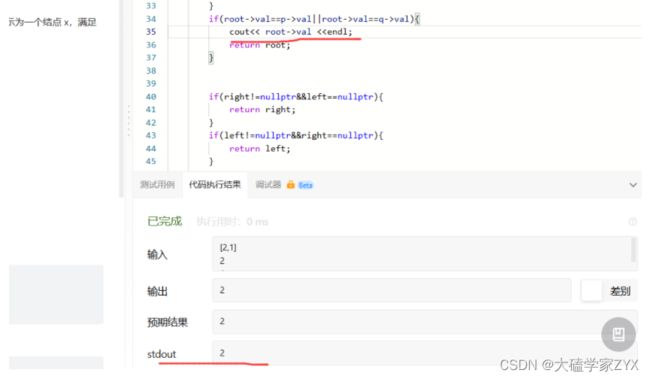
debug测试

这种较大的二叉树比较难建，直接在力扣里面打印想看的中间结果就行

修改版

因为p和q的大小关系，原题目是没有说的，所以我们最好把在PQ之间的情况放在else里面

• 核心点在于节点数值只要不为空，只有三种情况：小于p q，大于p q，其他情况全部都是我们要找的公共祖先！

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //这道题目并不需要处理中间节点，有左右就可以了
        if(root==nullptr){
            return nullptr;
        }
        //左右
        if(root->val<p->val&&root->val<q->val){
            //也可以写在if里面，写里面的话直接在里面返回
            TreeNode* right = lowestCommonAncestor(root->right,p,q);
            if(right!=nullptr){
                return right;
            }
        }
        if(root->val>p->val&&root->val>q->val){
            TreeNode* left = lowestCommonAncestor(root->left,p,q);
            if(left!=nullptr){
                return left;
            }
        }
        //夹在中间或者相等，这就是其余所有情况
        //直接return 不要写在else里面否则会被判定没有返回值
        return root;
    }
};

迭代法

最开始的写法

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //都大于的时候向左遍历
        while(root->val > p->val && root->val > q->val){
            root = root->left;
        }
        //都小于的时候向右遍历
        while(root->val < p->val && root->val < q->val){
            root = root->right;
        }
        //找到最近公共祖先
        return root;
    }
};

为什么最开始这种写法不行？

写法在一个很长的用例上发生了报错

这是因为整体写法思路错了，不能先一直往左找，再一直往右找，每走一层都要重新判断往哪里走，因为可能先左后右再左。如果是上面的while写法，就是左边一直遍历左子树的左节点，但是错过了左子树的右节点！每一层都需要重新的判断去左边还是右边。

修改版

• 注意，这里可以写while(1)，因为while里面是什么并不重要，总会跳出去！
• 最后还要写返回值是因为函数必须有一个不在if语句内的返回值，其实这里的返回值没有意义，上面一定会返回

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //这里可以写while(1)，因为while里面是什么并不重要，总会跳出去！
        //while(root!=nullptr)
        while(1)
        {
            if(root->val > p->val && root->val > q->val)
                root = root->left;
            else if(root->val < p->val && root->val < q->val)
                root = root->right;
            else
                return root;
        }
        //跳出while之后的返回值,其实这里随便写就行因为while里面一定会return
        return nullptr;
    }
};