AcWing 837. 连通块中点的数量

题目如下：

给定一个包含 n个点（编号为 1∼ n）的无向图，初始时图中没有边。

现在要进行 m 个操作，操作共有三种：

1. C a b，在点 a和点 b之间连一条边，a 和 b 可能相等；
2. Q1 a b，询问点 a 和点 b 是否在同一个连通块中，a 和 b 可能相等；
3. Q2 a，询问点 a 所在连通块中点的数量；

输入格式

第一行输入整数 n 和 m。

接下来 m 行，每行包含一个操作指令，指令为 C a b，Q1 a b 或 Q2 a 中的一种。

输出格式

对于每个询问指令 Q1 a b，如果 a 和 b 在同一个连通块中，则输出 Yes，否则输出 No。

对于每个询问指令 Q2 a，输出一个整数表示点 a 所在连通块中点的数量

每个结果占一行。

数据范围

1≤n,m≤10^5
 

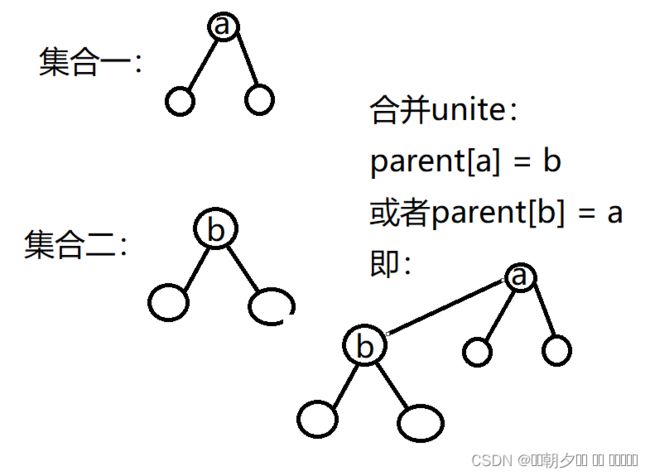
思路：采用并查集数据结构

定义一个祖先数组parent（初始化为下标值，这里从1开始）和一个记录集合结点数的数组size（初始化为1）

 

parent.resize(n + 1);
size.resize(n + 1, 1);
for (int i = 1; i <= n; i++) {
    parent[i] = i;
}

void unite(int x, int y){
    int rootX = find(x);
    int rootY = find(y);
    if(rootX != rootY){
        if(size[rootX] < size[rootY]){
            parent[rootX] = rootY;
            size[rootY] += size[rootX];
         }else {
             parent[rootY] = rootX;
             size[rootX] += size[rootY];
         }
     }
}

查找find操作（查找该集合处在哪个集合中）：当parent[a] != a,则表示集合a还有父节点，则令parent[a] = find(parent[a]),若还是不相等，重复上述操作，直到相等，则找到了该集合的根

int find(int x){
    if(parent[x] != x)  parent[x] = find(parent[x]);
    return parent[x];
}

判断两个集合是否在同一集合中的操作isConnect:当两个集合在同一集合中，则他们的根是相同的

bool isConnected(int x, int y){
    return find(x) == find(y);
}

获取结点数getSize：（size值在每一次合并时，都会更新）

int getSize(int x){
    return size[find(x)];
}

完整代码如下：

#include 
using namespace std;

class UnionFind{
    private:
        vector parent;
        vector size;
    public:
        UnionFind(int n) {
            parent.resize(n + 1);
            size.resize(n + 1, 1);
            for (int i = 1; i <= n; i++) {
                parent[i] = i;
            }
        }

        int find(int x){
            if(parent[x] != x)  parent[x] = find(parent[x]);
            return parent[x];
        }
        
        void unite(int x, int y){
            int rootX = find(x);
            int rootY = find(y);
            if(rootX != rootY){
                if(size[rootX] < size[rootY]){
                    parent[rootX] = rootY;
                    size[rootY] += size[rootX];
                }else {
                    parent[rootY] = rootX;
                    size[rootX] += size[rootY];
                }
            }
        }
        
        bool isConnected(int x, int y){
            return find(x) == find(y);
        }
        
        int getSize(int x){
            return size[find(x)];
        }
};

int main(){
    int n, m;
    cin >> n >> m;

    UnionFind uf(n);

    for (int i = 0; i < m; i++) {
        string op;
        int a, b;
        cin >> op >> a;
        if (op == "C") {
            cin >> b;
            uf.unite(a, b);
        } else if (op == "Q1") {
            cin >> b;
            if (uf.isConnected(a, b)) {
                cout << "Yes" << endl;
            } else {
                cout << "No" << endl;
            }
        } else if (op == "Q2") {
            cout << uf.getSize(a) << endl;
        }
    }
    return 0;
}