Graph Neural Architecture Search

背景

自动设计网络架构，提出了一种基于强化学习的图神经结构搜索方法（GraphNAS），该方法能够自动设计最佳的图神经结构。这是首次尝试研究使用强化学习设计最佳图形神经结构这一具有挑战性的问题。设计了一个新的搜索空间，覆盖来自最先进GNN的算子，并使用策略梯度算法迭代求解该问题。神经架构搜索可以通过搜索空间，搜索策略，性能评估策略得到比人工搭建的模型更优的性能。图神经架构搜索网络通过自动定义更好的性能。

Gao Y, Yang H, Zhang P, et al. Graph Neural Architecture Search[C]//IJCAI. 2020, 20: 1403-1409.

模型

神经架构搜索概述

   神经架构搜索 (Neural Architecture Search)[1]， 简称为NAS。对比于超参优化的区别，超参优化是自动调优训练参数，神经架构搜索是调优定义网络结构的参数。一般地，深度学习网络结构包含的超参数一般有定义的网络结构参数，例如网络层数，卷积核的尺寸。除此之外，深度学习网络结构包含的超参数有相关优化的超参数，例如学习率，批量训练时样本的大小，权重衰减等。其它关于深度学习网络结构的参数有正则化系数等。

  神经架构搜索通常由搜索策略，搜索空间，性能评估策略三部分组成。神经架构搜索主要通过搜索策略在搜索空间中进行搜索，搜索性能的好坏主要通过性能评估策略进行评估。通过神经架构搜索得到满足任务需求并且较优的网络结构。

  搜索策略：搜索策略有通过进化算法进行搜索，通过强化学习进行搜索，通过梯度优化以及贝叶斯的方法进行搜索优化。进化算法又称为演化算法，遗传算法是一种最基本的进化算法。遗传算法中，种群中的每个变量都是在优化算法解空间中的最优解。一般地，遗传算法通过模拟物种的进化过程在来求解最优解。通过强化学习进行搜索的算法，是一种基于梯度的方法寻找最优架构。强化学习又叫做增强学习，是从动物学习等自适应学习等理论发展起来的。参数选择一个动作，应用于一个环境，环境会因为接收到的动作，引起状态发生变化。除此以外，环境会产生一个反馈给参数，参数会依据反馈重新选择动作。除此以外，基于梯度策略和贝叶斯优化的方法可以应用到神经架构搜索中。

  搜索空间：神经架构的搜索空间一般称为可选择的神经网络结构的集合。

  性能评估策略：神经架构搜索的度量指标有精度，以及速度来进行度量。

图神经架构搜索模型

  图神经架构搜索 (Graph Neural Architecture Search)[2]，是一种基于强化学习搜索策略的算法，简称为GraphNAS。 搜索空间采用图神经网络前沿的运算操作，例如图卷积神经网络 (GCN), 大图上的归纳表示学习 (GraphSage)，图注意力网络 (GAT)。

  搜索空间主要包括采样，卷积，信息聚合，多头和读操作。采样操作是对邻域进行采样。 GraphSage对大图进行采样时，一般通过固定邻域大小的方法进行采样。 卷积操作一般是指当前节点$u$与邻接节点$v$进行卷积操作，节点$u$与节点$v$之间的关系表示为$ {e_{uv}}$。在卷积操作中加入边的关系表示为$\footnotesize Fun({{\bf{h}}_u},{{\bf{h}}v}){e{uv}}$。通过上述操作，可以在进行节点与节点的特征融合后，再进行与边特征信息融合。信息聚合的操作可以通过最大聚合$\footnotesize max( \cdot )$，最小值聚合$\footnotesize min( \cdot )$，求和$\footnotesize sum( \cdot )$的方式进行，除上述聚合方式外，还可通过神经网络进行特征映射。多头操作与注意力机制相关，可将注意力机制重复$k$ 次， $k$ 则表示多头的头数。在GraphNAS 的搜索空间中，$k\in \{1,2,4,6,8,16\}$ ，输出维度$d\in \{8,16,32,64,128,256,512\}$ 。 在GraphNAS 中，激活函数使用了$sigmoid(\cdot )$ ，$tanh(\cdot )$ ，$relu(\cdot )$ ，$identity(\cdot )$ ，$softplus(\cdot )$ ，$leaky\_relu(\cdot )$ ，$relu6(\cdot )$ ，$elu(\cdot )$ 。

给定一个图神经架构搜索空间$\mathcal{S}$ ，验证集集合 $\mathrm{D}$。在验证集 $\mathrm{D}$ 上，优化函数的目标为优化得到一个最好的架构使得验证集$\mathrm{D}$ 的准确率最高。将最优化的架构描述为 $s^{\ast }$。一般地， $s^{\ast }$表示为:

$$s^{\ast }=\arg \underset{s\in \mathcal{S}}{\max }\mathbb{E}[R_D(s)]\text{\hspace{1em}(1)}$$

上述公式表示通过采样架构 $s$，求使得奖赏期望最大化的最优架构$s^{\ast }$。通过强化学习可计算上述公式中的奖赏。

  在GraphNAS中，层数$L$设置为两层，可以减小搜索空间，提高搜索效率。在Graph-NAS中，节点之间的系数计算方式可以表述为：当两个节点之间存在关系，则表示为1。由于单个节点的邻居节点可能有多个，因此引入度。节点$u$的度表示为$d_u$，节点$v$ 的度表示为$d_v$，则两个节点之间的系数表示为$\footnotesize 1/\sqrt {{d_u}{d_v}} $。类似地，在图注意力机制中，两个节点之间的系数可以通过特征映射与激活函数组成，表示为$\footnotesize e_{uv}^{gat}$

$$e_{uv}^{gat}=leaky\_relu({\mathbf{w}}_l^{\mathrm{T}}{\mathbf{h}}_u+{\mathbf{w}}_r^{\mathrm{T}}{\mathbf{h}}_v)\text{\hspace{1em}(2)}$$

对称的注意力注意力机制中，两个节点之间的系数可以表示为$e_{uv}^{gat}+e_{vu}^{gat}$。除此以外，两个节点之间的系数还可以表示为基于余弦的，基于线性的和一般线性的。基于余弦的系数表示为$ \footnotesize < {\bf{w}}_l^{{\rm{T}}*{{\bf{h}}_u},{\bf{w}}_r}{\rm{T}}{{\bf{h}}_v} > $，基于线性的系数$\footnotesize \tanh (sum({\bf{w}}_l^{\rm{T}}*{{\bf{h}}_u}))$，一般线性的系数表示为:

$${\mathbf{w}}_l^{\mathrm{T}}leaky\_relu({\mathbf{w}}_l\ast {\mathbf{h}}_u+{\mathbf{w}}_r\ast {\mathbf{h}}_v)\text{\hspace{1em}(3)}$$

在神经架构搜索算法中，除了定义搜索空间外，还需要更好的搜索算法进行迭代优化，得到最终的优化结构。GraphNAS的搜索算法中采用了强化学习的算法。强化学习是一种累积奖赏最大化的优化策略算法。由于网络的组成是一个顺序连接的序列，因此RNN用来预测操作的序列。 在GraphNAS 中，采用了策略梯度的优化算法更新RNN中的参数。RNN则做为控制器生成适应于数据集的最好的架构。除此以外， GraphNAS使用验证集上的精度做为奖赏信号。

GraphNAS在进行架构搜索时的具体步骤如下：步骤一：使用搜索空间中的操作设计架构$s$；步骤二：在$s$上训练网络；步骤三：计算奖赏信号；步骤四：依据奖赏信号更新控制器RNN中的参数。训练的损失使用交叉熵损失函数。

$${\nabla }_{\theta }{\mathbb{E}}_{P(s_{1:T};\theta )}[R]=\sum _{t\in T}{\mathbb{E}}_{P(s_{1:T};\theta )}[{\nabla }_{\theta }logP(s_t|s_{t-1};\theta )(R-b)]\text{\hspace{1em}(4)}$$

$b$通过之前搜索得到的架构计算得出，$R$是当前计算得出的奖赏。$s_i$ 是从搜索空间$\mathcal{S}$中采样的结构，$\theta$是RNN中的模型初始化的参数。

论文内容

使用的相关操作：

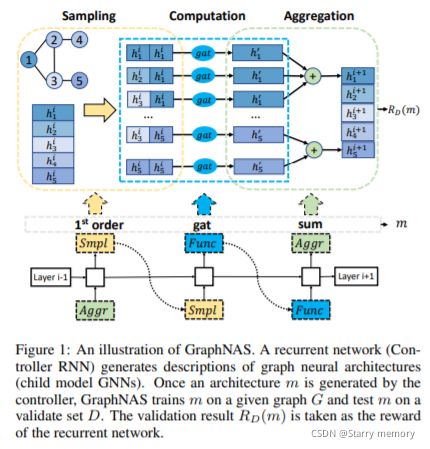
独立地搜索GCN的各层layer以减少搜索空间大小。

结果被用来更新强化学习。
$$m^{\ast }=\arg \underset{m\in \mathcal{M}}{\max }\mathbb{E}\left[R_D(m)\right]$$

controller是不可微的，所以使用强化学习来做参数更新

这个图可以和上面的图对应着看，颜色对应。

代码

在搜索空间中进行搜索

self.search_space = {
    "attention_type": ["gat", "gcn", "cos", "const", "gat_sym", 'linear', 'generalized_linear'],
    'aggregator_type': ["sum", "mean", "max", "mlp", ],
    'activate_function': ["sigmoid", "tanh", "relu", "linear",
                          "softplus", "leaky_relu", "relu6", "elu"],
    'number_of_heads': [1, 2, 4, 6, 8, 16],
    'hidden_units': [4, 8, 16, 32, 64, 128, 256],
}

测试搜索的效果

训练打印结果，这是超参数

 self.args.lr = param[0]
 self.args.in_drop = param[1]
 self.args.weight_decay = param[2]
 self.args.num_hidden = param[3]
'hyper_param': [0.01, 0.9, 0.0001, 64]}

100次然后再来一个100次迭代，最终得到有用的结果

https://github.com/GraphNAS/GraphNAS

代码解读

controller对应的代码在graphnas/graphnas_controller.py

controller_hid设定为超参数设定为100

self.encoder 的shape is [所有动作类型数，controller_hid]
self._decoder是一个字典，每个key为搜索空间中的类型，shape is [key, controller_hid， size(搜索空间中每个动作类型的数量)]

参考文献

1. Neural Architecture Search with Reinforcement Learning， ICLR, 2017.
2. Graph Neural Architecture Search，IJCAI，2020.