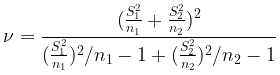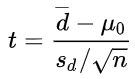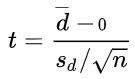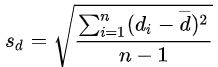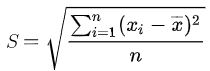t检验.医学统计实例详解
t检验是医学统计学中常用的一种假设检验方法,用于比较两个样本均值是否有显著差异。它可以帮助医学研究者确定一个治疗方法或药物是否显著地改善了患者的症状或生理指标。
在医学研究中,t检验常被用来:
- 比较两个独立样本的均值:例如,比较一个治疗组和一个对照组的平均响应时间或血压。
- 比较两个配对样本的均值:例如,比较同一个人在治疗前后的血糖水平。
- 比较一个样本的均值与一个已知的总体均值:例如,比较一个新药物的平均有效期和已知的平均有效期。
在使用t检验时,需要注意:
- 样本数据必须是正态分布或接近正态分布,可以通过观察样本数据的直方图或使用正态概率图来判断。
- 样本数据的方差要相等,可以通过方差齐性检验来判断,如果方差不相等需要使用t’检验。
- t检验只能检验两个样本之间的差异,无法检验多个样本之间的差异。
一、独立样本t检验
独立样本t检验是一种常用的医学统计方法,它用于比较两组独立个体的连续变量测量结果是否存在显著差异。
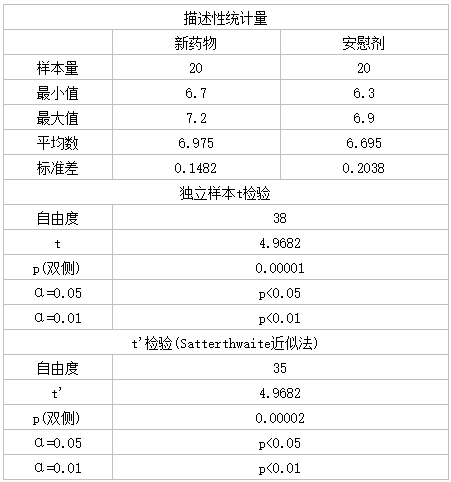
假设我们随机选择了40名失眠患者,其中20人接受了新药物治疗,另外20人接受了安慰剂治疗。我们记录了他们使用药物/安慰剂后每晚的睡眠时间,并使用独立样本t检验进行分析。
数据如下:睡眠时间(小时)
新药物
7.0,7.1,6.8,7.1,6.9,7.1,6.8,6.7,6.9,7.2,7.0,6.8,7.1,6.9,7.1,6.8,7.0,6.9,7.2,7.1
安慰剂
6.5,6.8,6.9,6.4,6.7,6.9,6.9,6.3,6.4,6.9,6.9,6.6,6.8,6.5,6.6,6.7,6.9,6.5,6.8,6.9
1、建立假设检验,确定检验水准。
H0:μ1=μ2,即新药物治疗和安慰剂治疗睡眠时间总体均数相等
H1:μ1≠μ2,即新药物治疗和安慰剂治疗睡眠时间总体均数不等
α=0.05
2、检验是否符合正态分布
使用矩法正态分布检验,在α=0.05水准下符合正态分布。
3、做方差齐性检验
使用F检验进行方差齐性检验,F=1.891,p=0.1741,p>0.1,认为方差相等。
4、计算t检验
方差相等的独立样本t检验公式
自由度=n1+n2-2
经计算:t=4.9682,p=0.00001,按α<0.05水准拒绝H0,接受H1,差异有统计学意义。可以认为新药物治疗和安慰剂治疗睡眠时间总体均数不同,新药物治疗效果好于安慰剂。
如果经过方差齐性检验,认为方差不同,就需要使用近似t检验。
近似t检验有Cochran&Cox近似t检验、Satterthwaite近似t检验和Welch近似t检验。
以Satterthwaite近似t检验为例
Satterthwaite近似t检验公式:
自由度:
二、配对样本t检验
配对样本t检验是一种常用的医学统计方法,它用于比较同一组个体在两个不同时间点或不同处理下的连续变量测量结果。
一项研究调查了某种新型药物对肥胖患者的降重效果。研究招募了10名肥胖患者,并在治疗前和治疗后分别测量了他们的体重。每个患者在治疗前和治疗后均被要求进行空腹体重测量。研究数据如下表所示:
| 患者编号 | 体重(治疗前) | 体重(治疗后) |
| 1 | 80.3 | 79.5 |
| 2 | 89.2 | 85.1 |
| 3 | 78.9 | 75.5 |
| 4 | 87.6 | 83.2 |
| 5 | 92.1 | 89.3 |
| 6 | 85.6 | 85.2 |
| 7 | 90.5 | 86.8 |
| 8 | 86.7 | 84.2 |
| 9 | 82.3 | 81.1 |
| 10 | 91.8 | 88.6 |
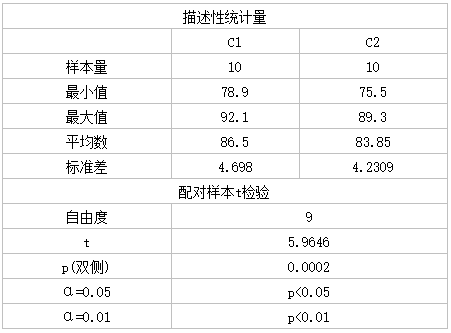
本实例中的数据采用了配对样本设计,因为每个患者在治疗前和治疗后的体重是互相对应的。因此,我们需要使用配对样本t检验来比较治疗前和治疗后体重的差异。
建立假设检验,确定检验水准。
H0:μ1=μ2,治疗前和治疗后体重没有显著差异
H1:μ1≠μ2,治疗前和治疗后体重有显著差异
α=0.05
配对样本t检验公式:
即
其中
自由度
![]()
经计算,t=5.9646,p=0.0002,p<0.05,因此我们可以拒绝H0,接受H1,即治疗前和治疗后体重有显著差异,治疗后体重平均数小于治疗前体重平均数,说明新型药物对肥胖患者的降重效果显著。
三、单样本t检验,比较一个样本的均值与一个已知的总体均值
通过大规模调查,已知某地女性的平均体重为59kg,为研究某种药物是否会影响体重,从服药女性中随机选取30人,记录了她们的体重。数据如下(单位:kg):
64,58,60,53,62,69,53,70,63,53,64,61,59,55,68,69,59,65,58,63,57,68,66,61,67,60,63,66,69,53。
建立假设检验,确定检验水准。
H0:μ1=μ2,服药女性体重与总体女性体重没有显著差异
H1:μ1≠μ2,服药女性体重与总体女性体重有显著差异
α=0.05
单样本t检验公式:
其中
自由度
![]()
经计算,t=2.9573,p=0.0061,p<0.05,因此我们可以拒绝H0,接受H1,即服药女性体重与总体女性体重有显著差异。这意味着该药物会增加服药女性体重。
(t检验.医学统计实例详解 - 天兰统计-医学统计助手★卡方检验,t检验,F检验,秩和检验,方差分析)