RTKLIB模糊度固定模式介绍以及部分模糊度固定技术（附源码，基于RTKLIB）

模糊度固定简述

伪距从名称上来看，其实是一个距离，虽然该“距离”含有误差以及随机噪声较大；但接收机在第一次跟踪载波时，只能明确知道其初始相位，在信号传播过程中的周期数是没有办法明确知道的，而这个周期数就是我们要确定的模糊度。

虽然伪距精度相对较低，但多历元滤波甚至卫星数足够情况下的单历元解，也可以达到模糊度固定的门槛。 经站星双差的模糊度，可以消除绝大部分误差，比如站间单差可消除绝大部分的大气误差以及卫星轨道、钟误差；星间单差可以消除硬件通道时延相关的误差。双差后的模糊度已经恢复其整数特性，使用lambda搜索并通过ratio检验的话，回代即可计算得到模糊度固定解，达到厘米定位精度。

但是考虑到参考卫星的变换，我们在估计参数时并不是直接估计双差模糊度。如rtklib中的设计那样，状态量中估计的是站间单差模糊度，在进行模糊度固定时再进行星间单差。

rtklib中的模糊度固定模式以及实现

rtklib中共有三种模糊度固定模式：

continuous

个人称之为 滤波模式

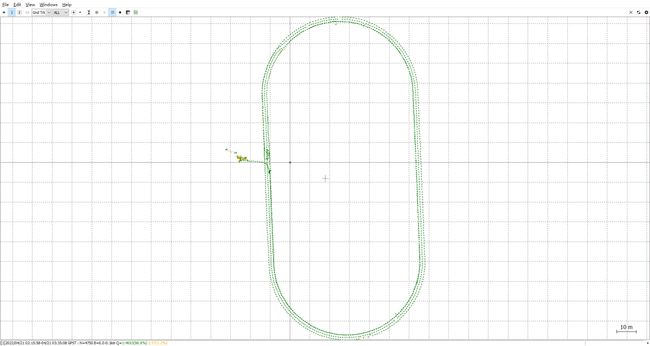
这是经典的模式，基本上提到的kalman滤波的论文，都是此模式。即相邻历元的无周跳模糊度给与一个极小的过程噪声。 但如果你用该模式跑自己采的动态数据，会发现固定率不太稳定，有时可能比较高，但大部分情况可能固定率相对较低。比如下图中，使用某同学采集的操场数据，不存在遮挡，开启所有系统并只使用第一个频点参与定位，固定率仅有1.3%，固定率低到不可思议。即使增加第二、三频点，固定率依然不乐观。 为什么该模式这么差，可能原因是rtklib数据预处理不够完善，浮点解精度很差。

instantaneous

单历元模式

该模式中相邻历元模糊度没有相关性，如果定位模式未选择PVA模式的话，相邻历元的所有状态量均不存在相关性，即每个历元做一个最小二乘，然后直接就去尝试固定模糊度。 单历元模式的优势，就是本历元结果仅与当前历元有关，不需要考虑周跳处理问题，不需要考虑滤波发散问题。当然，仅与当前历元有关，这也是它的劣势，未充分利用历元间的相关性。 与上一小节完全一致的配置，只是将模糊度固定模式进行更改，模糊度固定率惊人的达到了94%。

​

fix and hold

hold模式

该模式是在滤波模式的基础上，如果模糊度固定正确，即会将固定的模糊度约束浮点滤波器。当然，如果模糊度错误固定，会导致浮点解出现较大偏差，导致较长时间的无法固定。

部分模糊度固定技术

部分模糊度固定，其实与上一小节提到的固定模式没有关系，任何一个模式都可以使用部分模糊度固定。 如果熟悉rtklib，就知道其模糊度固定时，直接将模糊度全集进行搜索，如果无法通过ratio检验则判定固定失败，结束固定流程，然后输出模糊度浮点解。

当然，我们可以在配置文件中通过设置参与固定的卫星的高度角，来筛选参与固定的卫星，但一个历元依然只会尝试一次固定，部分模糊度固定技术就是在一个历元中进行多次模糊度固定的尝试，通过优选模糊度子集来进一步提升模糊度固定成功率。

流程如下：

如果我们认为卫星高度角越高的卫星，其模糊度的精度以及被固定成功的概率更高，那么在选择固定的模糊度子集时，就可以将卫星高度角较高的卫星最后删除，优先删除高度角较低的卫星。 原理很简单，基于rtklib实现需要熟悉其固定的流程，尤其是站间单差模糊度转站星双差模糊度的实现流程，在此不在展开。

代码实现

首先在ssat_t结构体中，针对单个卫星每个频率增加以下标识，用来进行模糊度子集选取。

uint8_t amb_flag[NFREQ]; /* ambiguity fix flag (0/1:no need to fix,2:try to fix,3: fix ref sat 4: fix) */
double amb_weight[NFREQ]; /* ambiguity weight for partial ambiguity resolution  */

同时，使用卫星的高度角进行填充，同时考虑到大部分消费级模组第一频点观测值都相对比较充足，所以我们提升了第一频点的权重，优先删除其他频点的模糊度信息。

static void fillup_amb_weight_flag(rtk_t *rtk)
{
    int i, j, na = rtk->na;
    for (i = 0; i < MAXSAT; i++)
    {
        /* check the system to fix */
        int sys = satsys(i+1, NULL);
        if (sys == SYS_GLO && rtk->opt.glomodear == 0)
        {
            continue;
        }
        if (sys == SYS_CMP && rtk->opt.bdsmodear == 0)
        {
            continue;
        }
        for (j = 0; j < NFREQ; j++)
        {
            if (rtk->x[na + j * MAXSAT + i] == 0.0 ||
                !rtk->ssat[i].vsat[j] || !rtk->ssat[i].half[j])
            {
                continue;
            }
            if (rtk->ssat[i].lock[j] < 0 || (rtk->ssat[i ].slip[j] & 2) ||
                rtk->ssat[i].azel[1] < rtk->opt.elmaskar)
            {
                continue;
            }
            /* We simply use the elevation as the amb weight, future extend to other feature */
            rtk->ssat[i].amb_weight[j] = rtk->ssat[i].azel[1] * R2D;
            if (j == 0)
            {
                /* give more weight to L1 frequency */
                rtk->ssat[i].amb_weight[j] += 35.0;
            }
            rtk->ssat[i].amb_flag[j] = 2;
        }
    }
}

增加部分模糊度的主逻辑，该逻辑会调用rtklib原始的resamb_LAMBDA函数，代码如下：

/* partial resolve integer ambiguity by LAMBDA ---------------------------------------*/
static int resamb_partial(rtk_t *rtk, double *bias, double *xa) 
{
    int i, j;

    /* reset the ambiguity flag and weight */
    for (i = 0; i < MAXSAT; i++)
    {
        for (j = 0; j < NFREQ; j++)
        {
            rtk->ssat[i].amb_flag[j] = 0;
            rtk->ssat[i].amb_weight[j] = 0.0;
        }
    }
    fillup_amb_weight_flag(rtk);
    
    /* iteration for partial resolution */
    int nb = 0;
    while ((nb = resamb_LAMBDA(rtk, bias, xa)) <= 0)
    {
        /* find the min amb weight and mark */
        double min_weight = 999.9;
        int sat_idx = -1, freq_idx = -1;
        for (i = 0; i < MAXSAT; i++)
        {
            for (j = 0; j < NFREQ; j++)
            {
                if (rtk->ssat[i].amb_flag[j] >= 2)
                {
                    if(rtk->ssat[i].amb_weight[j] < min_weight)
                    {
                        min_weight = rtk->ssat[i].amb_weight[j];
                        sat_idx = i;
                        freq_idx = j;
                    }
                }
            }
        }
        if(sat_idx >=0 && freq_idx >= 0)
        {
            rtk->ssat[sat_idx].amb_flag[freq_idx] = 1;
        }

        /* check if have enough satellites to fix */
        if (sat_num_of_to_fix(rtk) <= 5)
        {
            return 0;
        }
    }
    return nb;
}

当然，将resamb_LAMBDA函数中的ddidx函数进行了更改，更改为：

/* index for SD to DD transformation matrix D 
 * in this function, we use the ssat->amb_flag and ->amb_weight to 
 * select the ref satellite and to select the ambiguity subset to fix
 * */
static int ddidx_with_amb_weight_flag(rtk_t *rtk, int *ix)

具体该函数实现，见源码。

测试结果

使用上一小节 instantaneous模式的配置，开启部分模糊度固定的逻辑，固定率从94%提升到接近99%。

代码

公众号后台回复 git 获取码云地址，clone到本地后请切换到rtk分支查看。

公众号

有时会将代码 或者资源放在个人公众号上，有问题，在公众号后台回复，也回答的比较快一些，欢迎关注 GNSS和自动驾驶