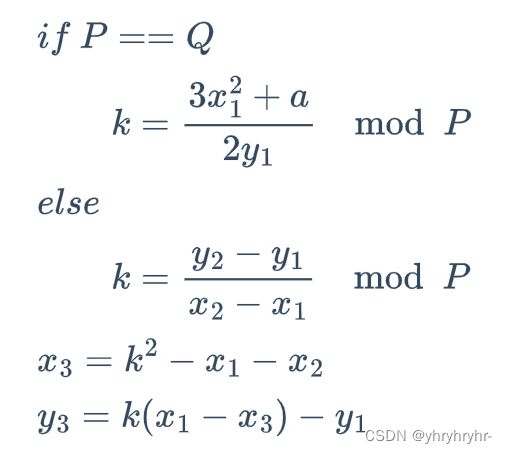yhryhryhr-

网络安全复习

低层协议安全性

IP协议

ARP协议

TCP协议

NAT协议

单钥加密体制

DES算法

课后习题

双钥加密体制

怎么说

欧几里得算法求逆

RSA算法

椭圆曲线加密

Diffie- Hellman 密钥交换算法

ElGamal签名机制

Schnorr签名机制

DSS签名算法——DSA

低层协议安全性

IP协议

对于网络层，IP协议是其中一个非常重要的协议。网络层的IP地址相当于数据链路层的Mac地址。协议字段如下，每行4字节，总共4*5=20字节。

IP协议安全性：IP协议不能保证数据就是从数据包中给定的源地址发出的，你绝对不能靠对源地址的有效性检验来判断数据包的好坏。

ARP协议

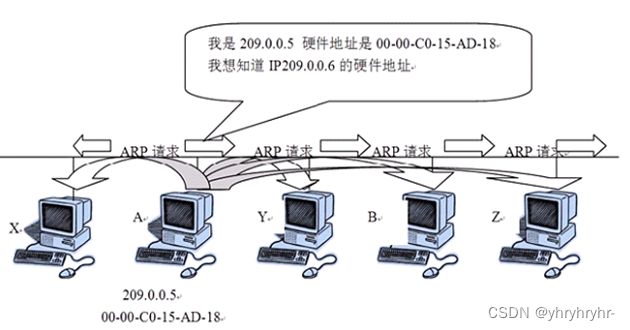
接上文，Mac地址是电脑出场自带并不可更改的；而网络环境改变了IP地址也会改变，因此需要寻找设备的IP地址。假设主机A和B在同一个网段：

A的ARP缓存表中如果有B的表项，则对IP数据包进行帧封装，单播发送给B的Mac地址。

如果没有，则如下图形式进行广播，并将得到的信息存入ARP缓存表以便下次使用。所以ARP协议中文为地址解析协议。

当ARP在不同的局域网中进行运行的时候：

主机A先把自己的IP地址与目的主机的IP地址相与，发现不在同一个子网中。
主机A便运行ARP缓存表获取默认网关的MAC地址，与默认网关进行数据帧的传送。
当运行到路由器时，路由器查询转发表，看是否转发表中有目的IP 地址，如果有的话便可以进行直接交付；没有则运行ARP协议获取下一跳路由器接口的Mac地址。
路由器接到分组后，查询转发表，将分组进行转发。

ARP协议的安全问题：一台不可信赖的主机会发出假冒的ARP查询或应答信息，并将所有流向它的数据流转移。这样，它就可以伪装成某台机器，或修改数据流。这种攻击叫做ARP欺骗攻击。

TCP协议

TCP消息格式：

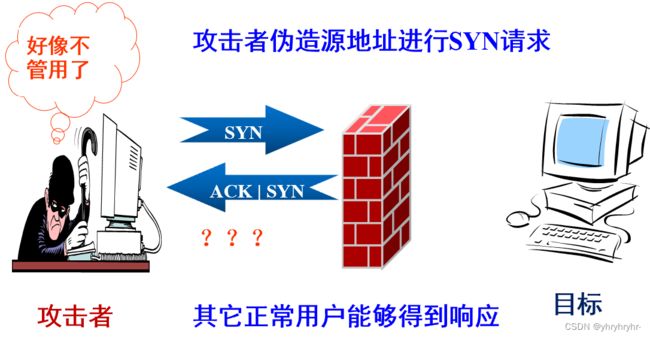
TCP连接的建立需要3次握手，当服务器收到初始的SYN数据包后，该连接处于半开放状态。此后，服务器返回自己的序号，并等待确认。最后，客户机发送第3个数据包使TCP连接开放，在客户机和服务器之间建立连接。

但处于半开放状态会消耗服务器的大量资源，所以诞生了泛洪攻击，即通过模拟IP或僵尸网络的方式大量发出第一次握手，而不回复第三次握手，大量占用服务资源。

泛洪攻击的防治有如下两种方法：

方法1（SYN Defender）：防火墙收到客户端的SYN包时，直接转发给服务器；防火墙收到服务器的SYN/ACK包后，一方面将SYN/ACK包转发给客户端，另一方面以客户端的名义给服务器回送一个ACK包，完成TCP的三次握手，让服务器端由半连接状态进入连接状态。当客户端真正的ACK包到达时，有数据则转发给服务器，否则丢弃该包。由于服务器能承受连接状态要比半连接状态高得多，所以这种方法能有效地减轻对服务器的攻击。

方法2（SYN proxy）：防火墙在收到客户端的SYN包后，并不向服务器转发而是记录该状态信息然后主动给客户端回送SYN/ACK包，如果收到客户端的ACK包，表明是正常访问，由防火墙向服务器发送SYN包并完成三次握手。这样由防火墙做为代理来实现客户端和服务器端的连接，可以完全过滤不可用连接发往服务器。

NAT协议

NAT协议的诞生主要为了解决IPV4中IP地址不足的问题。NAT协议中文全称为网络地址转换，即将一大批主机由NAT路由器都封装在一个局域网内，并赋予一个内网IP和外网IP。内网通信随意，IP地址足够；当访问外网时步骤如下（内部主机（192.168.10.1）要向外部主机（地址为210.10.20.20）发送一个数据包）：

向NAT路由器发送数据包，源地址为192.168.10.1，目的地址为210.10.20.20。
NAT路由器在转换表中增添一个条目，内部地址192.168.10.1，外部地址210.10.20.20。
NAT路由器用自己的地址（即201.26.7.9）替换数据包中的源地址，并利用路由机制，将此数据包发送给Internet上的目标主机。此时源地址就变为了201.26.7.9。
目的地址收到信息并返回响应数据包，响应数据包的源地址为210.10.20.20，而目的地址为201.26.7.9。
该响应数据包到达NAT路由器。因为响应数据包中的目的地址与NAT路由器的地址匹配，所以NAT路由器查询转换表，以确认此转换表中是否含有外部地址为210.10.20.20的条目。于是就找到了内部主机192.168.10.1。
NAT路由器用内部主机地址（即192.168.10.1）替换数据包的目的地址，并将该分组发给该内部主机。

然而，如果有多个内网主机希望与外网的同一台主机通信怎么办？

那么需要修改NAT转换表，新加几列新的参数。

内部端口	外部端口	NAT端口
标识内部主机应用程序所使用的端口号	标识某一应用程序所使用的端口号	一个依次递减的数字，由NAT路由器生成

NAT协议的安全问题：NAT最严重的问题是它不能与加密协调工作。第一，NAT不能对加密的数据流进行检查；第二，IPsec与NAT会产生冲突。

单钥加密体制

DES算法

DES属于对称密码算法中的分组加密（块加密），和流密码相对应。DES算法将明文分为若干个64位块（不足补充），秘钥为56位（8位校验位）。DES算法流程图如下

接下来，进行DES算法关键步骤的逐步解析：

IP置换

IP置换和IP逆置换，还有后面提到的P置换逻辑都是一样的。例如下图IP置换矩阵的第一行第一列为58，含义即为将第58个元素位置换为第一个。置换完后密文长度不变，仍为64位。

E扩展

64位字段可以分为前32位和后32位，前32位不变，后32位进行E扩展置48位，具体扩展方法如下：

例如图中原本的32位字段为，将32位字段分为8组，每组前后各加两个比特，组成新的 6 × 8 = 48 位字段。新加的两位分别是前一组字段的最后一位和后一组字段的第一位，见下所示。

1101 0001 0011 0100 原文本

011010 100010 100110 101001 E扩展文本

S盒压缩

S盒是精心设计的8个矩阵，是DES算法中混淆的关键部分，他的质量（随机性）很大程度影响DES的加密效果。

之后，我们要再将E扩展后的48位后半字段，通过S盒压缩为32位，具体压缩方法如下：

先将48位分为8组，每组6位。6位取出前两位和中间四位，拼成2进制数，再将2进制转化为十进制，即经过一系列操作，将6位数变为2个十进制数。将这两个十进制数当作横纵坐标，寻找S盒中对应的十进制数，再将这个十进制数用4位2进制表示。至此，我们将48位文本压缩为了32位。

(3，15)在S盒中对应的元素为13（查表得），之后转换为二进制1011，所以通过S盒我们将111111压缩为了1011。

P盒置换

P盒压缩和IP置换思路大致相似，例如第一行第一列元素为16，即将第16位置换到第一位，剩余以此类推。

秘钥生成

秘钥生成思路流程图如下：

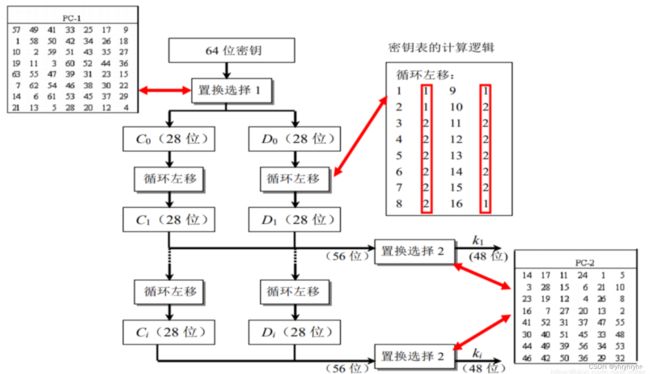如图中的流程，首先需要进行一次PC-1的选择置换，即去掉密钥中的校验位（8,16，...，64）。去掉8位校验位还剩下56位密钥，将56位分为C_0 (前28位)和D_0 (后28位) ，根据下表进行密钥的循环左移（如图中密钥表的计算逻辑）。得到的C_i D_i 进行合并后，再进行一次PC-2的选择置换，将密钥流变为48位。

Feistel结构及证明

如图可见，只要密钥倒置就可以解密密文。数学证明如下：

加密过程是：明文，进行n轮迭代。

按下列规则计算，1≤i≤n，轮函数为F

$LE_i = RE_{i-1}$

$RE_i = LE_{i-1}\bigoplus F(RE_{i-1},K_i)$

进行n轮迭代运算后，得LE_n和RE_n，输出密文

解密过程与加密过程采用相同的算法：密文分组。

按下述规则计算，1≤i≤n，轮函数为F

$LD_i = RD_{i-1}$

$RD_i = LD_{i-1}\bigoplus F(RD_{i-1},K_{n-i+1})$

进行n轮迭代运算后，得，输出明文

下面即需要证明 ，显然：

$LD_i = RD_{i-1} = LE_{n+1-i} = RE_{n-i}$

$RD_i=LD_{i-1} \bigoplus F(RD_{i-1},K_{n+1-i}) = RE_{n+1-i}\bigoplus F(LE_{n+1-i},K_{n+1-i}) = LE_{n-i}$

当i=0可得，所以Feistel结构是可逆的。

课后习题

根据对明文处理方式的不同，对称加密可以分为哪两种？

流密码和分组密码。

DES算法中IP置换的作用？

IP置换其作用是通过将明文的每个比特位移到不同的位置上，实现对明文的置换和重排。这个过程实际上是扩散,让明文中的每一位影响密文中的许多位

DES算法中16轮迭代运算的作用？

增强密码算法的安全性,由于DES算法的密钥长度较短，因此进行多轮迭代能够增强算法的复杂度和安全性，使其更难被攻击者破解;实现分组加密：DES算法采用了分组加密的方式，将明文数据分成左右两个部分并进行迭代加密，这种方式既方便了数据的处理，又增强了算法的安全性。

本质上讲，数据的保密性是密钥的保密性还是算法的保密性？

当然是密钥的保密性！

双钥加密体制

怎么说

没找着公钥加密在哪，所以就接着写了。

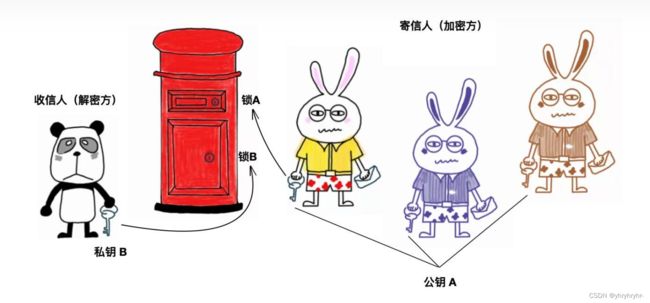
公钥加密，也叫非对称（密钥）加密，属于通信科技下的网络安全二级学科，指的是由对应的一对唯一性密钥（即公开密钥和私有密钥）组成的加密方法。它解决了密钥的发布和管理问题，是商业密码的核心。在公钥加密体制中，没有公开的是私钥，公开的是公钥。

下面，三只和一只将为您展示公钥加密过程。如下图所示。

非对称加、解密过程：

消息接收方准备好公钥和私钥
私钥接收方自己留存、公钥发布给消息发送方
消息发送方使用接收方公钥对消息进行加密
消息接收方用自己的私钥对消息解密

欧几里得算法求逆

算数

例题，求17在模26下的逆元。 $17x \equiv 1 \mod 26$

$26 \equiv 1 \times 17+9,17 \equiv 9+8,9=8 \times 1+1$

$1 \equiv 9-8 \equiv 2\times9-17 \equiv 2\times 26 -3 \times 17$

$\therefore 17^{-1} \mod 26 \equiv -3 \equiv 23 \mod 26$

算式

求在 $\mod x^8+x^4+x^3+x+1$ 下的逆元

首先需要证明和 $\mod x^8+x^4+x^3+x+1$ 的最大公约数为1，否则不存在这个逆元。

倒推下来：

$-x = x^2-x(x+1),\therefore 1=(1-x)(1+x)+x^2$

$\therefore 1=(1-x)[x^8+x^4+x^3+x+1-(x^6+x^2+x)x^2]+x^2$

$\therefore x^2$ 在 $\mod x^8+x^4+x^3+x+1$ 下的逆元为

RSA算法

加解密过程

选择一对不相等的大质数，记作p、q
计算 $N = p \times q$
计算 $\phi(N) = (p-1)\times(q-1)$
选择一个与 $\phi(N)$ 互质的整数e
计算出e对于φ(N)的模反元素d
公钥 KU = (e,N) ，私钥KR = (d,N) 注意这括号不是最大公约数，而是表达形式，具体见例题！

如果两个正整数e和φ(n)互质，那么⼀定可以找到⼀个整数d，使得ed-1被φ(n)整除，或者说ed除以φ(n)所得余数为1。此时，d就叫做e的模反元素。

加密 $M^e \mod N \equiv C$

解密 $C^d \mod N \equiv M$

例题

取p=3、q=11;
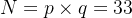
$N=p \times q = 33$
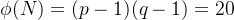
$\phi(N) = (p-1)(q-1) = 20$
选择一个与\phi(N)互素的数，我们选择e=3
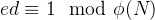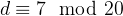
找到一个d使得 $ed \equiv 1 \mod \phi(N)$ ，解得 $d \equiv 7 \mod 20$
公钥KU = (e,n) = (3,33) ，私钥KR = (d,n) = (7,33)

假如明文M=20，加密即为 $20^3 \mod 33 = 14$ ，解密即为 $14^7 \mod 33 = 20$

椭圆曲线加密

推导出生成秘钥k和加法公式，已知 $y^2 = x^3+ax+b \mod P$

注意，公式中不论P、Q两点是不是横坐标相同，只区分两点是否重合。

例题_基础

利用椭圆曲线实现ElGamal密码体制，设椭圆曲线是 $E_{11}(1,6)$ ，生成元 G=(2,7)

求

已知椭圆曲线方程为 $y^2 = x^3+x+6 \mod 11$

$k\equiv\frac{7-2}{2-5}\mod 11\equiv5\times(-3)^{-1}\equiv5\times7 \mod 11 \equiv 2 \mod 11$

$x_3 \equiv k^2-x_1-x_2\equiv2^2-5-2 \equiv 8\mod 11$

$y_3 \equiv 2\times(5-8)-2 \mod 11\equiv 3 \mod 11$

所以

例题_复杂

Diffie- Hellman 密钥交换算法

基本原理

例题

设a=3,q=17

Alice: X_A = 15；Bob: X_B = 13

$Y_A = 3^{15} \mod 17 \equiv6$ ； $Y_B = 3^{13} \mod 17 \equiv 12$

把6传给Bob；把12传给Alice

$12^{15} \mod 17 \equiv 10 6^{13} \mod 17 \equiv 10$ 这样他们就有了共同的密钥“10”s

如上图，Alice和Bob以为自己和对方交换了秘钥，但实质上都是和Darth交换秘钥，所以Darth可以获得Alice和Bob的所有明文，这样就寄了！

ElGamal签名机制

加解密过程

已知p是大素数，g是 $Z_p^{*}$ 的本原根，x为用户私钥， $y \equiv g^x \mod p$ 为公钥，选择随机数 $k\in Z_p^{*}$ 。m为签名的消息。

计算Hash(m)。

计算 $r=g^k \mod p$

计算 $s=[Hash(m)-x*r]k^{-1} \mod (p-1)$

签名即将消息m，(r,s)送给对方。

验证时需要计算：

$y^rr^s \equiv g^{xr}g^{sk} \mod p \equiv g^{xr+sk} \mod p$

而计算s时不难看出， $xr+sk \equiv Hash(m) \mod (p-1)$

所以拿到m后，先计算 $g^{Hash(m)} \mod p$ ，再计算 $y^rr^s \mod p$ ，如果两者相等则消息m被发送者用私钥x签名过。

例题

，对消息m进行签名

$r \equiv g^k \mod p \equiv 8 \mod 29$

$s \equiv [Hash(m)-x*r]k^{-1} \mod (p-1) \equiv [19-2*8]3^{-1} \mod 28 \equiv 1$

发送消息m和数字签名(r,s)

验证计算 $g^{Hash(m)} \equiv 2^{19} \mod 29$ ，

$y^rr^s \equiv 4^8*8 \mod p \equiv 2^{19} \mod29$ ，签名验证正确。

Schnorr签名机制

p、q为选取的大素数，g 满足 $g^q \equiv 1 \mod p$ ，x为私钥， $y \equiv g^x \mod p$ 为公钥。

计算 $r \equiv g^k \mod p$

计算

计算 $s \equiv k+xe \mod q$

数字签名为(e,s)，将m和数字签名发送给检验方。

检验时计算 $r^{'} \equiv g^sy^{-e} \mod p$ ，再计算 $Hash(r^{'}||m)$ ，如果结果为e则签名有效。

DSS签名算法——DSA

先前条件和之前相同。

计算 $r \equiv (g^k \mod p) \mod q$

计算 $s \equiv [k^{-1}(Hash(m)+xr)] \mod q$

数字签名为(r,s)，将消息m和签名(r,s)发给检测方。

收到m后计算Hash(m)，再计算 $w \equiv s^{-1} \mod q$

计算 $u_1 \equiv [Hash(m)*w] \mod q$ ， $u_2 \equiv r*w \mod q$

$v \equiv [(g^{u_1}y^{u_2}) \mod p] \mod q$ ，如果 $v \equiv r$ 则签名有效。

基于社交网络算法优化的二维最大熵图像分割智能算法研学社（Jack旭）智能优化算法应用图像分割算法 php 开发语言
智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
2023-04-17|篮球女孩长一木
1小学抑或初中阶段，在课外书了解到她的故事。“篮球女孩”。当时佩服她的顽强，也对生命多了一丝敬畏。今天刚好在公众号看到，长大后的“篮球女孩”。佩服之余又满是心疼。网络侵删祝那素未蒙面的女孩，未来一切顺遂。
在一台Ubuntu计算机上构建Hyperledger Fabric网络落叶无声9 区块链超级账本 Hyperledger fabric 区块链 ubuntu 构建 hyperledger fabric
在一台Ubuntu计算机上构建HyperledgerFabric网络Hyperledgerfabric是一个开源的区块链应用程序平台，为开发基于区块链的应用程序提供了一个起点。当我们提到HyperledgerFabric网络时，我们指的是使用HyperledgerFabric的正在运行的系统。即使只使用最少数量的组件，部署Fabric网络也不是一件容易的事。Fabric社区创建了一个名为Cello
【华为OD技术面试真题 - 技术面】-测试八股文真题题库（1）算法大师华为od 面试 python 算法前端
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.黑盒测试和白盒测试的区别2.假设我们公司现在开发一个类似于微信的软件1.0版本，现在要你测试这个功能：打开聊天窗口，输入文本，限制字数在200字以内。问你怎么提取测试点。功能测试性能测试安全性测试可用性测试跨平台兼容性测试网络环境测试3.接口测试的工具你了解哪些
Low Power概念介绍-Voltage Area 飞奔的大虎
随着智能手机，以及物联网的普及，芯片功耗的问题最近几年得到了越来越多的重视。为了实现集成电路的低功耗设计目标，我们需要在系统设计阶段就采用低功耗设计的方案。而且，随着设计流程的逐步推进，到了芯片后端设计阶段，降低芯片功耗的方法已经很少了，节省的功耗百分比也不断下降。芯片的功耗主要由静态功耗（staticleakagepower）和动态功耗(dynamicpower)构成。静态功耗主要是指电路处于等
《在战“疫”中成长致敬生活》观后感梅子刘的刀
（作者：周晨）今天上午，我看了“我是接班人”网络大课堂《在战役中成长致敬生活》。有很多人拿出自己攒下的钱，默默地捐给了武汉，有几千块钱的、有几万块钱的，也有十几万块钱的。连小朋友也把自己的压岁钱捐给了武汉。有名环卫工人把自己五年的积蓄全部捐给了武汉。有名外卖小哥为医护人员买鞋子送吃的。还有已经治愈出院的新型肺炎病人捐了400毫升的血浆。还有位叫大树的叔叔，虽然他没有钱，但是他地里有蔬菜，捐了几大卡
数字里的世界17期：2021年全球10大顶级数据中心，中国移动榜首张三叨
你知道吗？2016年，全球的数据中心共计用电4160亿千瓦时，比整个英国的发电量还多40％！前言每天，我们都会创造超过250万TB的数据。并且随着物联网（IOT）的不断普及，这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代，但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术，比如人工智能和机器学习，已经将我们推向
中原焦点团队网络初中级30期阴丽丽坚持分享第三百八十八次2022.10.18分享约练次数（74）咨询师（6）来访者（53）观察者（15）阴丽丽
今天是忙碌的一天，一早起来，总想着找点把事情弄完，可总也弄不完。就这样弄着吧！孩子的事，自己的事都在那里搁置着，不想做，有点欧！今天总体还不错，只是在下午起床时走神了俩小时，也算是给自己的放松吧！今日难得1.儿子乖巧、听话，努力配合，一天下来也是忙忙碌碌，这真的很难得！2.儿子今天录的视频被班主任认可，这真的很难得3.我今天早上做核酸时，自己把教案整了一下，这真的很难得
网络编程基础记得开心一点啊网络
目录♫什么是网络编程♫Socket套接字♪什么是Socket套接字♪数据报套接字♪流套接字♫数据报套接字通信模型♪数据报套接字通讯模型♪DatagramSocket♪DatagramPacket♪实现UDP的服务端代码♪实现UDP的客户端代码♫流套接字通信模型♪流套接字通讯模型♪ServerSocket♪Socket♪实现TCP的服务端代码♪实现TCP的客户端代码♫什么是网络编程网络编程，指网络上
多子女家庭问题 3e5c5362403c
杨宁宁焦点解决网络初17中19坚持分享589天（2021.3.20）本周约练我1次，总计166次，读书打卡第256天案例督导收获：【家有老大篇】被爱与高期待下的独舞家里的第一个孩子往往集万千宠爱于一身。爸爸妈妈、爷爷奶奶、姥姥姥爷的目光都聚焦在他的身上。在这种光环下长大的孩子，就如小皇帝一般，衣来伸手、饭来张口。拥有爱的同时，也意味着拥有了更高的被期待，父母会花血本给你报各种各样的早教班，给你买各
父母教育孩子的方式，将影响孩子一生树英教育
为什么有些孩子总是充满自信与快乐？独立、有主见又坚强？而有些孩子却自卑、胆怯，软弱又过度依赖父母？为什么有些孩子总是健康、阳光又富于创造力？而有些孩子却悲观、孤僻又思想空乏？一个孩子的行为取决于孩子的思想，思想取决于环境和自己的认知，认知取决于教育。父母是孩子人生中的第一位教育者，父母养育孩子的方式，将决定他们人生的高度，影响他们的一生。网络图，侵权即删优秀的父母就像园丁，既要浇水施肥，又要修剪杂
2024.9.6 Python，华为笔试题总结，字符串格式化，字符串操作，广度优先搜索解决公司组织绩效互评问题，无向图 RaidenQ python 华为 leetcode 算法力扣广度优先无向图
1.字符串格式化name="Alice"age=30formatted_string="Name:{},Age:{}".format(name,age)print(formatted_string)或者name="Alice"age=30formatted_string=f"Name:{name},Age:{age}"print(formatted_string)2.网络健康检查第一行有两个整数m
戴容容中原焦点团队.网络初级第33期,坚持分享第19天 2022年3月9日 TessDai
《每个人眼中的世界都是不同的》“一千个人眼里有一千个哈姆雷特”世界是多元的,每个人都有自己的道理,人人按照自己的理解去看待这个世界的人和物.我们如此,其他人也是如此.因此,任何事情,我们要放下自己以为的真理,去理解他人认为的真理,只有同频方能共振.孩子在慢慢长大的过程中慢慢学会独立,甚至对抗.尤其当孩子处于青春期的时候,他们开始有很多自己独立的想法,和一些特立独行的做法,家长常常会觉得不可思议,觉
第1步win10宿主机与虚拟机通过NAT共享上网互通学习3人组大数据大数据
VM的CentOS采用NAT共用宿主机网卡宿主机器无法连接到虚拟CentOS要实现宿主机与虚拟机通信，原理就是给宿主机的网卡配置一个与虚拟机网关相同网段的IP地址，实现可以互通。1、查看虚拟机的IP地址2、编辑虚拟机的虚拟网络的NAT和DHCP的配置，设置虚拟机的网卡选择NAT共享模式3、宿主机的IP配置，确保vnet8的IPV4属性与虚拟机在同一网段4、ping测试连通性[root@localh
网络通信流程记得开心一点啊服务器网络运维
目录♫IP地址♫子网掩码♫MAC地址♫相关设备♫ARP寻址♫网络通信流程♫IP地址我们已经知道IP地址由网络号+主机号组成，根据IP地址的不同可以有5钟划分网络号和主机号的方案：其中，各类地址的表示范围是：分类范围适用网络网络数量主机最大连接数A类0.0.0.0~127.255.255.255大型网络12616777214【(2^24)-2】B类128.0.0.0~191.255.255.255中
Java爬虫框架（一）--架构设计狼图腾-狼之传说 java 框架 java 任务 html解析器存储电子商务
一、架构图那里搜网络爬虫框架主要针对电子商务网站进行数据爬取，分析，存储，索引。爬虫：爬虫负责爬取，解析，处理电子商务网站的网页的内容数据库：存储商品信息索引：商品的全文搜索索引Task队列：需要爬取的网页列表Visited表：已经爬取过的网页列表爬虫监控平台：web平台可以启动，停止爬虫，管理爬虫，task队列，visited表。二、爬虫1.流程1)Scheduler启动爬虫器，TaskMast
计算机木马详细编写思路小熊同学哦 php 开发语言木马木马思路
导语：计算机木马（ComputerTrojan）是一种恶意软件，通过欺骗用户从而获取系统控制权限，给黑客打开系统后门的一种手段。虽然木马的存在给用户和系统带来严重的安全风险，但是了解它的工作原理与编写思路，对于我们提高防范意识、构建更健壮的网络安全体系具有重要意义。本篇博客将深入剖析计算机木马的详细编写思路，以及如何复杂化挑战，以期提高读者对计算机木马的认识和对抗能力。计算机木马的基本原理计算机木
Mongodb Error: queryTxt ETIMEOUT xxxx.wwwdz.mongodb.net 佛一脚 error react mongodb 数据库
背景每天都能遇到奇怪的问题，做个记录，以便有缘人能得到帮助！换了一台电脑开发nextjs程序。需要连接mongodb数据，对数据进行增删改查。上一台电脑好好的程序，新电脑死活连不上mongodb数据库。同一套代码，没任何修改，搞得我怀疑人生了，打开浏览器进入mongodb官网毫无问题，也能进入线上系统查看数据，网络应该是没问题。于是我尝试了一下手机热点，这次代码能正常跑起来，连接数据库了！！！是不
高考后该不该给孩子买电脑，什么情况能买？什么情况不能买？寻求改变
我知道家长们很担心，怕买了电脑小孩沉迷游戏，耽误了学业，也不利于身体健康。对于准大学生来说，基本上在18岁左右，也不算小了，但在很多父母眼里，依旧是个小孩子。数据显示，这种情况是有发生的，大学生约70%的电脑主要被用于玩网络游戏，如果没有养成一个用良好的习惯，对孩子影响是非常大的。我总结为三买，三不买。最近有看到群里很多家长再问，小孩上大学该不该给他买电脑，要买和不买两种观点的家长都有，那么哪种情
ESP32-C3入门教程网络篇⑩——基于esp_https_ota和MQTT实现开机主动升级和被动触发升级的OTA功能小康师兄 ESP32-C3入门教程 https 服务器 esp32 OTA MQTT
文章目录一、前言二、软件流程三、部分源码四、运行演示一、前言本文基于VSCodeIDE进行编程、编译、下载、运行等操作基础入门章节请查阅：ESP32-C3入门教程基础篇①——基于VSCode构建HelloWorld教程目录大纲请查阅：ESP32-C3入门教程——导读ESP32-C3入门教程网络篇⑨——基于esp_https_ota实现史上最简单的ESP32OTA远程固件升级功能二、软件流程
中国广电永久9元流量套餐！性价比最高流量卡套餐介绍！优惠攻略官
中国广电是中国最大的传媒集团之一，其推出的流量套餐备受消费者青睐。中国广电最实惠的流量套餐不仅价格亲民，而且提供了优质的网络体验。首先，中国广电的流量套餐价格实惠，适合不同消费者的需求。无论是短期的日租卡还是长期有效的月租卡，用户都可以根据自己的实际情况选择适合自己的套餐。而且，流量的价格相对于其他运营商的套餐来说更加合理，给用户提供了更大的选择空间。☞大流量卡套餐「→点这免费申请办理」或者截图扫
WebMagic：强大的Java爬虫框架解析与实战 Aaron_945 Java java 爬虫开发语言
文章目录引言官网链接WebMagic原理概述基础使用1.添加依赖2.编写PageProcessor高级使用1.自定义Pipeline2.分布式抓取优点结论引言在大数据时代，网络爬虫作为数据收集的重要工具，扮演着不可或缺的角色。Java作为一门广泛使用的编程语言，在爬虫开发领域也有其独特的优势。WebMagic是一个开源的Java爬虫框架，它提供了简单灵活的API，支持多线程、分布式抓取，以及丰富的
4 大低成本娱乐方式: 小说, 音乐, 视频, 电子游戏穷人小水滴娱乐音视频低成本小说游戏
穷人如何获得快乐?小说,音乐,视频,游戏,本文简单盘点一下这4大低成本(安全)娱乐方式.这里是穷人小水滴,专注于穷人友好型低成本技术.(本文为58号作品.)目录1娱乐方式1.1小说(网络小说)1.2音乐1.3视频(b站)1.4游戏(电子游戏/计算机软件)2低成本:一只手机即可3总结与展望1娱乐方式这几种,也可以说是艺术的具体形式.更专业的说,(娱乐)是劳动力再生产的重要组成部分.使人放松,获得快乐
00. 这里整理了最全的爬虫框架（Java + Python）有一只柴犬爬虫系列爬虫 java python
目录1、前言2、什么是网络爬虫3、常见的爬虫框架3.1、java框架3.1.1、WebMagic3.1.2、Jsoup3.1.3、HttpClient3.1.4、Crawler4j3.1.5、HtmlUnit3.1.6、Selenium3.2、Python框架3.2.1、Scrapy3.2.2、BeautifulSoup+Requests3.2.3、Selenium3.2.4、PyQuery3.2
计算机网络八股总结 Petrichorzncu 八股总结计算机网络笔记
这里写目录标题网络模型划分（五层和七层）及每一层的功能五层网络模型七层网络模型（OSI模型）==三次握手和四次挥手具体过程及原因==三次握手四次挥手TCP/IP协议组成==UDP协议与TCP/IP协议的区别==Http协议相关知识网络地址，子网掩码等相关计算网络模型划分（五层和七层）及每一层的功能五层网络模型应用层：负责处理网络应用程序，如电子邮件、文件传输和网页浏览。主要协议包括HTTP、FTP
每日头像|爱与时光，终年不遇一宝先生
小可爱们晚上好呀今天晚上来推送一期情侣头像~喜欢的小可爱可以点赞收藏评论哟~部分素材来自网络，版权归原创者，如有侵权请联系删除今天的头像结束啦喜欢的小可爱可以点下关注哟~如果喜欢本期的内容可以转发分享哦~那我们下期再见咯~拜了个拜~
深入浅出 -- 系统架构之负载均衡Nginx的性能优化 xiaoli8748_软件开发系统架构系统架构负载均衡 nginx
一、Nginx性能优化到这里文章的篇幅较长了，最后再来聊一下关于Nginx的性能优化，主要就简单说说收益最高的几个优化项，在这块就不再展开叙述了，毕竟影响性能都有多方面原因导致的，比如网络、服务器硬件、操作系统、后端服务、程序自身、数据库服务等，对于性能调优比较感兴趣的可以参考之前《JVM性能调优》中的调优思想。优化一：打开长连接配置通常Nginx作为代理服务，负责分发客户端的请求，那么建议开启H
进销存小程序源码 PHP网络版ERP进销存管理系统全开源可二开摸鱼小号 php
可直接源码搭建部署发布后使用：一、功能模块介绍该系统模板主要有进，销，存三个主要模板功能组成，下面将介绍各模块所对应的功能；进：需要将产品采购入库，自动生成采购明细台账同时关联财务生成付款账单；销：是指对客户的销售订单记录，汇总生成产品销售明细及回款计划；存：库存的日常盘点与统计，库存下限预警、出入库台账、库存位置等。1.进购管理采购订单：采购下单审批→由上级审批通过采购入库；采购入库：货品到货>
年的味道~ 心理疗愈师英子
小时候，最期盼过年，一想到过年有压岁钱拿、有新衣服穿、不用上学还有好东西吃，就兴奋不已。可是不知道从什么时候开始，很多人那种儿时满怀期待过年的感觉没有了，对年的期盼也越来越少。现在物质极大丰富，以前过年才有的丰盛年夜饭，现在几乎已成家常便饭，对过年有好东西吃的期盼没了。现在网络购物发达，服装店也遍布大街小巷，随时都可以添置新衣服，而不必非要等到过年，儿时那种大年初一从头新到脚的仪式感没有了。放鞭炮
2021-07-09 2018心如止水
张雲芳焦点解决网络课程学习坚持分享第816天20210709本周第2次（约练总291）渴了喝水；饿了吃饭；累了休息。看似简单的选择与行为，做起来却没那么容易。尤其是作为成年人，每天有工作需要完成，有孩子、家人需要陪伴，有时候各种事情赶在一起，忙的晕头转向、焦头烂额，即使自己特别累，也没有间隙去休息一下下，想象一下身体疲惫，精力耗竭是什么样的状态？对于孩子的哭闹你还会有更多的耐心吗？我想多数情况下都
多线程编程之join()方法周凡杨 java JOIN 多线程编程线程
现实生活中，有些工作是需要团队中成员依次完成的，这就涉及到了一个顺序问题。现在有T1、T2、T3三个工人，如何保证T2在T1执行完后执行，T3在T2执行完后执行？问题分析：首先问题中有三个实体，T1、T2、T3，因为是多线程编程，所以都要设计成线程类。关键是怎么保证线程能依次执行完呢？ Java实现过程如下： public class T1 implements Runnabl
java中switch的使用 bingyingao java enum break continue
java中的switch仅支持case条件仅支持int、enum两种类型。用enum的时候，不能直接写下列形式。 switch (timeType) { case ProdtransTimeTypeEnum.DAILY: break; default: br
hive having count 不能去重 daizj hive 去重 having count 计数
hive在使用having count()是，不支持去重计数 hive (default)> select imei from t_test_phonenum where ds=20150701 group by imei having count(distinct phone_num)>1 limit 10; FAILED: SemanticExcep
WebSphere对JSP的缓存周凡杨 WAS JSP 缓存
对于线网上的工程，更新JSP到WebSphere后，有时会出现修改的jsp没有起作用，特别是改变了某jsp的样式后，在页面中没看到效果，这主要就是由于websphere中缓存的缘故，这就要清除WebSphere中jsp缓存。要清除WebSphere中JSP的缓存，就要找到WAS安装后的根目录。现服务
设计模式总结朱辉辉33 java 设计模式
1.工厂模式 1.1 工厂方法模式 (由一个工厂类管理构造方法) 1.1.1普通工厂模式(一个工厂类中只有一个方法) 1.1.2多工厂模式(一个工厂类中有多个方法) 1.1.3静态工厂模式(将工厂类中的方法变成静态方法) &n
实例：供应商管理报表需求调研报告老A不折腾 finereport 报表系统报表软件信息化选型
引言随着企业集团的生产规模扩张，为支撑全球供应链管理，对于供应商的管理和采购过程的监控已经不局限于简单的交付以及价格的管理，目前采购及供应商管理各个环节的操作分别在不同的系统下进行，而各个数据源都独立存在，无法提供统一的数据支持；因此，为了实现对于数据分析以提供采购决策，建立报表体系成为必须。业务目标 1、通过报表为采购决策提供数据分析与支撑 2、对供应商进行综合评估以及管理，合理管理和
mysql 林鹤霄
转载源：http://blog.sina.com.cn/s/blog_4f925fc30100rx5l.html mysql -uroot -p ERROR 1045 (28000): Access denied for user 'root'@'localhost' (using password: YES) [root@centos var]# service mysql
Linux下多线程堆栈查看工具(pstree、ps、pstack) aigo linux
原文：http://blog.csdn.net/yfkiss/article/details/6729364 1. pstree pstree以树结构显示进程$ pstree -p work | grep adsshd(22669)---bash(22670)---ad_preprocess(4551)-+-{ad_preprocess}(4552) &n
html input与textarea 值改变事件 alxw4616 JavaScript
// 文本输入框(input) 文本域(textarea)值改变事件 // onpropertychange(IE) oninput(w3c) $('input,textarea').on('propertychange input', function(event) { console.log($(this).val()) });
String类的基本用法百合不是茶 String
字符串的用法; // 根据字节数组创建字符串 byte[] by = { 'a', 'b', 'c', 'd' }; String newByteString = new String(by); 1,length() 获取字符串的长度 &nbs
JDK1.5 Semaphore实例 bijian1013 java thread java多线程 Semaphore
Semaphore类一个计数信号量。从概念上讲，信号量维护了一个许可集合。如有必要，在许可可用前会阻塞每一个 acquire()，然后再获取该许可。每个 release() 添加一个许可，从而可能释放一个正在阻塞的获取者。但是，不使用实际的许可对象，Semaphore 只对可用许可的号码进行计数，并采取相应的行动。 S
使用GZip来压缩传输量 bijian1013 java GZip
启动GZip压缩要用到一个开源的Filter：PJL Compressing Filter。这个Filter自1.5.0开始该工程开始构建于JDK5.0，因此在JDK1.4环境下只能使用1.4.6。 PJL Compressi
【Java范型三】Java范型详解之范型类型通配符 bit1129 java
定义如下一个简单的范型类， package com.tom.lang.generics; public class Generics<T> { private T value; public Generics(T value) { this.value = value; } }
【Hadoop十二】HDFS常用命令 bit1129 hadoop
1. 修改日志文件查看器 hdfs oev -i edits_0000000000000000081-0000000000000000089 -o edits.xml cat edits.xml 修改日志文件转储为xml格式的edits.xml文件，其中每条RECORD就是一个操作事务日志 2. fsimage查看HDFS中的块信息等 &nb
怎样区别nginx中rewrite时break和last ronin47
在使用nginx配置rewrite中经常会遇到有的地方用last并不能工作，换成break就可以，其中的原理是对于根目录的理解有所区别，按我的测试结果大致是这样的。 location / { proxy_pass http://test;
java-21.中兴面试题输入两个整数 n 和 m ，从数列 1 ， 2 ， 3.......n 中随意取几个数 , 使其和等于 m bylijinnan java
import java.util.ArrayList; import java.util.List; import java.util.Stack; public class CombinationToSum { /* 第21 题 2010 年中兴面试题编程求解：输入两个整数 n 和 m ，从数列 1 ， 2 ， 3.......n 中随意取几个数 , 使其和等
eclipse svn 帐号密码修改问题开窍的石头 eclipse SVN svn帐号密码修改
问题描述： Eclipse的SVN插件Subclipse做得很好，在svn操作方面提供了很强大丰富的功能。但到目前为止，该插件对svn用户的概念极为淡薄，不但不能方便地切换用户，而且一旦用户的帐号、密码保存之后，就无法再变更了。解决思路：删除subclipse记录的帐号、密码信息，重新输入
[电子商务]传统商务活动与互联网的结合 comsci 电子商务
某一个传统名牌产品，过去销售的地点就在某些特定的地区和阶层，现在进入互联网之后，用户的数量群突然扩大了无数倍，但是，这种产品潜在的劣势也被放大了无数倍，这种销售利润与经营风险同步放大的效应，在最近几年将会频繁出现。。。。如何避免销售量和利润率增加的
java 解析 properties-使用 Properties-可以指定配置文件路径 cuityang java properties
#mq xdr.mq.url=tcp://192.168.100.15:61618; import java.io.IOException; import java.util.Properties; public class Test { String conf = "log4j.properties"; private static final
Java核心问题集锦 darrenzhu java 基础核心难点
注意，这里的参考文章基本来自Effective Java和jdk源码 1)ConcurrentModificationException 当你用for each遍历一个list时，如果你在循环主体代码中修改list中的元素，将会得到这个Exception，解决的办法是： 1)用listIterator, 它支持在遍历的过程中修改元素， 2)不用listIterator, new一个
1分钟学会Markdown语法 dcj3sjt126com markdown
markdown 简明语法基本符号 *,-,+ 3个符号效果都一样，这3个符号被称为 Markdown符号空白行表示另起一个段落 `是表示inline代码，tab是用来标记代码段，分别对应html的code，pre标签换行单一段落( <p>) 用一个空白行连续两个空格会变成一个 <br> 连续3个符号，然后是空行
Gson使用二（GsonBuilder） eksliang json gson GsonBuilder
转载请出自出处：http://eksliang.iteye.com/blog/2175473 一.概述 GsonBuilder用来定制java跟json之间的转换格式二.基本使用实体测试类：温馨提示：默认情况下@Expose注解是不起作用的,除非你用GsonBuilder创建Gson的时候调用了GsonBuilder.excludeField
报ClassNotFoundException: Didn't find class "...Activity" on path: DexPathList gundumw100 android
有一个工程，本来运行是正常的，我想把它移植到另一台PC上，结果报： java.lang.RuntimeException: Unable to instantiate activity ComponentInfo{com.mobovip.bgr/com.mobovip.bgr.MainActivity}: java.lang.ClassNotFoundException: Didn't f
JavaWeb之JSP指令 ihuning javaweb
要点 JSP指令简介 page指令 include指令 JSP指令简介 JSP指令（directive）是为JSP引擎而设计的，它们并不直接产生任何可见输出，而只是告诉引擎如何处理JSP页面中的其余部分。 JSP指令的基本语法格式： <%@ 指令属性名="
mac上编译FFmpeg跑ios 啸笑天 ffmpeg
1、下载文件：https://github.com/libav/gas-preprocessor，复制gas-preprocessor.pl到/usr/local/bin/下，修改文件权限：chmod 777 /usr/local/bin/gas-preprocessor.pl 2、安装yasm-1.2.0 curl http://www.tortall.net/projects/yasm
sql mysql oracle中字符串连接 macroli oracle sql mysql SQL Server
有的时候，我们有需要将由不同栏位获得的资料串连在一起。每一种资料库都有提供方法来达到这个目的： MySQL: CONCAT() Oracle: CONCAT(), || SQL Server: + CONCAT() 的语法如下： Mysql 中 CONCAT(字串1, 字串2, 字串3, ...): 将字串1、字串2、字串3，等字串连在一起。请注意，Oracle的CON
Git fatal: unab SSL certificate problem: unable to get local issuer ce rtificate qiaolevip 学习永无止境每天进步一点点 git 纵观千象
// 报错如下： $ git pull origin master fatal: unable to access 'https://git.xxx.com/': SSL certificate problem: unable to get local issuer ce rtificate // 原因：由于git最新版默认使用ssl安全验证，但是我们是使用的git未设
windows命令行设置wifi surfingll windows wifi 笔记本wifi
还没有讨厌无线wifi的无尽广告么，还在耐心等待它慢慢启动么教你命令行设置笔记本电脑wifi： 1、开启wifi命令 netsh wlan set hostednetwork mode=allow ssid=surf8 key=bb123456 netsh wlan start hostednetwork pause 其中pause是等待输入，可以去掉 2、
Linux（Ubuntu）下安装sysv-rc-conf wmlJava linux ubuntu sysv-rc-conf
安装：sudo apt-get install sysv-rc-conf 使用：sudo sysv-rc-conf 操作界面十分简洁，你可以用鼠标点击，也可以用键盘方向键定位，用空格键选择，用Ctrl+N翻下一页，用Ctrl+P翻上一页，用Q退出。背景知识 sysv-rc-conf是一个强大的服务管理程序，群众的意见是sysv-rc-conf比chkconf
svn切换环境，重发布应用多了javaee标签前缀 zengshaotao javaee
更换了开发环境，从杭州，改变到了上海。svn的地址肯定要切换的，切换之前需要将原svn自带的.svn文件信息删除，可手动删除，也可通过废弃原来的svn位置提示删除.svn时删除。然后就是按照最新的svn地址和规范建立相关的目录信息，再将原来的纯代码信息上传到新的环境。然后再重新检出，这样每次修改后就可以看到哪些文件被修改过，这对于增量发布的规范特别有用。检出

网络安全复习

低层协议安全性

IP协议

ARP协议

TCP协议

NAT协议

单钥加密体制

DES算法

课后习题

双钥加密体制

怎么说

欧几里得算法求逆

RSA算法

椭圆曲线加密

Diffie- Hellman 密钥交换算法

ElGamal签名机制

Schnorr签名机制

DSS签名算法——DSA

你可能感兴趣的:(网络安全,网络协议,网络,物联网)