树的概念和性质
文章目录
- 树的基本概念
-
- 树的定义和术语
- 树的遍历
- 树的种类
- 二叉树
-
- 二叉搜索树
-
- AVL 树
- 红黑树
- 完全二叉树和满二叉树
- 哈夫曼树
- 多叉树
- B 树及其变种
-
- B 树
- B+ 树和 B* 树
- 目录
树的基本概念
树的定义和术语
树是由零个或多个结点组成的具有层级关系的数据结构。
当树的结点数量等于零时,称为空树。当树的结点数量大于零时,定义以下术语:根结点、叶结点、父结点、子结点、子树。
- 树中有一个唯一的根结点。
- 每个结点有零个或多个子结点,没有子结点的结点称为叶结点。
- 根结点没有父结点,除了根结点以外的每个结点有且只有一个父结点。
- 父结点和子结点是相对关系,甲结点是乙结点的父结点等价于乙结点是甲结点的子结点。
- 对于父结点而言,以子结点为根结点的树称为父结点的子树。
根据父结点和子结点的定义,还可以定义兄弟结点、堂兄弟结点、祖先和后代。
- 如果两个结点的父结点相同,则这两个结点为兄弟结点。
- 如果两个结点的父结点不同且位于同一层,则这两个结点为堂兄弟结点。
- 如果以结点甲为根的子树中存在结点乙,则结点甲是结点乙的祖先,结点乙是结点甲的后代。
由于树中的结点之间存在层级关系,因此还需要定义树中的边、结点的层级以及树的层级和树的高度。层级和高度的定义取决于具体场景。
- 当且仅当两个结点之间的关系是父结点和子结点的关系时,两个结点之间有一条边相连。
- 根结点所在层定义为第 0 0 0 层或第 1 1 1 层。如果两个结点之间的关系是父结点和子结点的关系,则子结点的层数为父结点的层数加 1 1 1。
- 树的层级定义为树中结点所在的不同层级的数量,为最远叶结点的层数和根结点的层数之差加 1 1 1。
- 树的高度可以定义为:树的层级;从根结点到最远叶结点的路径上的边数;从根结点到最远叶结点的路径上的结点数。
由于树中的每一条边一定连接父结点和子结点,因此树中不存在环。在树中任选两个结点,这两个结点之间的路径一定是唯一的。
树的遍历
树的遍历指的是按照特定顺序依次访问树中的每个结点,使得每个结点恰好被访问一次。树的遍历可以分成两大类,基于深度优先搜索的遍历和基于广度优先搜索的遍历。
深度优先搜索的方法为:从根结点开始,对于每个可能的分支路径深入搜索下一个结点,遇到叶结点时,回退到上一个结点并对其余的分支路径继续搜索,直到遍历完所有可能的分支路径。深度优先搜索基于栈实现,可以通过递归的方式或者显性使用栈的方式实现。
广度优先搜索的方法为:从根结点开始,依次遍历每一层的结点,直到遍历完最后一层的结点。广度优先搜索基于队列实现。
二叉树和多叉树部分将会具体介绍树的遍历方法。
树的种类
树的种类有很多,以下列举常见的树。
- 二叉树:最常见的树结构,树中的每个结点最多有两个子结点,两个结点分别为左子结点和右子结点。特殊的二叉树包括二叉搜索树、完全二叉树、满二叉树、哈夫曼树等。
- 多叉树:最一般化的树结构,树中的每个结点可以有任意个子结点。
- B 树:多叉树的一种,也称平衡多路搜索树,适用于磁盘和其他存储设备。B 树的两个常见的变种是 B+ 树和 B* 树。
- 字典树:也称前缀树,为多叉树的一种,可以用于字符串的检索,其使用空间小于哈希表。字典树将在高级数据结构部分具体讲解。
二叉树
二叉树是最常见的树结构。二叉树中的每个结点最多有两个子结点,且子结点有左右之分。
在 LeetCode 中定义了类 TreeNode \texttt{TreeNode} TreeNode,该类定义了二叉树的一个结点。 TreeNode \texttt{TreeNode} TreeNode 类的 Java 代码定义如下:
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
二叉树的遍历有四种:前序遍历、中序遍历、后序遍历和层序遍历。其中,前序遍历、中序遍历和后序遍历基于深度优先搜索,层序遍历基于广度优先搜索。
- 前序遍历的方法为:依次遍历根结点、左子树和右子树,对于左子树和右子树使用同样的方法遍历。
- 中序遍历的方法为:依次遍历左子树、根结点和右子树,对于左子树和右子树使用同样的方法遍历。
- 后序遍历的方法为:依次遍历左子树、右子树和根结点,对于左子树和右子树使用同样的方法遍历。
- 层序遍历的方法为:从根结点开始,依次遍历每一层的结点。
前序遍历、中序遍历和后序遍历可以使用递归和迭代的方式实现,时间复杂度是 O ( n ) O(n) O(n),空间复杂度是 O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数,也可以使用莫里斯遍历实现,时间复杂度是 O ( n ) O(n) O(n),空间复杂度是 O ( 1 ) O(1) O(1)。
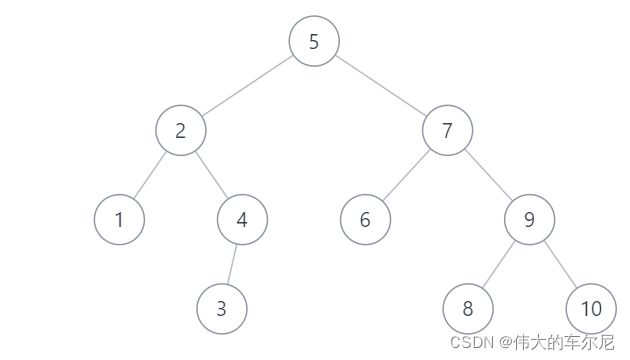
下图为一个二叉树,共有 10 10 10 个结点。
图中的二叉树的四种遍历的结果如下。
- 前序遍历: [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 ] [1,2,3,4,5,6,7,8,9,10] [1,2,3,4,5,6,7,8,9,10]。
- 中序遍历: [ 4 , 3 , 2 , 5 , 6 , 1 , 7 , 9 , 8 , 10 ] [4,3,2,5,6,1,7,9,8,10] [4,3,2,5,6,1,7,9,8,10]。
- 后序遍历: [ 4 , 3 , 6 , 5 , 2 , 9 , 10 , 8 , 7 , 1 ] [4,3,6,5,2,9,10,8,7,1] [4,3,6,5,2,9,10,8,7,1]。
- 层序遍历: [ 1 , 2 , 7 , 3 , 5 , 8 , 4 , 6 , 9 , 10 ] [1,2,7,3,5,8,4,6,9,10] [1,2,7,3,5,8,4,6,9,10]。
如果知道二叉树的前序遍历和中序遍历的结果,或者知道二叉树的中序遍历和后序遍历的结果,则可以唯一地确定二叉树。如果只知道二叉树的前序遍历和后序遍历的结果,则一般不能唯一地确定二叉树。
二叉搜索树
二叉搜索树是特殊的二叉树,结点值之间满足特定的顺序。二叉搜索树具有以下性质。
- 空二叉树(即不含任何结点的二叉树)是二叉搜索树。
- 根结点的左子树中的每一个结点的值都小于根结点的值。
- 根结点的右子树中的每一个结点的值都大于根结点的值。
- 根结点的左子树和右子树也是二叉搜索树。
下图为一个二叉搜索树。
根据二叉搜索树的性质可知,二叉搜索树的中序遍历序列中,结点值的顺序一定是递增的,因此可以根据二叉树的中序遍历序列判断二叉树是不是二叉搜索树。
利用二叉搜索树的性质,在二叉搜索树中搜索特定目标值不需要遍历全部结点,而是每次只需要在一个子树中查找,因此可以排除另一个子树中的结点。在二叉搜索树中搜索特定目标值的操作如下:从根结点开始,如果当前结点的值大于目标值则在左子树中继续搜索,如果当前结点的值小于目标值则在右子树中继续搜索,直到找到目标值,如果搜索到叶结点仍未找到目标值则目标值不存在。二叉搜索树的插入操作和删除操作都基于搜索操作,且在插入操作和删除操作之后仍然满足二叉搜索树的性质。
假设二叉搜索树的结点数是 n n n,二叉搜索树的搜索、插入和删除操作的平均时间复杂度是 O ( log n ) O(\log n) O(logn)。最坏情况下,二叉搜索树中的每个结点都只有一个子结点,此时二叉搜索树的搜索、插入和删除操作的时间复杂度退化为线性的 O ( n ) O(n) O(n)。为了避免出现二叉搜索树操作的时间复杂度过高,应将二叉搜索树维护成平衡二叉搜索树。两种常见的平衡二叉搜索树是 AVL 树和红黑树,都满足各项操作的平均时间复杂度是 O ( log n ) O(\log n) O(logn)。
AVL 树
AVL 树是平衡二叉搜索树,由两名前苏联的科学家 G. M. Adelson-Velsky 和 E. M. Landis 提出,根据两名科学家的名字命名。AVL 树具有以下性质。
- 空二叉搜索树是 AVL 树。
- 根结点的左子树和右子树的高度之差的绝对值不超过 1 1 1。
- 根结点的左子树和右子树也是 AVL 树。
下图为一个 AVL 树。
AVL 树中的每个结点都有一个平衡因子,一个结点的平衡因子定义为该结点的左子树和右子树的高度之差,AVL 树满足每个结点的平衡因子的绝对值都不超过 1 1 1。在插入和删除操作时,需要通过旋转操作维护 AVL 树的平衡性。
红黑树
红黑树是近似平衡的二叉搜索树,具有以下性质。
- 每个结点是黑色或红色。
- 根结点是黑色。
- 所有的叶结点都是黑色,红黑树中的叶结点为空结点。
- 每个红色结点的子结点都是黑色。
- 从任意一个结点出发,到其子树中的每个叶结点的所有路径都包含相同数目的黑色结点。
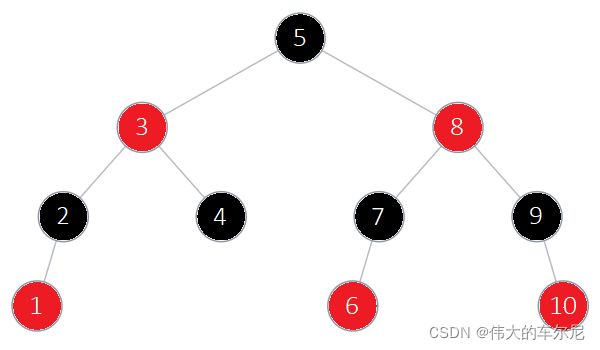
下图为一个红黑树。
在插入和删除操作时,需要通过旋转和着色操作维护红黑树的性质。
由于红黑树中没有平衡因子,因此红黑树不像 AVL 树严格平衡,但是和 AVL 树相比,维护红黑树性质的代价较低,因此在各项操作的平均性能方面,红黑树优于 AVL 树。
完全二叉树和满二叉树
完全二叉树的定义是:如果二叉树除了最深一层以外,其余每一层的结点个数都达到最大值,且最深一层的结点在最左边的连续位置,则这样的二叉树是完全二叉树。假设完全二叉树有 l l l 层和 n n n 个结点,且根结点位于第 0 0 0 层,则完全二叉树具有以下性质。
- 对于 0 ≤ i < n − 1 0 \le i < n - 1 0≤i<n−1,第 i i i 层有 2 i 2^i 2i 个结点。
- 最深一层为第 n − 1 n - 1 n−1 层,最深一层的结点数范围是 [ 1 , 2 n − 1 ] [1, 2^{n - 1}] [1,2n−1]。
- 层数 l l l 和结点数 n n n 之间的关系为: l = ⌊ log 2 n ⌋ + 1 l = \lfloor \log_2 n \rfloor + 1 l=⌊log2n⌋+1。
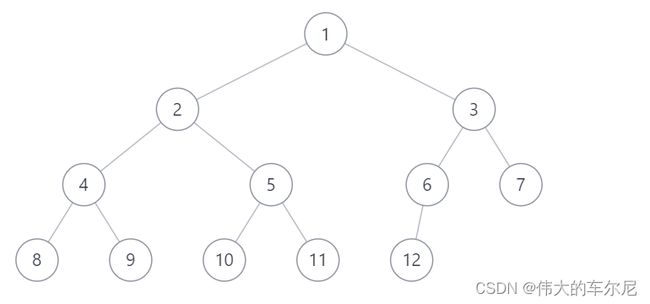
下图为一个完全二叉树。
满二叉树的定义是:如果二叉树的每一层的结点个数都达到最大值,则这样的二叉树是满二叉树。根据定义可知,满二叉树是特殊的完全二叉树。假设满二叉树有 l l l 层和 n n n 个结点,且根结点位于第 0 0 0 层,则满二叉树具有以下性质。
- 对于 0 ≤ i < n 0 \le i < n 0≤i<n,第 i i i 层有 2 i 2^i 2i 个结点。
- 层数 l l l 和结点数 n n n 之间的关系为: l = log 2 ( n + 1 ) l = \log_2 (n + 1) l=log2(n+1), n = 2 l − 1 n = 2^l - 1 n=2l−1。
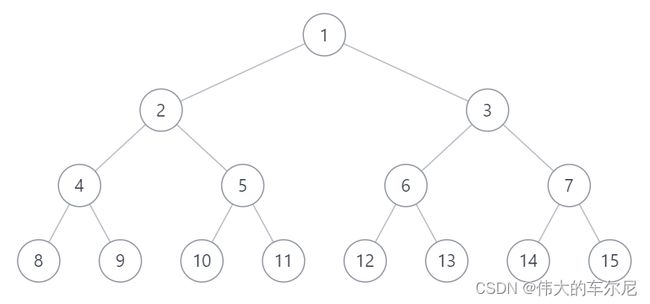
下图为一个满二叉树。
哈夫曼树
在介绍哈夫曼树之前,首先需要介绍带权值二叉树。带权值的二叉树中,每个结点都有一个权值,一个结点的带权路径长度为从根结点到该结点的路径长度(路径包含的边数,或者路径上的结点数减 1 1 1)与该结点的权值的乘积。
如果一个带权值二叉树满足所有叶结点的带权路径长度之和最小,则称为哈夫曼树或最优二叉树。哈夫曼树的特点是权值大的结点离根结点近,权值小的结点离根结点远。
哈夫曼树的常见应用是文件压缩,将每个字符转成二进制表示,从而达到减少压缩文件空间的目的。为了能在压缩文件之后解压缩得到原始文件,必须使用无损压缩,因此必须满足以下两点要求。
- 压缩文件中必须存储哈夫曼树,哈夫曼树是解压缩文件恢复原始字符的依据。
- 根据二进制表示解压缩得到的结果必须是唯一的,不能存在歧义,因此任何一个字符的二进制表示都不能是另一个字符的二进制表示的前缀。
使用哈夫曼树实现文件的压缩和解压缩的做法如下。
- 统计文件中每个字符的出现频率。
- 将每个字符的出现频率作为权值,构建哈夫曼树,得到每个字符对应的二进制表示,称为哈夫曼编码。
- 在压缩文件中存储生成的哈夫曼树,然后将每个字符对应的哈夫曼编码依次写入压缩文件中。
- 解压缩文件时,首先从压缩后的文件中取出哈夫曼树,然后遍历压缩文件中的二进制表示,根据哈夫曼树恢复原文件的每个字符。
哈夫曼树的构建方法为自底向上。初始时,每个字符对应一个结点,结点的权值为字符的出现频率。每次选两个权值最低的结点,创建新结点,新结点的两个子结点为两个权值最低的结点,新结点的权值为两个权值最低的结点之和,用新结点代替两个权值最低的结点。重复该过程,直到最后剩下一个结点,该结点是哈夫曼树的根结点,此时哈夫曼树构造完成。
以下用一个例子说明哈夫曼树的构建。
假设一个文件中有 5 5 5 种不同的字符,其中字符 a \text{a} a 出现 11 11 11 次,字符 b \text{b} b 出现 13 13 13 次,字符 c \text{c} c 出现 22 22 22 次,字符 d \text{d} d 出现 23 23 23 次,字符 e \text{e} e 出现 31 31 31 次。
- 初始时有 5 5 5 个结点:结点 a \text{a} a 的权值是 11 11 11,结点 b \text{b} b 的权值是 13 13 13,结点 c \text{c} c 的权值是 22 22 22,结点 d \text{d} d 的权值是 23 23 23,结点 e \text{e} e 的权值是 31 31 31。
- 权值最低的两个结点是 a \text{a} a 和 b \text{b} b,根据这两个结点创建新结点 ab \text{ab} ab,新结点的权值是 11 + 13 = 24 11 + 13 = 24 11+13=24。此时有 4 4 4 个结点:结点 c \text{c} c 的权值是 22 22 22,结点 d \text{d} d 的权值是 23 23 23,结点 ab \text{ab} ab 的权值是 24 24 24,结点 e \text{e} e 的权值是 31 31 31。
- 权值最低的两个结点是 c \text{c} c 和 d \text{d} d,根据这两个结点创建新结点 cd \text{cd} cd,新结点的权值是 22 + 23 = 45 22 + 23 = 45 22+23=45。此时有 3 3 3 个结点:结点 ab \text{ab} ab 的权值是 24 24 24,结点 e \text{e} e 的权值是 31 31 31,结点 cd \text{cd} cd 的权值是 45 45 45。
- 权值最低的两个结点是 ab \text{ab} ab 和 e \text{e} e,根据这两个结点创建新结点 abe \text{abe} abe,新结点的权值是 24 + 31 = 55 24 + 31 = 55 24+31=55。此时有 2 2 2 个结点:结点 cd \text{cd} cd 的权值是 45 45 45,结点 abe \text{abe} abe 的权值是 55 55 55。
- 剩下两个结点 cd \text{cd} cd 和 abe \text{abe} abe,根据这两个结点创建新结点 abcde \text{abcde} abcde,新结点的权值是 45 + 55 = 100 45 + 55 = 100 45+55=100。此时有 1 1 1 个结点:结点 abcde \text{abcde} abcde 的权值是 100 100 100。由于只剩 1 1 1 个结点,该结点是哈夫曼树的根结点,此时哈夫曼树构造完成。
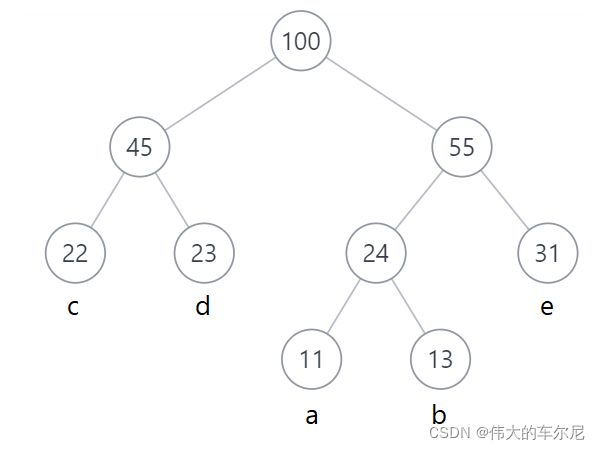
下图为根据上述例子构建的哈夫曼树。
根据构建的哈夫曼树,可以得到每个字符对应的哈夫曼编码: a = 100 \text{a} = 100 a=100, b = 101 \text{b} = 101 b=101, c = 00 \text{c} = 00 c=00, d = 01 \text{d} = 01 d=01, e = 11 \text{e} = 11 e=11。其中, a \text{a} a 和 b \text{b} b 对应的哈夫曼编码的长度是 3 3 3, c \text{c} c、 d \text{d} d 和 e \text{e} e 对应的哈夫曼编码的长度是 2 2 2,满足权值大的结点离根结点近,权值小的结点离根结点远。
多叉树
多叉树是最一般化的树结构。多叉树中的每个结点可以有任意个子结点,同一个结点的子结点之间可能有顺序关系也可能没有顺序关系,子结点之间有顺序关系的多叉树称为有序树,子结点之间没有顺序关系的多叉树称为无序树或自由树。
在 LeetCode 中定义了类 Node \texttt{Node} Node,该类定义了多叉树的一个结点。 Node \texttt{Node} Node 类的 Java 代码定义如下:
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List<Node> _children) {
val = _val;
children = _children;
}
}
多叉树的遍历有三种:前序遍历、后序遍历和层序遍历。其中,前序遍历和后序遍历基于深度优先搜索,层序遍历基于广度优先搜索。
- 前序遍历的方法为:首先遍历根结点,然后依次遍历根结点的每一个子树,对于每一个子树使用同样的方法遍历。
- 后序遍历的方法为:依次遍历根结点的每一个子树,最后遍历根结点,对于每一个子树使用同样的方法遍历。
- 层序遍历的方法为:从根结点开始,依次遍历每一层的结点。
前序遍历和后序遍历可以使用递归和迭代的方式实现。
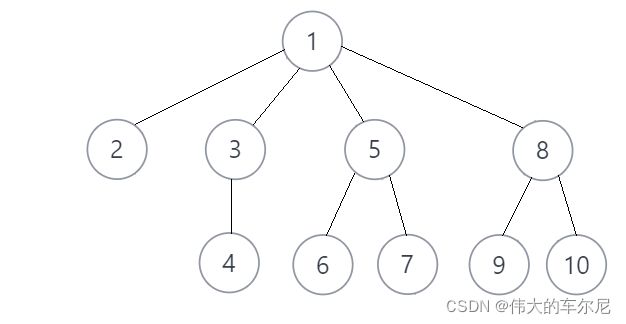
下图为一个多叉树,共有 10 10 10 个结点。
图中的多叉树的三种遍历的结果如下。
- 前序遍历: [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 ] [1,2,3,4,5,6,7,8,9,10] [1,2,3,4,5,6,7,8,9,10]。
- 后序遍历: [ 2 , 4 , 3 , 6 , 7 , 5 , 9 , 10 , 8 , 1 ] [2,4,3,6,7,5,9,10,8,1] [2,4,3,6,7,5,9,10,8,1]。
- 层序遍历: [ 1 , 2 , 3 , 5 , 8 , 4 , 6 , 7 , 9 , 10 ] [1,2,3,5,8,4,6,7,9,10] [1,2,3,5,8,4,6,7,9,10]。
B 树及其变种
B 树
B 树也称平衡多路搜索树。B 树和二叉搜索树的不同之处在于,B 树的每个结点可以有多个关键字和多个子结点。
B 树需要定义阶数,阶数至少为 2 2 2,一个 m m m 阶的 B 树具有以下性质。
- 同一个结点中的关键字按照递增顺序排列。
- 每个结点至多有 m − 1 m - 1 m−1 个关键字,每个非根结点至少有 ⌈ m 2 ⌉ − 1 \Big\lceil \dfrac{m}{2} \Big\rceil - 1 ⌈2m⌉−1 个关键字,根结点至少有 1 1 1 个关键字。
- 每个结点至多有 m m m 个子结点,每个非根且非叶结点至少有 ⌈ m 2 ⌉ \Big\lceil \dfrac{m}{2} \Big\rceil ⌈2m⌉ 个子结点,根结点如果不是叶结点则至少有 2 2 2 个子结点。
- 所有叶结点位于同一层。
- 每个关键字的两侧各有一条边指向子结点,左侧的边指向的子结点中的关键字都小于当前关键字,右侧的边指向的子结点中的关键字都大于当前关键字。
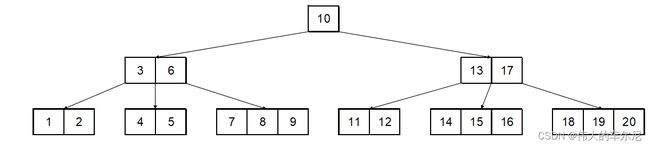
下图为一个 B 树,阶数为 4 4 4,共有 9 9 9 个结点, 20 20 20 个关键字。
在插入和删除操作时,需要通过拆分结点与合并结点操作维护 B 树的阶数性质。
B+ 树和 B* 树
B+ 树是 B 树的变种。B 树和 B+ 树有以下区别。
- B+ 树中每个结点的关键字个数和该结点的子结点个数相同。
- 所有的非叶结点存放索引信息。
- 所有的叶结点存放全部关键字。
- 所有的叶结点之间形成单向链表。
B* 树是 B+ 树的变种。B+ 树和 B* 树有以下区别。
- 不同于 B+ 树只有叶结点之间形成单向链表,B* 树的每一层结点分别形成单向链表。
- B+ 树的最低利用率是 1 2 \dfrac{1}{2} 21,B* 树的最低利用率是 2 3 \dfrac{2}{3} 32。
目录
- 二叉树题目:二叉树的前序遍历
- 二叉树题目:二叉树的中序遍历
- 二叉树题目:二叉树的后序遍历
- 二叉树题目:二叉树展开为链表
- 二叉树题目:单值二叉树
- 二叉树题目:相同的树
- 二叉树题目:对称二叉树
- 二叉树题目:翻转二叉树
- 二叉树题目:合并二叉树
- 二叉树题目:二叉树的最大深度
- 二叉树题目:二叉树的最小深度
- 二叉树题目:路径总和
- 二叉树题目:从根到叶的二进制数之和
- 二叉树题目:左叶子之和
- 二叉树题目:叶子相似的树
- 二叉树题目:二叉树的堂兄弟结点
- 二叉树题目:根据二叉树创建字符串
- 二叉树题目:二叉树的直径
- 二叉树题目:二叉树的坡度
- 二叉树题目:二叉树的层序遍历
- 二叉树题目:二叉树的层序遍历 II
- 二叉树题目:二叉树的锯齿形层序遍历
- 二叉树题目:二叉树的右视图
- 二叉树题目:填充每个结点的下一个右侧结点指针
- 二叉树题目:填充每个结点的下一个右侧结点指针 II
- 二叉树题目:二叉树的层平均值
- 二叉树题目:最大层内元素和
- 二叉树题目:层数最深叶子结点的和
- 二叉树题目:奇偶树
- 二叉树题目:翻转等价二叉树
- 二叉树题目:二叉树剪枝
- 二叉树题目:平衡二叉树
- 二叉树题目:路径总和 II
- 二叉树题目:二叉树的所有路径
- 二叉树题目:二叉树寻路
- 二叉树题目:从前序与中序遍历序列构造二叉树
- 二叉树题目:从中序与后序遍历序列构造二叉树
- 二叉树题目:最大二叉树
- 二叉树题目:最大二叉树 II
- 二叉树题目:路径总和 III
- 二叉树题目:在二叉树中增加一行
- 二叉树题目:二叉树最大宽度
- 二叉树题目:统计二叉树中好结点的数目
- 二叉树题目:二叉树的最近公共祖先
- 二叉树题目:具有所有最深结点的最小子树
- 二叉树题目:结点与其祖先之间的最大差值
- 二叉树题目:祖父结点值为偶数的结点和
- 二叉树题目:二叉树的完全性检验
- 二叉树题目:翻转二叉树以匹配前序遍历
- 二叉树题目:在受污染的二叉树中查找元素
- 二叉树题目:从前序遍历还原二叉树
- 二叉树题目:二叉树着色游戏
- 二叉树题目:输出二叉树
- 二叉树题目:分裂二叉树的最大乘积
- 二叉树题目:在二叉树中分配硬币
- 二叉树题目:根到叶路径上的不足结点
- 二叉树题目:删点成林
- 二叉树题目:好叶子结点对的数量
- 二叉树题目:完全二叉树插入器
- 二叉树题目:从前序与后序遍历序列构造二叉树
- 二叉树题目:寻找重复的子树
- 二叉树题目:二叉树的序列化与反序列化
- 二叉搜索树操作题目:二叉搜索树中的搜索操作
- 二叉搜索树操作题目:二叉搜索树中的插入操作
- 二叉搜索树操作题目:删除二叉搜索树中的结点
- 二叉搜索树题目:二叉搜索树的最近公共祖先
- 二叉搜索树题目:验证二叉搜索树
- 二叉搜索树题目:二叉搜索树的最小绝对差
- 二叉搜索树题目:递增顺序搜索树
- 二叉搜索树题目:修剪二叉搜索树
- 二叉搜索树题目:二叉搜索树的范围和
- 二叉搜索树题目:二叉搜索树中的众数
- 二叉搜索树题目:把二叉搜索树转换为累加树
- 二叉搜索树题目:将有序数组转换为二叉搜索树
- 二叉搜索树题目:二叉搜索树迭代器
- 二叉搜索树题目:前序遍历构造二叉搜索树
- 二叉搜索树题目:恢复二叉搜索树
- 二叉搜索树题目:将有序链表转换为二叉搜索树
- 二叉搜索树题目:序列化和反序列化二叉搜索树
- 多叉树题目:N 叉树的前序遍历
- 多叉树题目:N 叉树的后序遍历
- 多叉树题目:N 叉树的最大深度
- 多叉树题目:N 叉树的层序遍历
- 多叉树题目:子树中标签相同的结点数
- 多叉树题目:王位继承顺序
- 多叉树题目:收集树上所有苹果的最少时间