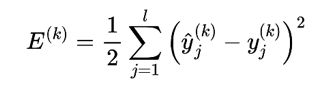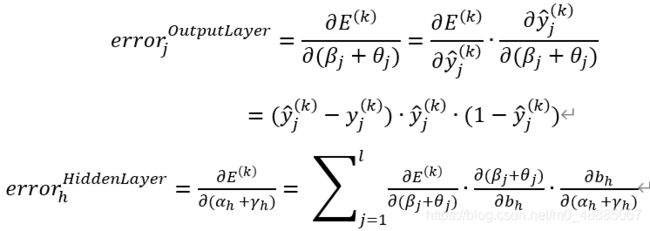“系统建模与辨识数据库”系统辨识－伊利湖问题建模
“系统建模与辨识数据库”系统辨识－伊利湖问题建模
- 一、 辨识问题的理解
-
- 1、辨识的验前知识
- 2、个人的理解与方法思考
- 二、 基于反向传播（BP）的神经网络建模方法
-
- 1、基于反向传播（BP）的神经网络建模的理论知识：
- 2、基于反向传播（BP）的神经网络算法
- 三、 辨识算法的实现（Matlab2018a）
- 四、 模型验证
-
- 法一：设置模型训练次数-100
- 法二：设置损失函数阈值(End_condition)
- 五、 结论
- 参考文献
一、 辨识问题的理解
1、辨识的验前知识
辨识问题为伊利湖西部盆地的识别，数据采样时间：1个月，样品数量：57个样品。五个输入，两个输出，输入为：水温、水传导性、水碱度、三氧化氮、总硬度。输出为：溶解氧、藻类。
2、个人的理解与方法思考
伊利湖西部盆地的辨识问题为多输入多输出问题，其模型未知，模型结构未知，模型参数也未知。我首先考虑到了运用神经网络对伊利湖西部盆地进行数学模型建模，利用已知的57组数据进行反复训练，直到损失函数满足要求，这是神经网络模型的参数变为辨识得到的结果。针对多输入多输出选用基于反向传播神经网络建模方法，激励函数为sigmoid函数。其次针对多输入多输出问题，我还想到了使用多输入多输出差分方程建模的方法，但是本人对于其理解还不够深入，特别的针对多输出多输出差分方程的阶次辨识，时滞辨识的数学推到存在较大疑问，因此假设了模型阶次与时滞进行改系统辨识。
二、 基于反向传播（BP）的神经网络建模方法
1、基于反向传播（BP）的神经网络建模的理论知识：
针对多输入多输出问题，采用了基于反向传播（BP）的神经网络建模方法。设计的神经网络模型为典型的三层神经网络，包含输入层，隐层，输出层，其模型结构如下图１。
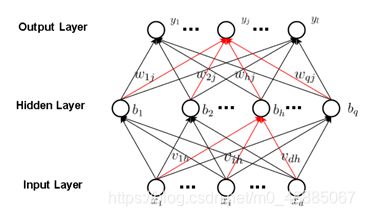
图中 x i x_i xi 为表示为第i个输入节点，数量为d个。同理， b h b_h bh 与 y j y_j yj 分别代表了隐层与输出层第h个与第j个节点，数量分别为q个与L个。
v i h v_ih vih 为输入层第i个节点与隐层第h个节点的权值， w h j w_hj whj 为隐层第h个节点与隐层第j个节点的权值。
假设系统神经模型为：
代价函数定义：
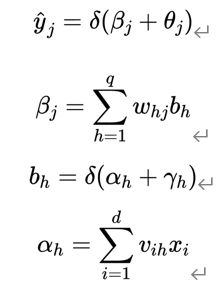
记下来只要根据代价函数不断去修正权值与参数即可，BP算法基于梯度下降策略，以目标的负梯度方向对参数进行调整，本模型有4个参数：ν_ih、 γ_h、 ω_hj 、 θ_j，因此我们需要计算如下的梯度参数：
为方便计算，引入两个过程变量：
具体的计算过程详见附件，这里只给出最终简化的结果：
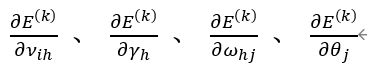
于是就可以得到如下的权值与连接权更新规则：其中η为给定学习率，也称为学习步长。
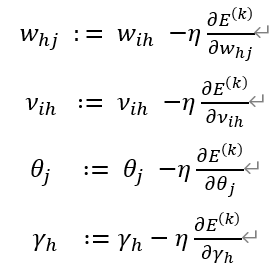
通过以上权值与连接权更新规则，对每一组输入输出数据进行训练，最终得到神经网络模型。
2、基于反向传播（BP）的神经网络算法
在上述理论基础上，总结神经网络建模的算法：
输入: 训练集
设置学习速率
步骤：
三、 辨识算法的实现（Matlab2018a）
详见链接
四、 模型验证
模型验证采用比较实际系统输出与模型输出之前的残差，通过增加训练次数，使训练得到的神经网络模型损失函数满足要求，即可得到辨识的模型。思路有两种：一种使设置神经网络模型参数辨识的损失函数阈值，一旦损失函数小于此阈值则表明神经网络网络模型达到要求，停止训练；另一种方法是设置训练次数，一旦训练次数达到要求，认定模型达到要求。
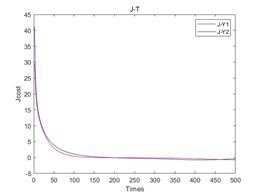
法一：设置模型训练次数-100
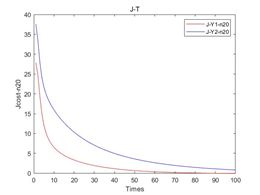
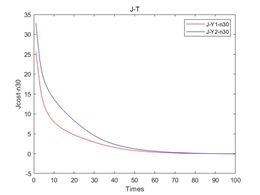
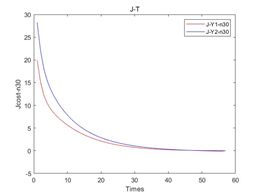
上图２中a、b、c、d分别代表了在噪声强度为0，10%、20%、30%下的损失函数。通过对所有模型进行100次训练，发现模型损失函数随着训练次数增加不断减小，最终是可以达到模型精度要求的。
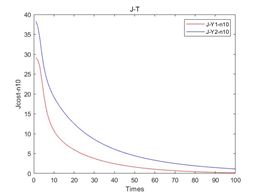
法二：设置损失函数阈值(End_condition)
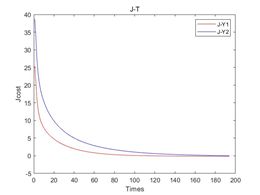
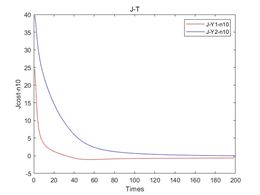
设置损失函数阈值为0.01，通过神经网络进行数据训练，最终训练次数如表所示，其损失函数如图３所示，其中图11中a、b、c、d分别代表了在噪声强度为0，10%、20%、30%下的损失函数。
| 噪声强度 | 训练次数 |
|---|---|
| 0 | 194 |
| 10% | 199 |
| 20% | 205 |
| 30% | 57 |
五、 结论
通过神经网络对伊利湖西部盆地数据进行建模，其有别于前面作业与实验的辨识方法，利用神经网络的线性、非线性特性，可建立线性、非线性系统的静态、动态、逆动态及预测模型，从而实现伊利湖西部盆地数据的建模。
本文采用的BP神经网络，其基本思想是最小二乘法，它采用梯度下降搜索方法，使网络的实际输出值与期望输出值的误差均方值为最小。通过本次建模发现BP神经网络具有以下优点：
１．不要求建立实际系统的辨识模型，即可省去系统结构建模这一步骤；
２．辨识的收敛速度不依赖于待辨识系统的维数，只与神经网络本身及其所采用的学习算法有关；
３．神经网络的连接权值在辨识中对应于模型参数，通过连接权值的调节可使网络输出逼近于系统输出；
但通过实验程序仿真也发现利用BP神经网络对伊利湖西部盆地数据进行建模的不足：
１.其辨识算法速度较慢，针对本文的５输入２输出。
２.如果目标函数存在多个极值点，容易陷入局部极小值点，这与学习速率的设置有关。
３.本次BP神经网络建模是在给定隐层数目与隐层节点数目下进行的，因此对于一般建模很难去确定神经网络层的结构，只能通过横向对比去选择最优神经网络结构。
参考文献
[1] 李玉峰,王栋栋,王博.基于BP神经网络的开关磁阻电机直接转矩控制建模与仿真[J].电子器件,2020,43(04):825-830.
[2] 刘金琨,沈晓蓉,赵龙.系统辨识理论及Matlab仿真[Ｍ].电子工业出版社,2020.9.
[3] 李言俊,张科.系统辨识理论及应用[M].国防工业出版社,2016.2.
[4] 相明辉,梁占伟,孙贻超,王新钢.基于BP神经网络的燃煤锅炉内H_2S质量浓度建模预测[J].动力工程学报,2020,40(06):433-439.
[5] 周志华.机器学习[M].清华大学出版社,2016.
[6] 李洪涛,许家俊,张明柱,王建华.基于BP神经网络的柴油发动机特性建模[J].农机化研究,2021,43(01):220-226.
“系统建模与辨识数据库”系统辨识－伊利湖问题建模-原始数据+程序+仿真截图：link.