MATLAB建模与仿真(第一章基础--第四章画图)
第一章 MATLAB建模基础
1.1 简介
通用命令
| 命令 | 说明 | 命令 | 说明 |
|---|---|---|---|
| cd | 改变当前目录 | clc | 清除命令行窗口的内容 |
| clear | 清除变量 | type | 显示文件内容 |
| edit | 打开M文件编辑器 | mkdir | 创建目录 |
| what | 显示当前目录下的M文件、MAT和MEX文件 | exit、quit | 关闭MATLAB |
| save | 保存变量到磁盘 | load | 从磁盘调入数据变量 |
| who | 列出工作空间中的变量名 | whos | 显示变量的详细信息 |
| which | 函数或文件的位置 | help | 获取函数的帮助信息 |
| pack | 收集内存碎片 | path或genpath | 显示搜索路径 |
| clf | 清除图形窗口的内容 | delete | 删除文件 |
| 标点符号 | 说明 | 标点符号 | 说明 |
|---|---|---|---|
| : | 多种应用 | ; | 区分矩阵的行或取消运行结果的显示 |
| , | 区分矩阵的列 | () | 指定运算的顺序 |
| [] | 定义矩阵 | {} | 构造单元数组 |
| @ | 构建函数句柄 | . | 小数点或对象的域访问 |
| … | 父目录 | … | 续行符号 |
| ! | 执行DOS命令 | ‘’ | 定义字符串 |
| % | 注释 |
| 键盘按键 | 说明 | 键盘按键 | 说明 |
|---|---|---|---|
| ↑ | 调出前一个命令 | ↓ | 调出后一个命令 |
| ← | 光标向右移动一个字符 | → | 光标向左移动一个字符 |
| ctrl+← | 光标向左一个单词 | ctrl+→ | 光标向右一个单词 |
| Home | 光标移动到行首 | End | 光标移动到行尾 |
| Del | 清除光标后的字符 | Backspace | 清除光标前的字符 |
| Esc | 清除当前行 | Ctrl+C | 中断正在执行的程序 |
1.2 数学建模概述
建模一般步骤
- 模型准备:
了解建模对象的实际背景,明确建模目的,搜集相关信息,掌握对象特征,形成比较清晰的问题,分析实际问题中的各种因素,并用变量表示。
- 模型假设
针对问题的特点和建模目的,做出合理的、简化的假设。对数据资料进行分析计算,找出起主要作用的因素,经过必要的精炼、简化,提出若干符合客观实际的假设。分析上述变量的关系,哪些相互依存,哪些独立,之间的关系。
- 建立模型
用数学的语言、符号描述问题。根据实际问题选用合适的数学框架,并将具体的问题在所选的数学框架中表示出来,然后发挥想象力,使用类比法,尽量采用简单的、适当的数学工具表达各变量之间的关系,建立相应的数学结构。
- 模型求解
利用各种数学方法、数学软件和计算机技术难以得出解析时借助计算机求出数值解。
- 模型分析
选取合适的算法求解所建立的数学模型表述的问题,对模型的结果进行误差分析和模型的稳定性分析。
- 模型检验
使用计算结果解决实际问题,将模型计算结果与实际现象、数据进行比较,检验模型的合理性、适用性和可靠性。
- 模型应用
通过检验,证明所建立的模型与实际应用问题相符后,则可以投入到实际应用当中,解决实际应用问题。
基本原则
- 简化原则
- 可推导原则
- 反映性远则
1.3 数学建模函数及应用
内部常见函数
| 常数名称 | 含义 | 常数名称 | 含义 |
|---|---|---|---|
| pi | 圆周率 | I或j | 虚数单位 |
| eps | 计算机中的最小数2^(-52) | inf | 无穷大 |
数学运算符
| 运算符 | 含义 | 运算符 | 含义 |
|---|---|---|---|
| .* | 数组乘法 | ./ | 数组左除 |
内部数学函数
| 函数 | 含义 | 函数 | 含义 |
|---|---|---|---|
| sqrt | 算数平方根 | abs | 绝对值函数、复数模 |
| 对数函数 | 实部函数 | real | |
| 虚部函数 | imag | ||
| 求复数辐角 | angle | ||
| 求复数的共轭复数 | conj |
数学建模应用
| 方法名称 | 具体应用场景 |
|---|---|
| 常规方法 | 数据处理(数据预处理,数值计算,数据拟合)、图形图像绘制、建议预测 |
| 规划问题解法 | 多约束线性规划、整体规划、整数规划和不太复杂的多约束非线性规划 |
| 灰色预测 | 数据量较少的情况下预测 |
| 遗传算法 | 求解多约束规划模型、训练人工神经网络 |
| 粒子群算法 | 求解无约束多元线性规划模型、训练人工神经网络 |
| 人工神经网络 | 数学建模中的一切聚类、评价及模式预测的问题 |
| 蚁群算法 | NP问题、旅行商问题、智能组卷系统 |
| 小波分析 | 海量数据趋势挖掘、组建小波神经网络 |
| 模拟退火算法 | 经典TSP问题、背包问题,求解复杂多约束非线性规划模型 |
| 计算机虚拟 | 动态(动画)展现的数学模型、动态系统仿真、复杂飞翔行规划问题粗略求解 |
1.4 MATLAB外部接口
- 在MATLAB中调用其他的语言编写的代码
- 在其他语言程序中调用MATLAB
数据文件I/O操作函数
| 函数名 | 含义 |
|---|---|
| fopen | 打开文件 |
| fclose | 关闭文件 |
| fgetl | 读文件的行,忽略回行符 |
| fgets | 读文件的行,包括回行符 |
| fread | 读取二进制文件的数据 |
| fscanf | 从文件中读取格式化数据 |
| fprintf | 将数据按照指定格式写入文本文件中 |
| fwhite | 把二进制数据写到文件中 |
| ferror | 查询文件I/O错误状态 |
打开文件
- 使用
fopen函数打开二进制形式的文件
fid = fopen(filename , permission)
[fid , message] = fopen(filename , permission)
%fid参数表示文件操作的状态及标识已打开的文件,返回值大于0,则说明文件打开成功
%filename表示待打开的数据文件,注意文件名要有扩展名
%message参数用来表示文件操作的相关信息
%permission参数用来表示文件处理方式

当文件以文本形式打开时,需要在上述指定的permission字符(串)后加字符t,如rt、wt等
%打开sin函数、cos函数以及不存在的sincos函数对应文件
[fid1,message1] = fopen('sin.m','r')
[fid2,message2] = fopen('cos.m','r')
[fid3,message3] = fopen('sincos.m','r')
为了后续操作的顺利进行,程序设计中每次打开文件,都要进行该操作是否正确的判断
[fid,message] = fopen(filename,'r');
if fid == -1
disp(message);
end
关闭文件
status=fclose(fid)
fid参数即为要关闭文件的文件标识,也是打开该文件时的返回值。成功则返回值为0,否则为-1.
fid = fopen('sin.m','r')
status = fclose(fid)
读取文件
使用fread函数读取二进制文件的数据,并将文本内容看成一个整数序列,存入矩阵
a = fread(fid)
a = fread(fid,size)
a = fread(fid,size,precision)
%fid参数是打开文件时得到的文件标识
%size参数表示读取整数的个数
%precision参数表示读取的数据类型,默认情况是uchar(即8位字符型)
写入文件
使用fwhite函数实现将二进制数据写入已打开的文件
count = fwhite(fid,a,precision)
%例
A=[1 2 3;7 8 9;4 5 6];
fid=fopen('example1_4.txt','w');
count=fwrite(fid,A,'int32')
count =
9
>> closestatus=fclose(fid)
closestatus =
0
>> fid=fopen('example1_4.txt','r');
>> A=fread(fid,[3 4],'int32');
>> closestatus=fclose(fid);
>> B=magic(3);
>> C=A*B
C =
26 38 26
116 128 116
71 83 71
普通形式读取文件
使用fgetl函数和fgets函数实现将文本的某一行读出,并将该行的内容以字符串的形式返回。fgetl忽略回行符,fgets保留回行符。
tline=fgetl(fid)
tline=fgets(fid)
>> fid=fopen('sinc.m')
fid =
5
>> while 1
tline=fgetl(fid);
if~ischar(tline)
break;
else
disp(tline)
end
end
function y=sinc(x)
i=find(x==0);
x(i)=1;
y=sin(pi*x)./(pi*x);
y(i)=1;
>> fclose(fid);
>>
假如已知写入时的格式,想要按照写入时的格式将文件内容完整读出,则可以使用fsancf函数实现已知格式文件的读取,当确定文件的ASCII码格式时,用fsanf进行精确读取
a=fscanf(fid,format)
a=fscanf(fid,format,size)
[a,count]=fscanf(fid,format,size)
format用于指定读取数据的格式
| 选项 | 读取数据的格式 |
|---|---|
| %s | 按字符串进行输入转换 |
| %d | 按十进制数据进行转换 |
| %f | 按浮点数进行转换 |
fid=fopen('example1_6.m','r');
>> d1=fscanf(fid,'%s',[5 6])
fclose(fid);
fid=fopen('example1_6.m','r');
>> d2=fscanf(fid,'%f',[5 6])
fclose(fid);
fid=fopen('example1_6.m','r');
>> d=fscanf(fid,'%f');
>d3=d'
fclose(fid);
fprintf函数写入文件
将数据按给定格式写入文件
count=fprintf(fid,format,y)
| format格式 | 数据格式 |
|---|---|
| %e | 科学计数格式 |
| %f | 固定小数点位置的数据形式 |
| %g | 在上述两个中自动选择较短的格式 |
第二章 MATLAB数值与符号计算
基本数据类型(单精度类型、双精度类型、整数类型),字符串,函数句柄,逻辑类型
2.1 数据类型
字符串类型
1.字符串的创建
>> a=135
a =
135
>> class(a)
ans =
'double'
>> size(a)
ans =
1 1
>> b='135'
b =
'135'
>> class(b)
ans =
'char'
>> size(b)
ans =
1 3
>>
字符串的基本操作
1.字符串利用“[ ]”进行拼接
2.操作函数
| 函数名 | 说明 |
|---|---|
| char | 创建字符串,将数值转变为字符串 |
| double | 将字符串转变为Unicode数值 |
| blanks | 空白字符串的创建 |
| deblank | 删除字符串尾部空格 |
| ischar | 判断变量是否字符串 |
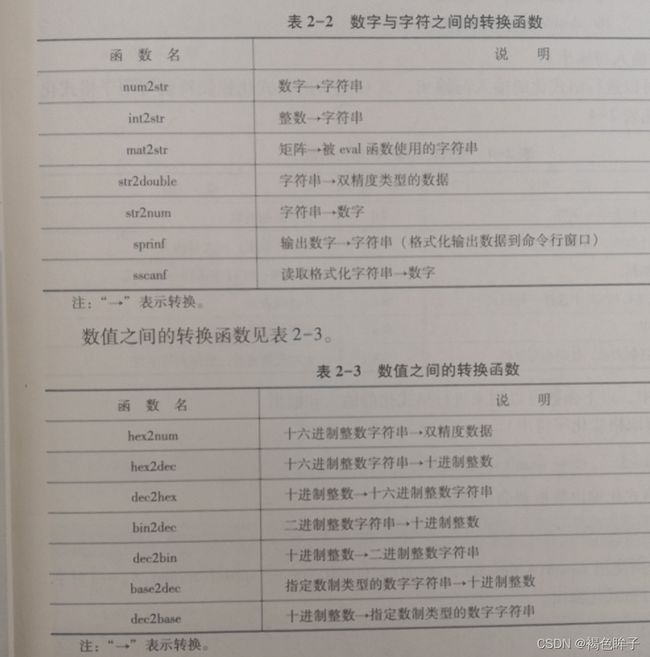
字符串转换函数
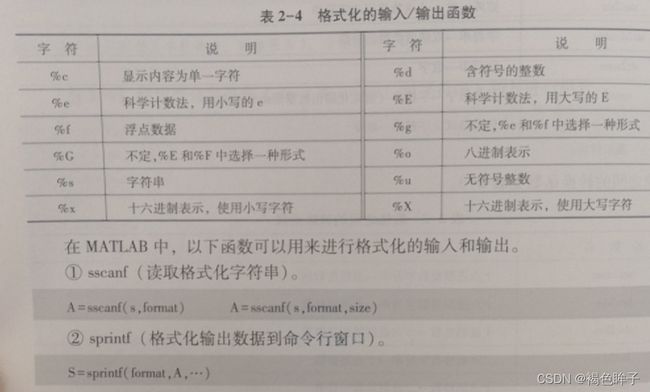
格式化的输入与输出
数值类型
1.基本数值类型

2.整数类型数据运算

3.常量

4.空数组
>> a=reshape(1:20,5,4)
a =
1 6 11 16
2 7 12 17
3 8 13 18
4 9 14 19
5 10 15 20
>> %删除第2,3行
>> a([2,3],:)=[]
a =
1 6 11 16
4 9 14 19
5 10 15 20
函数句柄
优点: 可靠性强;效率高;速度快
创建如下:
fhandle=@function_filename
逻辑类型
1.关系运算分为两类:
传统的集合运算:并集、差集和交集
专业的关系运算:选择、投影、连接和除法
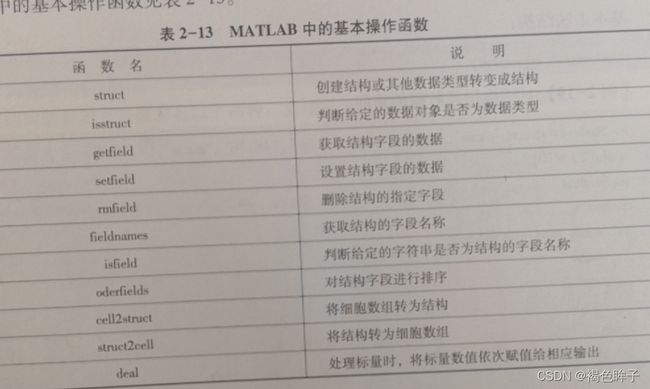
结构类型
1.创建结构
1.直接赋值法:直接使用结构的名称并配合“
.”操作符和对应的字段名称进行结构的创建。在创建时是直接给字段赋上具体的值。
>> Student.name='Jack';
>> Student.age=18;
>> Student.grade=uint16(1);
>> whos
Name Size Bytes Class Attributes
Student 1x1 546 struct
>> Student
Student =
包含以下字段的 struct:
name: 'Jack'
age: 18
grade: 1
2.使用
struct函数创建法
struct-name=struct(field1,val1,field2,val2,...)
struct-name=struct(field1,{val1},field2,{val2},...)
同时可使用repmat函数给结构制作副本
>> Student=struct('name','Jack','age',18,'grade',uint16(1))
Student =
包含以下字段的 struct:
name: 'Jack'
age: 18
grade: 1
>> Student=struct('name',{'Jack','Mike'},'age',{18,16},'grade',{4,2})
Student =
包含以下字段的 1×2 struct 数组:
name
age
grade
>> whos
Name Size Bytes Class Attributes
Student 1x2 912 struct
>> clear
>> clc
>> Student=repmat(struct('name','Jack','age',18,'grade',uint16(1)),1,2)
Student =
包含以下字段的 1×2 struct 数组:
name
age
grade
>> Student=repmat(struct('name','Jack','age',18,'grade',uint16(1)),1,3)
Student =
包含以下字段的 1×3 struct 数组:
name
age
grade
>> Student(1)
ans =
包含以下字段的 struct:
name: 'Jack'
age: 18
grade: 1
细胞数组类型
| 内容 | 细胞数组对象 | 结构数组对象 |
|---|---|---|
| 基本元素 | 细胞 | 结构 |
| 基本索引 | 全下标方式、单下标方式 | 全下标方式、单下标方式 |
| 包含的数据类型 | 任何数据类型 | 任何数据类型 |
| 数据的存储 | 细胞 | 字段 |
| 访问元素的方法 | 花括号和索引 | 圆括号、索引和字段名 |
1.创建细胞数组
1.对不同类型和尺寸的数据可以使用运算符“
{}”进行组合,以此构成细胞数组。
2.将数组中的每个元素使用“{}”括起来,接着使用数组创建符号“[]”进行组合,以此构成细胞数组。
3.使用“{}”创建一个细胞数组,MATLAB可自动扩展数组尺寸,若没有赋值,则可以作为空细胞数组存在。
4.使用cell函数创建细胞数组,该函数可以创建一维、二维或者多维细胞数组,但都为空细胞数组。
>> A={zeros(3,3,3),'A';1.23,1:10}
A =
2×2 cell 数组
{3×3×3 double} {'A' }
{[ 1.2300]} {1×10 double}
>> B=[{zeros(2,2,2)},{'B'};{1.23},{1:10}]
B =
2×2 cell 数组
{2×2×2 double} {'B' }
{[ 1.2300]} {1×10 double}
>> C={3}
C =
1×1 cell 数组
{[3]}
>> D=cell(2,3)
D =
2×3 cell 数组
{0×0 double} {0×0 double} {0×0 double}
{0×0 double} {0×0 double} {0×0 double}
2.细胞数组的基本操作
1.访问细胞数组:获得细胞数组数据,使用“
()”;获得字符串数据,使用“{}”。
a=[{zeros(3,3,3)},{'Jack'};{1.23},{1:10}]
a =
2×2 cell 数组
{3×3×3 double} {'Jack' }
{[ 1.2300]} {1×10 double}
>> d=a{1,2}(4)
d =
'k'
>> e=a{2,2}(6:end)
e =
6 7 8 9 10
>> class(e)
ans =
'double'
>> whos
Name Size Bytes Class Attributes
a 2x2 760 cell
ans 1x6 12 char
d 1x1 2 char
e 1x5 40 double
2.扩充细胞数组
>> a=[{zeros(3,3,3)},{'Jack'};{1.23},{1:10}]
a =
2×2 cell 数组
{3×3×3 double} {'Jack' }
{[ 1.2300]} {1×10 double}
>> b=cell(2)
b =
2×2 cell 数组
{0×0 double} {0×0 double}
{0×0 double} {0×0 double}
>> b(:,1)={char('Jack','Welcome');10:-1:5}
b =
2×2 cell 数组
{2×7 char } {0×0 double}
{1×6 double} {0×0 double}
>> c=[a,b]
c =
2×4 cell 数组
{3×3×3 double} {'Jack' } {2×7 char } {0×0 double}
{[ 1.2300]} {1×10 double} {1×6 double} {0×0 double}
>> d=[a,b;c]
d =
4×4 cell 数组
{3×3×3 double} {'Jack' } {2×7 char } {0×0 double}
{[ 1.2300]} {1×10 double} {1×6 double} {0×0 double}
{3×3×3 double} {'Jack' } {2×7 char } {0×0 double}
{[ 1.2300]} {1×10 double} {1×6 double} {0×0 double}
3.收缩和重组细胞数组
>> %收缩
>> d(2,:)=[]
d =
3×4 cell 数组
{3×3×3 double} {'Jack' } {2×7 char } {0×0 double}
{3×3×3 double} {'Jack' } {2×7 char } {0×0 double}
{[ 1.2300]} {1×10 double} {1×6 double} {0×0 double}
>> %重组
>> e=reshape(d,2,2,3)
2×2×3 cell 数组
e(:,:,1) =
{3×3×3 double} {[1.2300]}
{3×3×3 double} {'Jack' }
e(:,:,2) =
{'Jack' } {2×7 char}
{1×10 double} {2×7 char}
e(:,:,3) =
{1×6 double} {0×0 double}
{0×0 double} {0×0 double}
%cell2mat 函数
>> A={[1] [2 3 4];[5;6] [7 8 9;10 11 12]}
A =
2×2 cell 数组
{[ 1]} {1×3 double}
{2×1 double} {2×3 double}
>> b=cell2mat(A)
b =
1 2 3 4
5 7 8 9
6 10 11 12
>> %mat2ell 函数
>> X=[1 2 3;4 5 6;7 8 9]
X =
1 2 3
4 5 6
7 8 9
>> Y=mat2cell(X,[1 2],[1 2])
Y =
2×2 cell 数组
{[ 1]} {1×2 double}
{2×1 double} {2×2 double}
>> %num2cell 函数
>> num2cell(X)
ans =
3×3 cell 数组
{[1]} {[2]} {[3]}
{[4]} {[5]} {[6]}
{[7]} {[8]} {[9]}
>> clear
>> clc
>> A={rand(3,3,3),'Jack',pi;magic(3),1+2i,1.23}
A =
2×3 cell 数组
{3×3×3 double} {'Jack' } {[3.1416]}
{3×3 double} {[1.0000 + 2.0000i]} {[1.2300]}
>> %celldisp 函数
>> celldisp(A)
A{1,1} =
(:,:,1) =
0.8001 0.1818 0.1361
0.4314 0.2638 0.8693
0.9106 0.1455 0.5797
(:,:,2) =
0.5499 0.6221 0.4018
0.1450 0.3510 0.0760
0.8530 0.5132 0.2399
(:,:,3) =
0.1233 0.4173 0.9448
0.1839 0.0497 0.4909
0.2400 0.9027 0.4893
A{2,1} =
8 1 6
3 5 7
4 9 2
A{1,2} =
Jack
A{2,2} =
1.0000 + 2.0000i
A{1,3} =
3.1416
A{2,3} =
1.2300
>> %cellplot 函数
>> cellplot(A)
2.2 数组
相同数据类型的元素按一定的顺序排列的集合称为数组。
数组创建
数组名=起始值:增量:结束值
>> A=[1,2,3,4]
A =
1 2 3 4
>> A=1:2:8
A =
1 3 5 7
>> A=[1;2]
A =
1
2
>> A=[2 2+i 2-i];
>> B=A'
B =
2.0000 + 0.0000i
2.0000 - 1.0000i
2.0000 + 1.0000i
数组操作
1.数组寻址
对一个m行n列的数组,i表示行的索引、j表示列的索引。对二维数组的寻址可以表示为A(i,j);若采用单下标寻址,则数组中元素的下标k表示为(j-1)*m+i
>> A=randn(1,4)
A =
-0.7982 1.0187 -0.1332 -0.7145
>> A(2)
ans =
1.0187
>> A([1 2])
ans =
-0.7982 1.0187
>> A(3:end)
ans =
-0.1332 -0.7145
2.数组元素的删除
>> A=rand(3,3)
A =
0.7803 0.4039 0.9421
0.3897 0.0965 0.9561
0.2417 0.1320 0.5752
>> A([1],:)=[]
A =
0.3897 0.0965 0.9561
0.2417 0.1320 0.5752
3.数组查找和排序
查找
| 语法 | 说明 |
|---|---|
| indices=find(A) | 找出矩阵A中所有的非零元素,将这些元素的线性索引值返回到向量indices中 |
| indices=find(A,k) | 返回第一个非零元素k的索引值 |
| indices=find(A,k,‘first’) | 返回第一个非零元素k的索引值 |
| indices=find(A,k,‘last’) | 返回最后一个非零元素k的索引值 |
| [i,j]=find(…) | 返回矩阵A中非零元素的行和列的索引值 |
| [i,j,v]=find(…) | 返回矩阵A中非零元素的值v,同时返回行和列的索引值 |
注:indices表示非零元素的下标值,i,j分别表示行下列和列下列,v表示非零元素
排序
B=sort(A)
B=sort(A,dim)
B=sort(...,mode)
[B,IX]=sort(...)
A为输入等待排序的数组,B为返回的排序后的数组,当A为多维数组时,dim表示排序的维数;mode表示排序的方式,取值为升序(ascend)或降序(descend),默认排序方法为升序;IX表示存储排序后的下标数组。
>> A=[1 3 4;-3 6 4;3 5 9]
A =
1 3 4
-3 6 4
3 5 9
>> sort(A,1)
ans =
-3 3 4
1 5 4
3 6 9
>> sort(A,1,'descend')
ans =
3 6 9
1 5 4
-3 3 4
4.数组运算
>> a=magic(3);
>> a=magic(3)
a =
8 1 6
3 5 7
4 9 2
>> b=ones(3,3)
b =
1 1 1
1 1 1
1 1 1
>> c=a+b
c =
9 2 7
4 6 8
5 10 3
>> d=a.*b
d =
8 1 6
3 5 7
4 9 2
>> e=(a.^b)-c
e =
-1 -1 -1
-1 -1 -1
-1 -1 -1
2.3 矩阵
矩阵的创建
1.直接输入法[ ; ; ]
2.在M文件中建立(适合较大且复杂的矩阵)
3.从外部文件装入
已知文件所在目录为
C:\.....,在命令行窗口输入“load(C:\)”,即可创建该矩阵。
>> %生成0矩阵
>> zeros(2,3)
ans =
0 0 0
0 0 0
>> %生成[10,20]内均匀分布的3阶随机矩阵
>> a=10+(20-10)*rand(5)
a =
10.5978 10.4302 14.5092 16.8678 10.8113
12.3478 11.6899 15.4701 11.8351 19.2939
13.5316 16.4912 12.9632 13.6848 17.7571
18.2119 17.3172 17.4469 16.2562 14.8679
10.1540 16.4775 11.8896 17.8023 14.3586
>> %获取对角线元素
>> diag(a)
ans =
10.5978
11.6899
12.9632
16.2562
14.3586
>> %生成3阶帕斯卡矩阵
>> b=pascal(3)
b =
1 1 1
1 2 3
1 3 6
>> %生成3阶希尔伯特矩阵
>> format rat %以有理形式输出
>> e=hilb(3)
e =
1 1/2 1/3
1/2 1/3 1/4
1/3 1/4 1/5
矩阵运算
1.矩阵算术运算
1.加减运算:
+-
2.乘法运算:*
3.除法运算:/ \
4.乘方和开方:^ sqrtm
5.指数和对数运算:expm logm
6.转置运算
7.点运算:对应元素的运算
>> A=[1 2 3;4 5 6;7 8 9];
>> B=magic(3);
>> C=[1;2;3];
>> A+B
ans =
9 3 9
7 10 13
11 17 11
>> D=A*C
D =
14
32
50
>> E=A/B
E =
-1/30 7/15 -1/30
1/6 2/3 1/6
11/30 13/15 11/30
>> F=A^2
F =
30 36 42
66 81 96
102 126 150
>> A.^2
ans =
1 4 9
16 25 36
49 64 81
关系运算
1.当比较量为标量时,可以直接比较两数的大小。若关系成立,则关系表达式结果为1,否则为0。
2.比较量是两个维数相同的矩阵时,则是相同位置的元素按标量关系运算规则进行逐个比较。最终的关系运算的结果是一个与原矩阵维数相同的矩阵,元素由0或1组成。
3.一个标量,一个矩阵,每个元素按标量比较。
| 运算符 | 运算符 |
|---|---|
| == | ~= |
| > | < |
| >= | <= |
稀疏矩阵及其运算
2.4 多项式
多项式的创建与操作
1.直接法创建多项式
poly2sym(p)函数
>> A=[1 2 3 4 5]
A =
1 2 3 4 5
>> y=poly2sym(A)
y =
x^4 + 2*x^3 + 3*x^2 + 4*x + 5
2.poly(AR)函数创建多项式
若已知多项式的全部根,则可以用poly函数建立该多项式;也可用该函数求矩阵的特征多项式。命令格式A=poly(x)。
若x为具有N个元素的向量,则poly(x)建立以x为其根的多项式,且将该多项式的系数赋值给向量A。若x为N×N的矩阵,则poly(x)返回一个向量赋值给A,该向量的元素为矩阵x的特征多项式的系数:A(1),A(2),A(3),…,A(N),A(N+1)。
>> A=[1 2 3;2 4 6;3 5 7]
A =
1 2 3
2 4 6
3 5 7
>> p=poly(A)
p =
1.0000 -12.0000 -4.0000 -0.0000
3.其他操作
多项式运算
1.多项式的基本运算
1.多项式加减,次数不同则低位多项式的高次系数进行补0操作,然后加减。
2.多项式乘除,k=conv(p,q)函数实现多项式的乘法运算,[k,r]=deconv(p,q)函数实现多项式的除法运算。
>> %计算多项式p和q的乘、除结果。
>> p=[1 0 2 -1 4];
>> q=[1 2 5];
>> k=conv(p,q)
k =
1 2 7 3 12 3 20
>> [a,b]=deconv(p,q)
a =
1 -2 1
b =
0 0 0 7 -1
2.求导
求多项式
p的一阶导(k=polyder(p));求多项式p与q乘积的一阶导(k=polyder(p,q));求多项式p与q相除的一阶导([k,d]=polyder(p,q))。
>> %已知p、q,求p'、(p*q)'、(p/q)'。
>> p=[1 0 2 -1 4];
>> q=[1 2 5];
>> k1=polyder(p)
k1 =
4 0 4 -1
>> k2=polyder(p,q)
k2 =
6 10 28 9 24 3
>> [k3,d]=polyder(p,q)
k3 =
2 6 20 5 12 -13
d =
1 4 14 20 25
3.求值和求根
使用y=polyval(p,x)函数实现多项式在某一点的值,其中求得的x可以是复数,也可以是矩阵。
使用x=roots(p)函数实现求解多项式的根。多项式是行向量,根是列向量。
>> p=[1 0 2 -1 4];
>> x=3;
>> polyval(p,x)
ans =
100
>> x=magic(2);
>> polyval(p,x)
ans =
6 100
288 26
>> x=roots(p)
x =
-0.7177 + 1.3651i
-0.7177 - 1.3651i
0.7177 + 1.0801i
0.7177 - 1.0801i
2.5 符号运算
符号计算指运算时,无须实现对变量进行赋值,而是将所有得到的结果以标准的符号形式表示出来。符号计算是以符号对象和符号表达式作为运算对象的表达形式,最终给出的是解析解;运算过程中不会受到计算误差累计问题的影响,其计算指令较为简单,但占用的资源较多,计算的耗时长。
符号对象的创建
sym和syms函数
1.
sym函数:
格式为符号变量名+sym('符号字符串')
>> %解方程组ax-by=1,ax+by=4,其中a、x、b、y均为符号运算量
>> a=sym('a');b=sym('b');
>> x=sym('x');
>> y=sym('y');
>> [x,y]=solve(a*x-b*y-1,a*x+b*y-4,x,y)
x =
5/(2*a)
y =
3/(2*b)
2.
syms函数:
可以定义一条语句中的多个符号变量
格式为syms 符号变量名1 符号变量名2 ... 符号变量名n
符号运算中的运算符
符号运算的精度
MATLAB符号运算工具箱中提供零种不同的算术运算。
1.数值类型:浮点算术运算
2.有理数类型:Maple的精确符号计算
3.VPA类型:Maple的任意精度算术运算
>> %浮点数和有理数运算
>> format long
>> 1/2+1/3
ans =
0.833333333333333
>> sym(1/2+1/3)
ans =
5/6
其中,浮点运算的速度最快,需要的计算机内存最小,但是计算的结果不够精确;有理数运算所需要的时间和内存都最大,只要有足够大的内存和时间,就能产生精确的运算结果。
一般符号运算的结果都是字符串。如果想要从精确解中获得任意精度的解,并改变默认精度,还需要以下函数:
1.digits(d):调用该函数后的近似解的精度变成d位有效数字,d的默认值为32。
调用不加任何参数的digits命令可以得到当前运算所采用的精度。
2.vpa(A,d):求符号解A的近似解,该近似解的有效位由参数d来定义。
如果不指定参数d,则按照digits(d)指令设置的有效位来输出计算结果。vpa函数的输入既可以是符号对象,也可以是数值对象,但是其输出为符号对象。
3.double(A):把符号矩阵或者任意精度表示的矩阵转换为双精度矩阵。
>> A=[1.100 2.300 3.500;4.900 5.400 6;9.100 7.890 4.230];
>> S=sym(A)
>>%生成的符号矩阵如下
S =
[ 11/10, 23/10, 7/2]
[ 49/10, 27/5, 6]
[ 91/10, 789/100, 423/100]
>> %转换为有效数字任意精度矩阵如下
>> digits(4)
>> vpa(A)
ans =
[ 1.1, 2.3, 3.5]
[ 4.9, 5.4, 6.0]
[ 9.1, 7.89, 4.23]
>> %转换为双精度矩阵如下
>> double(S)
ans =
1.100000000000000 2.300000000000000 3.500000000000000
4.900000000000000 5.400000000000000 6.000000000000000
9.100000000000000 7.890000000000000 4.230000000000000
2.6 符号表达式运算
可以进行数值转换、变量替换、化简和格式化等等
数值转换
>>%利用转换函数转换符号常量
>> a=3.8495;
>> f=str2sym('6*a+2^(2*a)');
>> m=eval(f)
m =
2.308895327301833e+02
>> int8(m)
ans =
int8
127
>> logical(m)
ans =
logical
1
变量变换
使用subs函数可以实现变量间的替换功能,这样可以使复杂的函数方程式在计算上变得简单。
1.subs(X,old,new):变量X中使用new变量去替换old变量,old必须是S中的符号变量。
2.subs(X,new):用new变量替换S中的自变量。
>> syms x x1 x2 x3;
>> y=1+2*x+3*x;
>> subs(y,'x','x1+2*x2+3*x3')
ans=
2*x1+4*x2+6*x3+3^(x1+2*x2+3*x3)+1
化简与格式化
1.simplify(s):对s进行简化,s既可以是多项式,也可以是符号表达式矩阵。
2.simple(s):使用MATLAB的其他函数对表达式进行综合化简,并显示化简的具体过程。
>> syms x
>> y=2*sin(x)*cos(x);
>> %直接实现化简,得出最终表达式
>> simplify(y)
ans =
sin(2*x)
>> syms x y
>> y1=x^2+2*x+1;
>> y2=x^3+2*x^2+4;
>> y3=(x+2*y)^3;
>> factor(y1)
ans =
[ x + 1, x + 1]
>> horner(y2)
ans =
x^2*(x + 2) + 4
>> expand(y3)
ans =
x^3 + 6*x^2*y + 12*x*y^2 + 8*y^3
2.7 符号矩阵的计算
符号矩阵的计算在形式上同数值计算十分相似。
基本算术运算
符号矩阵必须大小相同
>> syms a b c d
>> A=str2sym('[a b;c d]');
>> B=str2sym('[2*a 3*b;c+a d+8]');
>> A+B
ans =
[ 3*a, 4*b]
[ a + 2*c, 2*d + 8]
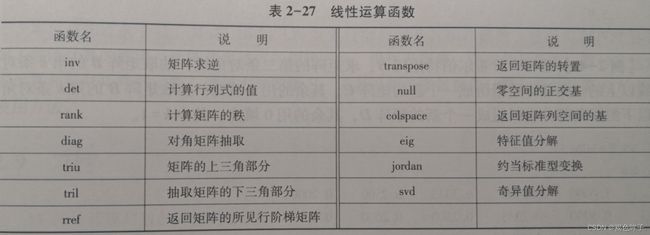
线性代数运算
>> %已知3阶魔方矩阵A,求逆、行列式、秩、列空间基和转置
>> A=magic(3)
A =
8 1 6
3 5 7
4 9 2
>> A=sym(A);
>> %求逆
>> inv(A)
ans =
[ 53/360, -13/90, 23/360]
[ -11/180, 1/45, 19/180]
[ -7/360, 17/90, -37/360]
>> %求行列式
>> det(A)
ans =
-360
>> %求秩
>> rank(A)
ans =
3
>> %求列空间基
>> colspace(A)
ans =
[ 1, 0, 0]
[ 0, 1, 0]
[ 0, 0, 1]
>> %转置
>> transpose(A)
ans =
[ 8, 3, 4]
[ 1, 5, 9]
[ 6, 7, 2]
第三章 MATLAB程序设计
3.1 M文件概述
M文件就是由一系列相关代码组成的一个扩展名为“m”的文件,其语法与其他高级程序设计语言一样。M文件具有简单、交互性好和易于调试的特点。
M文件的基本内容
定义函数名称、输入/输出变量的数量和顺序。
function[out1,out2,out3,...]=funName(in1,in2,in3,...)
%若无输出则
functionfunName(in1,in2,in3,...)
2.H1行
帮助文本的第一行称为H1行,H1行紧跟函数定义行。H1行属于帮助文本中特殊的一行。H1行的主要作用是对程序进行一行的总结。在H1行一般要包括大写的函数名和函数功能的简要介绍。
3.帮助文本
帮助文本由H1行及其后面连续的以%开头的所有注释代码行组成。该文本是对程序进行详细的说明。通常,在调用help命令查询M文件时,H1行会一起显示在窗口。使用者在编写M文件时,可建立帮助文本,将函数的功能、调用函数参数描述出来,便于使用者或别人查看函数的使用。
4.注释
5.函数体
函数体是函数和脚本中计算和处理数据的主体,是实现函数功能的主要部分,一般由具体的控制命令和MATLAB函数构成,主要是进行实际计算的代码,可以包含进行计算和赋值的语句、函数调用、循环和流控制语句,以及注释语句、空行等。
3.2 M文件的分类
M文件可以根据调用方式的不同分为以下两类:脚本文件和函数文件。脚本文件是包含多条MATLAB命令的文件;函数文件可以包含输入变量,并将结果传送给输出变量。

脚本文件
M命令文件又称M脚本文件,基本文件:
1.符号“%”起始的H1行,应包含文件名和功能简介。
2.符号“%”起始的Help文本,H1行及其之后的所有连续注释行以此构成整个在线帮助文件。
3.编写和修改目录,该区域文本内容也都有符号“%”;标志编写及修改该M文件的作者、日期和版本记录,可用于软件档案管理。
4.程序体(附带关键指令功能注释)。
函数文件
函数文件犹如一个“黑箱”,且有特定的书写规范。
M函数文件的基本结构:
1.函数声明行:位于函数文件的首行,以MATLAB关键字function开头,函数名以及函数的输入/输出量名都在这一行被定义。
2.H1行:提供lookfor关键词查询和help在线使用帮助。
3.Help文本:H1行及其之后的所有连续注释行构成整个在线帮助文本。
4.编写和修改记录:标志编写及修改该M文件的作者、日期和版本记录,可用于软件档案管理。
5.函数体:与前面的注释可以“空”行相隔。这部分内容由实现该M文件功能的MATLAB指令组成。
%编写出求取平均值与标准差的函数文件stat.m
在MATLAB命令行窗口输入“edit”,打开M文件编辑器。在M文件编辑器中输入以下代码:
>>stat.m %函数文件
function [mean1,stdev]=stat(x)
%STAT函数文件
%求阵列x的平均值和标准差
[m,n]=size(x);
if m==1
m=n;
end
s1=sum(x);
s2=sum(x.^2);
mean1=s1/m;
stdev=sqrt(s2/m-mean1^2);
在命令行窗口依次输入如下命令:
在这里插入代码片
P码文件
1.一个M文件首次被调用时,首先会进行语法分析,并把生成的相应内部伪代码(P码)文件存放在内存中。此后再调用M时,会直接调用P码。
2.P码文件的预先生成:
pcode FunName %在当前目录上生成FunName.p
pcode FunName-inplace %在FunName.m所在目录上生成FunName.p
3.内存中P码文件的列表和清除
inmem %罗列出内存中所有P码文件名
clearFunName %清除内存中的FunName.pP码文件
clear function %清除内存中的所有P码文件
在MATLAB中,查看内存中的所有P码文件,然后清除所有P码文件,再次查看内存中的P码文件信息。
>> inmem
ans =
56×1 cell 数组
{'pathdef' }
{'userpath' }
{'matlabrc' }
{'usejava' }
{'addEnabledAddonsToPath' }
{'+addons\private\addFilesFrom' }
{'settings' }
{'settings' }
{'getSettingsRoot' }
{'addInstalledSupportPackagesToPath' }
{'fullfile' }
{'getSupportPackageRootNoCreate' }
{'addFoldersToPathFrom' }
{'isdir' }
{'SupportPackageRootHandler' }
{'getSprootSettingFileLocation' }
{'filesep' }
{'ispc' }
{'SettingWriterReader' }
{'SingleRootHandler' }
{'onCleanup' }
{'opaque.char' }
{'initprefs' }
{'hgrc' }
{'ismac' }
{'ispref' }
{'uitools\private\prefutils' }
{'initdesktoputils' }
{'path' }
{'Manager' }
{'EventSource' }
{'toolboxdir' }
{'Channel' }
{'MessageHandler' }
{'InputStream' }
{'Stream' }
{'OutputStream' }
{'mdbstatus' }
{'breakpointsForAllFiles' }
{'+editor\private\createJavaBreakpointsFromDbstatus'}
{'workspacefunc' }
{'now' }
{'datenum' }
{'stringToLegacyText' }
{'FevalService' }
{'HttpService' }
{'MatlabService' }
{'callConnectorStarted' }
{'callLifecycle' }
{'Logger' }
{'LoggerLevel' }
{'exampleConnectorStarted' }
{'trackCallCount' }
{'getInstalledSupportPackagesInfo' }
{'getInstalledSpPkgProducts' }
{'repmat' }
>> clear functions
>> inmem
ans =
14×1 cell 数组
{'getSettingsRoot' }
{'onCleanup' }
{'Manager' }
{'Channel' }
{'MessageHandler' }
{'InputStream' }
{'OutputStream' }
{'workspacefunc' }
{'now' }
{'datenum' }
{'stringToLegacyText'}
{'FevalService' }
{'MatlabService' }
{'trackCallCount' }
>>
3.3 函数类型
1.命令行进行定义和保存为M文件(匿名函数)
2.使用M文件创建的函数(主函数、子函数、嵌套函数等)
主函数
主函数指在M文件中排在最前面的函数。主函数与其M文件同名,并且是唯一可以在命令行窗口或者其他函数中调用的函数。
子函数
排在主函数后面进行定义的函数,其排列没有固定的顺序。主 子 在形式上没有区别,但子函数只能在同一个文件上的主函数或者其他子函数进行调用。
子函数示例
function[avg,med]=newstats(u) %主函数
%查找内部函数的均值和中位数
n=length(u);
avg=mean(u,n);
med=median(u,n);
function a=mean(v,n) %子函数
%计算平均值
a=sum(v)/n;
function m=median(v,n) %子函数
%计算中位数
w=sort(v);
if rem(n,2)==1
m=w((n+1)/2);
else
m=(w(n/2)+w(n/2+1))/2;
end
>> newstats 5
ans =
53
调用一个子函数的查找顺序:
首先检查被调用的函数是否为M文件上的子函数,其次寻找是否有同名的私有函数,最后在搜索路径中查找其他M文件。
子函数的帮助文本
需将M文件名加在子函数名前面
helpmyfile>子函数名
私有函数
私有函数是子函数的一种,只有父M文件函数才能调用它。私有函数存放于当前目录的子目录,且名为private。
私有函数的特点:
1.私有函数只对父目录中的
M文件可见。
2.调用私有函数的M文件必须位于private子目录的直接父目录内。
设私有函数名为myprivfile,为得到私有函数的帮助信息,需输入如下命令:
help private/myprivfile
嵌套函数
某函数中定义的函数。
1.嵌套函数的创建
MATLAB允许在
M文件的函数体定义一个或多个嵌套函数,被嵌套的函数能包含进任何构成M文件的成分。
对于嵌套函数必须以end结束
1)最基本的嵌套函数结构
function x=A(p1,p2)
...
function y=B(p3)
...
end
...
end
2)平行嵌套函数结构
function x=A(p1,p2)
...
function y=B(p3)
...
end
function z=C(p4)
...
end
...
end
3)多层嵌套函数结构
function x=A(p1,p2)
...
function y=B(p3)
...
function z=C(p4)
...
end
...
end
...
end
2.嵌套函数的调用
一个嵌套函数可以被以下3种函数进行调用
1.该嵌套函数的直接上一层
2.在同一母函数下的同一级嵌套函数
3.任意低级别的函数
示例
function A(x,y)
B(x,y);
C(y);
function B(x,y)
D(x);
C(y);
function D(x)
C(x);
end
end
function C(x)
E(x);
function E(x)
...
end
end
end
函数A包含B和C,B、C嵌套D、E
1)A可调BC,不能DE
2)B可CD,不能E,C可BE,不能D
3)DE可BC,DE不能互相
3.嵌套函数中变量的使用范围
函数之间,局部变量不能共享。即子函数之间或与主函数之间是不能共享变量的,每个函数都有自己的工作空间,用于存放变量。在嵌套函数中,因为函数之间存在嵌套的关系,所以有些情况可以共享变量。
test5.m
function test5
x=5;
nestfun;
function y=nestfun
y=x+1;
end
y
end
test6.m
function test6
x=5;
z=nestfun;
function y=nestfun
y=x+1;
end
z
end
运行
>> test5
未定义函数或变量 'y'。
出错 test5 (line 7)
y
>> test6
z =
6
在test5由于在嵌套函数中尽管计算了y的值并进行了返回,但这个变量值存储在嵌套函数的工作空间无法被外层使用。在test6中将嵌套函数的赋值给了z,实现正确显示。
重载函数
它是已经存在的函数的另一个版本。在MATLAB中每一个重载函数都有一个M文件存放在MATLAB目录中。格式如下:
1)目录
\@double,输入变量数据类型为double时才可被调动
2)目录\@int32,输入变量数据类型为int32时才可被调动
3.4 程序流程控制
顺序结构
1.数据输入
A=input(提示信息,选项);
2.数据输出
disp(输出项);
3.数据的暂停
1.暂停执行,
pause
2.省略延迟时间,直接使用pause函数,暂停程序,直到用户按任意键程序继续实行
3.中止程序运行
1)创建命令文件和函数文件
%创建命令文件test3.m
f=input('Input f temperature');
c=5*(f-32)/9
%建立函数文件test4.m
function c=test4(f)
c=5*(f-32)/9
2)调用命令文件
>> test3
Input f temperature99
c =
37.2222
>> y=input('Input f temperature');
Input f temperature99
>> x=test4(y)
c =
37.2222
x =
37.2222
分支结构
- if语句(条件转换语句)
1)单分支if语句
if 条件
语句组
end
3.5 M文件调试
第四章 图形图像
二维图形
主要介绍plot、fplot、ezplot三个基本的二维图形绘制函数
基本绘图函数
1.plot函数
1)plot(y)
y为向量则以y的分量为纵坐标、元素序号为横坐标,用直线以此连接数据点,绘制曲线。
若y为实矩阵,则按列绘制每列对应的曲线。
2)plot(x,y)
1.x,y为同维向量,则x横y纵。
2.x向量,y行数或列数与x 长度相等的矩阵,则绘制多条不同色彩的连线图,x为公共横坐标。
3.x,y为同型矩阵,则以x,y对应元素分别绘制曲线,曲线条数等于矩阵列数。
3)plot(x1,y1,x2,y2,....)
每对x,y必须符合plot(x,y)的要求
>> x=linspace(-2*pi,2*pi,200);%在x轴取200个点
>> y=sin(x);
>> plot(x,sin(x),'bh',x,cos(x),'g*');

2.fplot函数
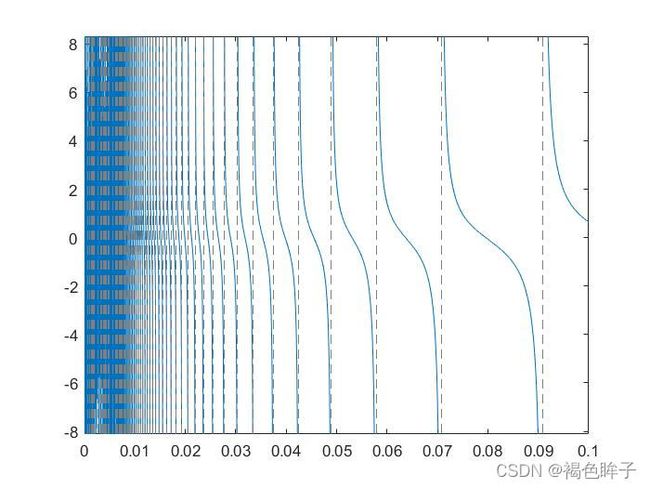
对于变化剧烈的函数,fplot函数可用来进行比较精确的绘图,对剧烈变化处进行较密集的取样。该绘图函数通过内部自适应算法来动态改变变量之间的间隔。当函数变化缓慢时,间隔相对大一点;函数变化剧烈时,间隔相对小一点。
使用格式:
fplot(function,limits)
fplot(function,limits,LineSpec)
fplot(function,limits,tol)
fplot(function,limits,tol,LineSpec)
fplot(function,limits,n)
fplot(axex_handle,...)
[X,Y]=fplot(function,limits,...)
[...]=fplot(function,limits,tol,n,LineSpec,P1,P2,...)
function为呆绘制的图形名称;limits是一个指定x轴范围的向量[xmin xmax],或者是x轴和y轴范围的向量[xmin xmax ymin ymax];LineSpec定义绘图的线条、颜色和数据点等;tol为相对误差容忍度,其默认值为2e-3;n控制图形绘制的点的数量,当n>=1时,至少绘制n+1个点,n默认值1;axex_handle为坐标轴句柄,函数图形的绘制就在这个坐标轴中显现。
例:
>> fplot('tan(1/x)',[0 0.1]); %[0 0.1]时绘图范围
3.ezplot函数
可以绘制显函数图形、隐函数图形和参数方程图形。调用格式如下:
ezplot(f)
ezplot(f,[min,max])
ezplot(f,[xmin,xmax,ymin,ymax])
ezplot(x,y)
ezplot(x,y,[tmin,tmax])
ezplot(...,figure_handle)
ezplot(axes_handle,...)
h=ezplot(...)
例:
绘制显函数 c o s x cosx cosx的二维曲线;
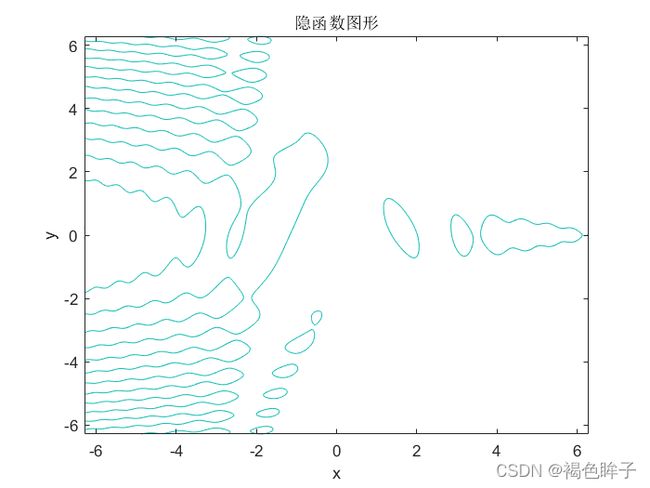
绘制隐函数 f ( x , y ) = x 2 s i n ( x + y 2 ) + y 2 e x + 6 c o s ( x 2 + y ) = 0 f(x,y)=x^2sin(x+y^2)+y^2e^x+6cos(x^2+y)=0 f(x,y)=x2sin(x+y2)+y2ex+6cos(x2+y)=0的二维曲线。
syms x;
f=cos(x);
ezplot(f);
xlabel('x');
ylabel('y');
title('cosx函数图形')
syms x;
syms y
f=x^2*sin(x+y^2)+y^2*exp(x)+6*cos(x^2+y);
ezplot(f)
xlabel('x');
ylabel('y');
title('隐函数图形')
例: 参数方程 x 2 + y 2 − 4 = 0 x^2+y^2-4=0 x2+y2−4=0在区域[-3,3,-3,3]内的图形。
ezplot('x^2+y^2-4',[-3,3,-3,3]);
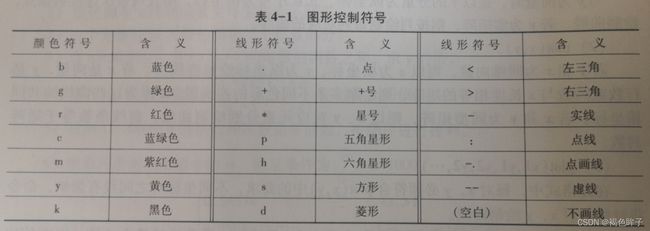
特殊函数
bar(y) %为每一个y中元素画出条形
bar(x,y) %在指定的横坐标x上画出y,其中x为严格单增的向量
bar(...,width) %设置每个条形相对距离,默认值为0.8
bar(...,'style') %定义条的形状类型,选项为'group'或者'stack'
bar(...,'bar_color') %定义条形的颜色
例:
>> y=rand(6,4); %随机生成六组数据,每组数据包含4个数据
>> bar(y); %绘制y条形图

2.饼状图:pie函数
饼状图用于表示矢量或矩阵中各元素所占有的比例。使用方法:
pie(x):使用x中的数据绘制饼图,x中的每一个元素用饼图中的一个扇区表示。
pie(x,explode):绘制向量x的饼图,如果向量x的元素和小于1,则绘制出不完全的饼图。explode为一个与x尺寸相同的矩阵,非零元素所对应的x矩阵中的元素从饼图中分离出来。
>> x=[1 3 0.5 2.5 2];
>> explode=[0 1 0 0 0];
>> pie(x,explode)
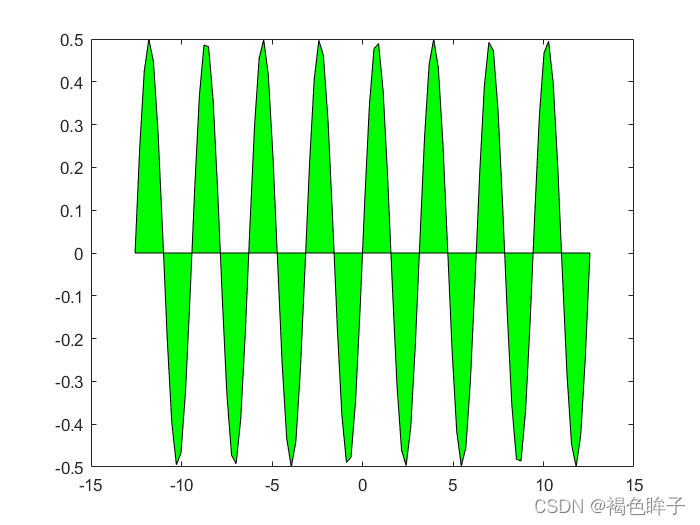
fill(X,Y,C):用X和Y中的数据生成多边形,用C指定颜色填充。C为色图向量或矩阵。若C为行向量,则要求C的维数等于X和Y的列数;若C为列向量,则要求C的维数等于X和Y的行数。
fii(X,Y,ColorSpec):用ColorSpec指定的颜色填充由X和Y定义的多边形。
fill(X1,Y1,C1,X2,Y2,C2,...):指定多个要填充的二维区域。按向量元素的下标渐增次序依次用直线段连接X,Y对应元素定义的数据点。若连线不封闭,MATLAB会自动将折线首尾连接起来,形成封闭多边形。
fill(...,'PropertyName',PropertyValue):允许用户对一个patch图形对象的某个属性设定属性值。
>> x=linespace(-4*pi,4*pi,100);%绘制区域为0~10,取100个点
未定义函数或变量 'linespace'。
是不是想输入:
>> x=linspace(-4*pi,4*pi,100);%绘制区域为0~10,取100个点
>> y=sin(x).*cos(x);
>> fill(x,y,'g');%'g'为绿色
1)
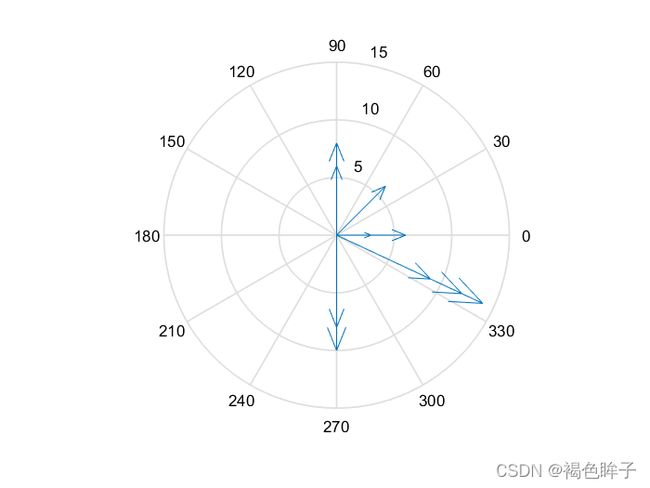
compass(x,y):函数绘制一个由原点出发、由(x,y)组成的向量箭头图形。
2)compass(z):等价于compass(real(z),imag(z))。
3)compass(...,LineSpec):用参量LineSpec指定箭头的线型、标记符号、颜色等属性。
4)h=compass(...):函数返回line对象的句柄给h。
对于表示方向的自变量,要进行角度和弧度的转换,一般格式为rad=ang*pi/180。
>> wdir=[45 90 90 45 360 335 360 270 335 270 335 335];%风向
>> knots=[6 6 8 6 3 9 6 8 9 10 14 12];%风力
>> rdir=wdir*pi/180;%将风向转换为弧度
>> [x,y]=pol2cart(rdir,knots);%极坐标和直角坐标转换
>> compass(x,y);%绘制图形
4.2 三维图形
基本绘图函数
三维曲线图(plot3/ezplot3)、三维网格图(mesh/ezmesh)、三维曲面图(surf/ezsurf)。“ez”表示函数用于绘制符号函数图形,不加表示绘制数值图形。
1.plot3/ezplot3
plot3:1.
plot3(X,Y,Z):当XYZ是长度相同的向量时,该命令将绘制以向量X、Y、Z为(x,y,z)坐标值的三维曲线;当XYZ是m×n矩阵时,将绘制m条曲线,每条曲线以X、Y、Z列向量元素(x,y,z)坐标值绘制多条曲线。
2.plot3(X,Y,Z,LineSpec):指定曲线线形颜色。
ezplot3:1.
ezplot3(x,y,z):绘制参数方程 x = x ( t ) , y = y ( t ) , z = z ( t ) x=x(t),y=y(t),z=z(t) x=x(t),y=y(t),z=z(t)的三维曲线图,t范围[0,2]。
2.ezplot3(x,y,z,[t m i n , t m a x t_{min},t_{max} tmin,tmax])
3.ezplot3(x,y,z,[t m i n , t m a x t_{min},t_{max} tmin,tmax],'animate'):空间曲线的动态轨迹。
例:
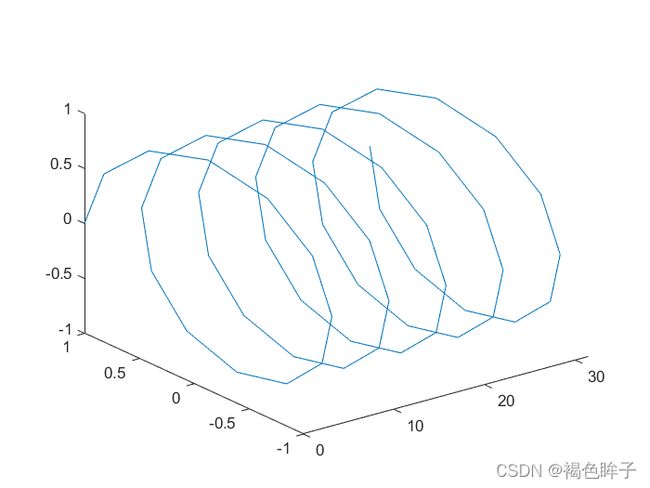
>> x=0:pi/6:10*pi;
>> y=cos(x);
>> z=sin(x);
>> plot3(x,y,z)
>> syms t;
>> x=sin(t);
>> y=cos(t);
>> z=t;
>> ezplot3(x,y,z,[0,10*pi],'animate');
mesh函数:生成由X、Y和Z指定的网线面,由C指定颜色的三维网格图。
mesh(Z):分别以矩阵Z的行、列下标作为x轴和y轴的自变量绘图。
mesh(X,Y,Z):最常用的一般调用格式。
mesh(X,Y,Z,C):C用于指定颜色,没有给定C,则默认C=Z。
ezmesh调用:
ezmesh(FUN,DOMAIN):FUN为函数表达式,DOMAIN为自变量的取值范围。
>> syms x;
>> syms t;
>> f=x*sin(t);
>> ezmesh(f,[-pi,pi]);
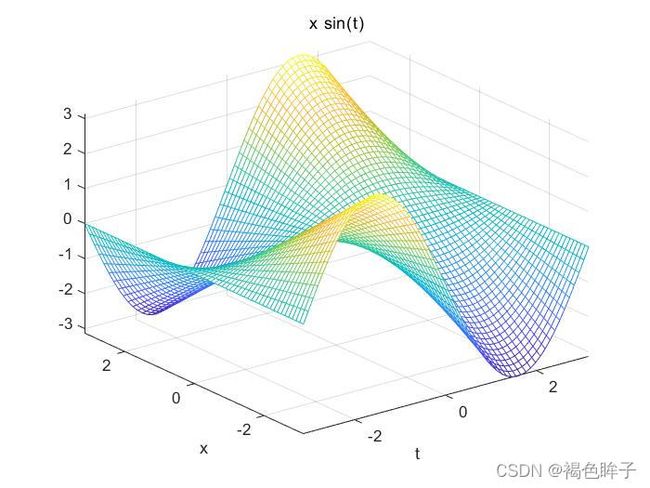
另,meshc在原图添加等高线,meshz在原图上添加绘图边界。ezmesh只有zemeshc。
3.surf/ezsurf
surf函数专门用于绘制三维着色曲线图和surfc通过矩形区域来观测数学函数的函数。
1.surf(Z):生成一个由矩阵Z确定的三维带阴影的曲面图,[m,n]=size(Z),X=n,Y=1:m。高度Z为定义在一个几何矩形区域内的单值函数,Z同时指定曲面高度数据的颜色,所以颜色相同的曲面高度是相当的。
2.surf(X,Y,Z):Z同时为曲面高度,也是颜色依据。X和Y定义X轴Y轴曲面数据。若XY为向量,length(X)=n,length(Y)=m,[m,n]=size(Z),空间曲面上的结点为(X(I),Y(j),Z(I,j))。
3.surf(X,Y,Z,C):指定颜色C。
ezsurf调用:
ezsurf(FUN,DOMAIN):FUN为函数表达式,DOMAIN为自变量取值范围。
>> x=linspace(-2,2,25);%在x轴取25个点
>> y=linspace(-2,2,25);%在y轴取25个点
>> [xx yy]=meshgrid(x,y);%xx和yy都是25×25的矩阵
>> zz=xx.*exp(-xx.^2-yy.^2);%计算函数值,zz也是25×25的矩阵
>> surf(xx,yy,zz);
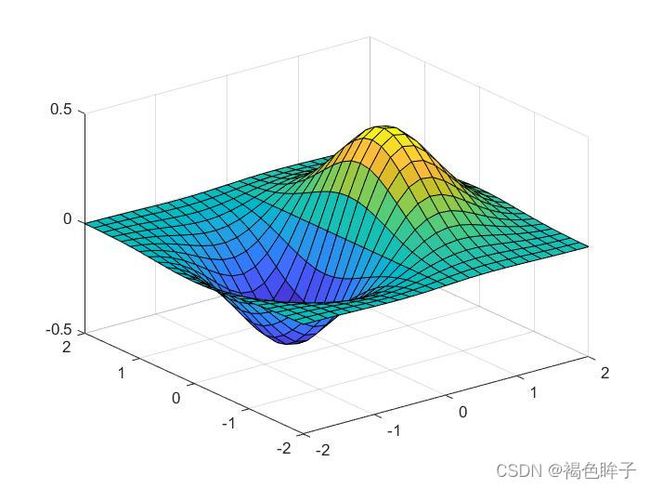
另,surf有两个扩展函数:surfc(添加等高线)和surfl(绘制带有光源的曲面图)。ezsurf只有ezsurfc函数。
特殊函数
1.pie3函数:三维饼图
pie3([2,3,4,5])%分别占比14%、21%、29%、36%
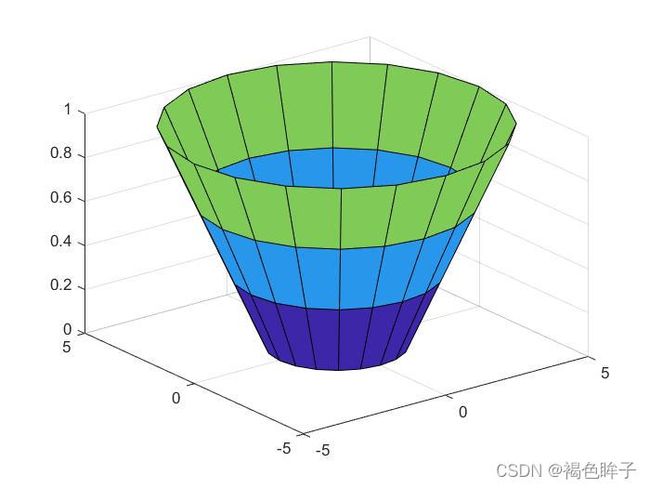
cylinder([2,3,4,5])
1)
sphere:生成三维直角坐标系中的单位球体,有20×20个面。
2)sphere(n):在当前坐标系画有n×n个面的球体。
3)[X,Y,Z]=sphere(n):返回3个阶数为(n+1)×(n+1)的直角坐标系中的坐标矩阵。可以用命令surf(X,Y,Z)或mesh(X,Y,Z)画出球体。

4.peaks函数:
可产生一个凹凸有致的曲面,包含了3个局部极大点和3个局部极小点,方程为:
y = 3 ( 1 − x ) 2 e − x 2 ( y + 1 ) 2 − 10 ( x 5 − x 3 − y 5 ) e − x 2 − y 2 − 1 3 e − ( x − 1 ) 2 − y 2 y=3(1-x)^2e^{-x^2(y+1)^2}-10(\frac{x}{5}-x^3-y^5)e^{-x^2-y^2}-\frac{1}{3}e^{-(x-1)^2-y^2} y=3(1−x)2e−x2(y+1)2−10(5x−x3−y5)e−x2−y2−31e−(x−1)2−y2
>> peaks
z = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...
- 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...
- 1/3*exp(-(x+1).^2 - y.^2)
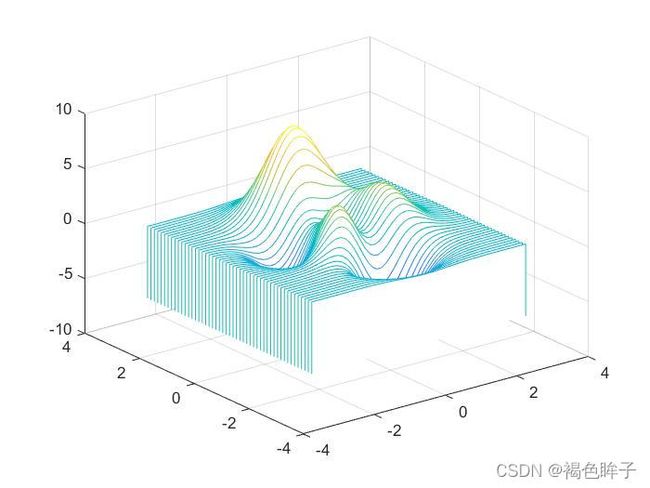
>> [x,y,z]=peaks;
>> waterfall(x,y,z);
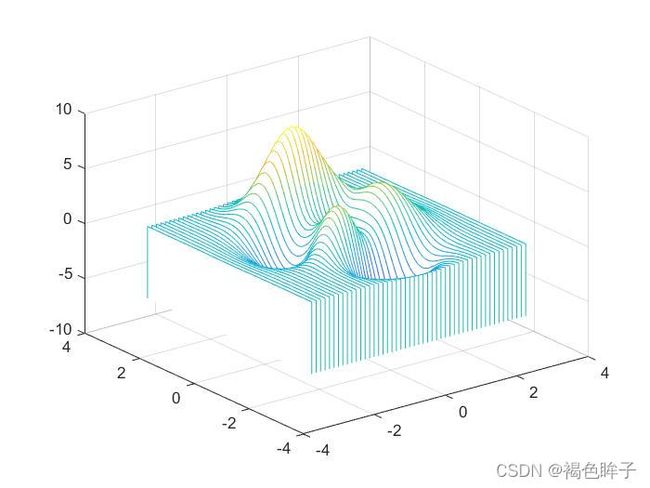
>> [x,y,z]=peaks;
>> waterfall(x',y',z');