【算法】原地哈希与快速幂

一、原地哈希

直接看例题：题目链接
题目描述：
给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

示例 1：

输入：nums = [1,2,0]
输出：3

示例 2：

输入：nums = [3,4,-1,1]
输出：2

示例 3：

输入：nums = [7,8,9,11,12]
输出：1

思路分析：
拿到这道题如果没有限制条件很容易想到两种方法，第一种就是哈希表+遍历，第二种是排序+遍历，但是第一种方法空间复杂度超限，第二种时间复杂度超限。
而这里就可以用原地哈希来做。
假设数组的长度为N，那么我们要找的数一定会在1 ~ N+1之间，因为数组的下标是0 ~ N，所以我们可以把当前数组当场哈希表。
具体实现：

把数字1放到下标为0的位置，把数字2放到下标1的位置，以此类推。也就是把数值为i的数映射到i - 1的位置。
当遍历到指定位置的时候，就把当前位置的数字放到指定位置，把指定位置的数字替换回来，重复操作，知道nums[i] == i + 1，这样遍历到后边的位置如果符合条件直接跳过。时间复杂度为O(N)。

class Solution {
public:
    int firstMissingPositive(vector<int>& nums) {
        int n = nums.size();
        for(int i = 0; i < n; i++)
        {
            while(nums[i] != i + 1)
            {
                if(nums[i] <= 0 || nums[i] > n || nums[i] == nums[nums[i] - 1])
                {
                    break;
                }
                int idx = nums[i] - 1;
                swap(nums[idx], nums[i]);
            }
        }
        for(int i = 0; i < n; i++)
        {
            if(nums[i] != i + 1)
            {
                return i + 1;
            }
        }
        return n + 1;
    }
};

二、快速幂

2.1 指数无负数

快速幂主要解决的是a^b % p的场景，如果正常算的话需要循环b次来计算。但是这是可以优化的：

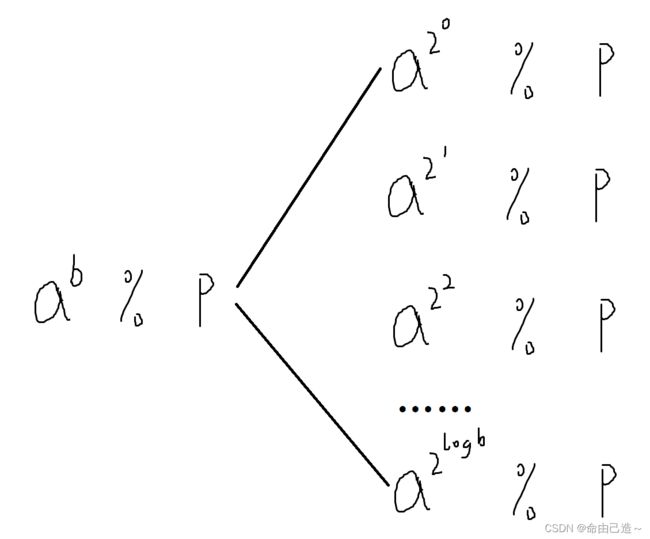
可以看到每个数都是上一个数的平方 % p

先不看取模，我们现在要求a^b，其实就是从这些数字里平凑出来。

举个例子，现在要求3^5：
5的二进制表示为0101：

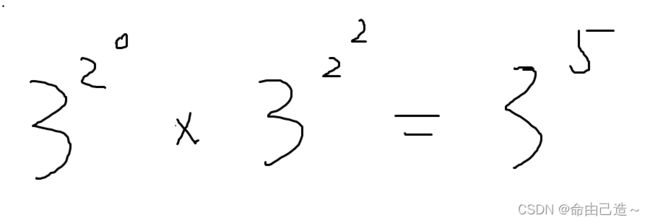
那么我们就可以循环b，当b & 1 != 0，结果就要乘上a，每次把b右移1，并且把a的值平方。

看一道例题：
题目链接

题目描述：

输入格式

第一行包含整数 n。
接下来 n 行，每行包含三个整数 ai,bi,pi。

输出格式

数据范围

1≤n≤100000,1≤ai,bi,pi≤2×109

输入样例：

2
3 2 5
4 3 9

输出样例：

4
1

#include 

using namespace std;

long long qmi(int a, int b, int p)
{
    long long res = 1;
    while(b)
    {
        if(b & 1)
        {
            res = (long long)res * a % p;
        }
        b >>= 1;
        // 每个数是上一个数的平方 % p
        a = (long long)a * a % p;
    }
    return res;
}

int main()
{
    int n;
    scanf("%d", &n);
    while(n--)
    {
        int a, b, p;
        scanf("%d %d %d", &a, &b, &p);
        printf("%d\n", qmi(a, b, p));
    }
    return 0;
}

2.2 指数有负数

上面的指数都是整数，而如果指数含有负数呢？
当b < 0 的时候，只需要做两步即可：
1️⃣ 把a变成 1 / a
2️⃣ 把b变成-b

但是这里要注意当b是-2^31，直接转化成整数会导致越界，所以可以用一个long long型的变量临时存储。

class Solution {
public:
    double myPow(double x, int n) {
        double res = 1;
        long long b = n;
        if(b < 0)
        {
            x = 1 / x;
            b = -b;
        }
        while(b)
        {
            if(b & 1)
            {
                res = res * x;
            }
            b >>= 1;
            x = x * x;
        }
        return res;
    }
};

---

---