LeetCode刷题笔记

 

目录

 1177.构建回文串检测

剑指Offer 42.连续数组的最大和

 112.路径总和

---

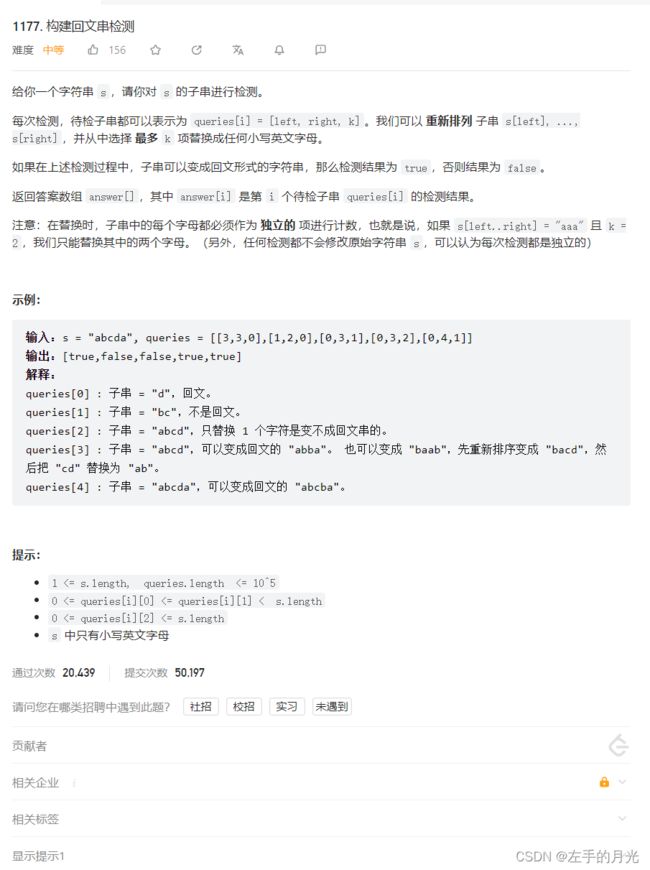
 1177.构建回文串检测

        首先我们要明白，偶数个数的字母可以平均分布在两侧，因此统计奇数的个数即可，奇数个数的字母大于1时肯定不是回文数。但是题目个数可以任意变换k个字母，变换一个字母可以至多使两个字母数量变为偶数，因此统计奇数字母的个数。大于k*2+1时不能变为回文字串。

        那怎么子串统计奇数字母的数量呢？我们利用前缀和，一个二维数组。数组有26列，代表26个字母的个数，数组第i行代表字符串前i个字母，每个字母的个数。那么当求[left,right]字串每个字母分别的个数时。只需相减即可（注意right要包括，因此要加一）。

class Solution {
public:
    vector canMakePaliQueries(string s, vector>& queries) {
        int len=s.size();   //字符串总共的长度
        vector>  SUM_ZI(len+1,vector(26,0));   //建立二维数组
        for(int i=1;i<=len;i++){                                //遍历整个字符串
            SUM_ZI[i]=SUM_ZI[i-1];                              //后一行继承前一行的状态
            SUM_ZI[i][s[i-1]-'a']++;                           
                                                           //查看当前是哪一个字母，加进去
        }
        vector g;
        for(auto& meige:queries){
            int left=meige[0],right=meige[1],k=meige[2],sum=0;
            for(int i=0;i<26;i++){
                sum+=(SUM_ZI[right+1][i]-SUM_ZI[left][i])&1;
            }
            g.emplace_back(!(sum>(k*2+1)));
        }
        return g;
    }
};

 优化：

        其实我们不需要求出子串每个字母的数量，我们只需要判断奇偶型即可。两种状态，很容易联想到状态压缩。我们设置一个一维数组(SUM_ZI)优化二维数组。首先26个字母，我们使用unsigned int，其有32位，每位有0和1两种状态，我们把1看做奇数，0看做偶数。从右向左分别代表a到z字母，只需要26位即可。

        那我们怎么改变其奇偶状态呢？我们用^运算符，首先我们计算要在哪一位改变。即字符串是哪一个字母，然后异或改变即可。SUM_ZI[i]=SUM_ZI[i-1]^(1<<(s[i-1]-'a')); 那现在要求子串的状态怎忙办？你想一下，右边界'a'有偶数个，左边界也有偶数个，那么字串一定是偶数个或者0，奇数也是如此。只有一奇一偶时才字串才是奇数，那么只需SUM_ZI[right+1]^SUM_ZI[left]，位数为1代表该字串某字母个数为奇数，然后统计1的个数和k*2+1做比较即可。优化完成。

class Solution {
public:
    vector canMakePaliQueries(string s, vector>& queries) {
        int len=s.size();                           //字符串总共的长度
        vector SUM_ZI(len+1,0);                 //建立一个数组
        for(int i=1;i<=len;i++){                     //遍历整个字符串
            SUM_ZI[i]=SUM_ZI[i-1]^(1<<(s[i-1]-'a')); //标记是否是奇数，1为奇数
            
        }
        vector g;
        for(auto& meige:queries){                    //遍历容器
            int left=meige[0],right=meige[1],k=meige[2];
            unsigned int sum=__builtin_popcount(SUM_ZI[right+1]^SUM_ZI[left]);
            g.emplace_back(!(sum>(k*2+1)));
        }
        return g;
    }
    
};

 

 __builtin_popcount：__builtin_popcount()是 GCC 编译器的内置函数。它可以返回输入数据中，无符号二进制中‘1’的个数。

 

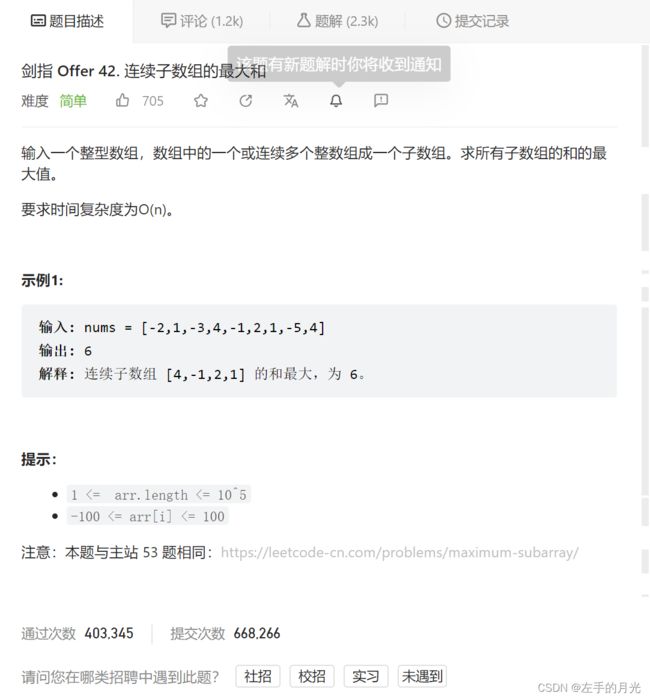
剑指Offer 42.连续数组的最大和

 

动态规划：建立dp[i]数组，dp[i]代表以下标为i结尾时数组的最大和。其有两种状态：

nums[i]>0:  dp[i]=dp[i-1]+nums[i]

nums[i]<0:  dp[i]=nums[i]

两种状态取最大值，就是以i为下标结尾的数组最大值，取dp数组的最大值就是该题答案；

class Solution {
public:
    int maxSubArray(vector& nums) {
        int len=nums.size();
        int* dp = new int[len];
        dp[0]=nums[0];
        int Max=nums[0];
        for(int i=1;i

 优化：利用滚动数组优化，空间复杂度为O(1);

class Solution {
public:
    int maxSubArray(vector& nums) {
        int len=nums.size();
        int dp = nums[0];
        int Max=nums[0];
        for(int i=1;i

 

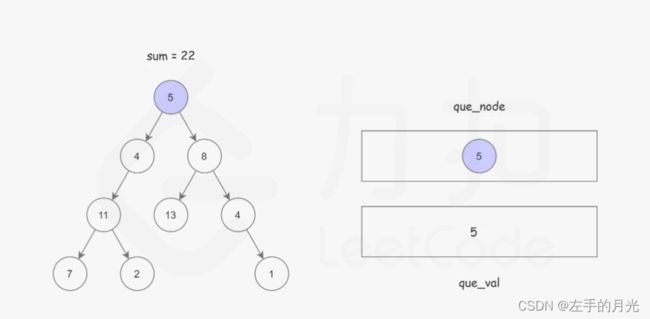
 112.路径总和

 

BFS：首先该结构是二叉树，采用链表存储，我们利用BFS，建立两个队列，一个队列存储节点路径，另一个队列存储该路径的和；

 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root==nullptr){
            return false;
        }
        queue tree;   
        queue sum_val;
        tree.push(root);
        sum_val.push(root->val);
        while(!tree.empty()){
            TreeNode* first=tree.front();
            int sum=sum_val.front();
            tree.pop();
            sum_val.pop();
            if(first->left==nullptr&&first->right==nullptr){
                if(sum==targetSum){
                    return true;
                }
                continue;
            }
            if(first->right!=nullptr){
                tree.push(first->right);
                sum_val.push(sum+first->right->val);
            }
            if(first->left!=nullptr){
                tree.push(first->left);
                sum_val.push(first->left->val+sum);
            }

        }
        
        return false;
    }
};

递归：

假定从根节点到当前节点的值之和为 val，我们可以将这个大问题转化为一个小问题：是否存在从当前节点的子节点到叶子的路径，满足其路径和为 val。

不难发现这满足递归的性质，若当前节点就是叶子节点，那么我们直接判断 sum 是否等于 val 即可（因为路径和已经确定，就是当前节点的值，我们只需要判断该路径和是否满足条件）。若当前节点不是叶子节点，我们只需要递归地询问它的子节点是否能满足条件即可，很像DFS；

class Solution {
public:
    bool  hasPathSum(TreeNode* root, int targetSum) {
        if(root==nullptr){
            return false;
        }
        if(root->left==nullptr&&root->right==nullptr){
            return  targetSum==root->val;
        }
        return  hasPathSum(root->left, targetSum-root->val) ||
                hasPathSum(root->right, targetSum-root->val);

    }
};

 ||用的很妙，只要一个返回值为true，那么返回值都变为true。