面试之类别数据处理（one-hot、embedding）

场景描述

类别型特征（Categorical Feature）是指反映（事物）类别的数据，是离散数据，其数值个数（分类属性）有限（但可能很多），比如性别（男、女）、血型（A、B、AB、O）等只在有限选项内取值的特征。类别型特征原始输入通常是字符串形式，除了决策树等少数模型能直接处理字符串形式的输入，对于逻辑回归、支持向量机等模型来说，类别型特征必须经过处理转换成数值型特征才能正确工作。

（连续变量：在一定区间内可以任意取值的变量叫连续变量,其数值是连续不断的,相邻两个数值可作无限分割,即可取无限个数值，如身高可以是183，也可以是183.1，也可以是183.111……；离散变量是指其数值只能用自然数或整数单位计算的则为离散变量, 例如，职工个数(总不能是1.2个吧)）

1、标签/序号编码（Ordinal Encoding）

序号编码通常用于处理类别间具有大小关系的数据。例如成绩，可以分为低、中、高三档，并且存在“高>中>低”的排序关系。序号编码会按照大小关系对类别型特征赋予一个数值ID，例如高表示为3、中表示为2、低表示为1，转换后依然保留了大小关系。**对于不具有大小关系的类别数据不建议使用。**对于基于非线性树的算法很有用（仅限于lightgbm和catboost这类可以直接处理类别的算法，xgboost还是要进行别的处理）在python中sklearn可以调用，from sklearn.preprocessing
import LabelEncoder。

2、独热编码（One-Hot Encoding）

独热编码通常用于处理类别间不具有大小关系的特征。例如血型，一共有4个取值（A型血、B型血、AB型血、O型血），独热编码会把血型变成一个4维稀疏向量，A型血表示为（1, 0,0, 0），B型血表示为（0, 1, 0, 0），AB型表示为（0, 0,1, 0），O型血表示为（0, 0, 0, 1）。

在python中有pandas的get_dummies和sklearn（from sklearn.preprocessing import OneHotEncoder）（遗憾的是sklearn中的OneHotEncoder无法直接对字符串型的类别变量编码，可以对数值型编码；而get_dummies对列是字符型还是数字型都可以进行二值编码） 具体说明可参考：
https://blog.csdn.net/wl_ss/article/details/78508367

注意: get_dummies 不像 sklearn 的 transformer一样，有 transform方法，所以一旦测试集中出现了训练集未曾出现过的特征取值，简单地对测试集、训练集都用 get_dummies 方法将导致数据错误。

2.1 为什么要独热编码？

独热编码（哑变量 dummy variable）是因为大部分算法是基于向量空间中的度量来进行计算的，为了使非偏序关系的变量取值不具有偏序性，并且到圆点是等距的。使用one-hot编码，将离散特征的取值扩展到了欧式空间，离散特征的某个取值就对应欧式空间的某个点。将离散型特征使用one-hot编码，会让特征之间的距离计算更加合理。离散特征进行one-hot编码后，编码后的特征，其实每一维度的特征都可以看做是连续的特征。就可以跟对连续型特征的归一化方法一样，对每一维特征进行归一化。比如归一化到[-1,1]或归一化到均值为0,方差为1。

2.2 为什么特征向量要映射到欧式空间？

将离散特征通过one-hot编码映射到欧式空间，是因为，在回归、分类、聚类等机器学习算法中，特征之间距离的计算或相似度的计算是非常重要的，而我们常用的距离或相似度的计算都是在欧式空间的相似度计算，计算余弦相似性，基于的就是欧式空间。

2.3 独热编码优缺点

• 优点：解决了分类器不好处理数据属性的问题，在一定程度上也起到了扩充特征的作用。它的值只有0和1，不同的类型存储在垂直的空间。
• 缺点：在类别数量特别多的时候，会使得特征维度变得特别大，造成维数灾难。解决办法一般是使用PCA主成分分析来减少维度。

对于类别取值较多的情况下使用独热编码需要注意以下问题。
（1）使用稀疏向量来节省空间。在独热编码下，特征向量只有某一维取值为1，其他位置取值均为0。因此可以利用向量的稀疏表示有效地节省空间，并且目前大部分的算法均接受稀疏向量形式的输入。
（2）配合特征选择来降低维度。高维度特征会带来几方面的问题。一是在K近邻算法中，高维空间下两点之间的距离很难得到有效的衡量；二是在逻辑回归模型中，参数的数量会随着维度的增高而增加，容易引起过拟合问题；三是通常只有部分维度是对分类、预测有帮助，因此可以考虑配合特征选择来降低维度。

2.4 什么情况下(不)用独热编码？

• 用：独热编码用来解决类别型数据的离散值问题
• 不用：将离散型特征进行one-hot编码的作用，是为了让距离计算更合理，但如果特征是离散的，并且不用one-hot编码就可以很合理的计算出距离，那么就没必要进行one-hot编码。 有些基于树的算法在处理变量时，并不是基于向量空间度量，数值只是个类别符号，即没有偏序关系，所以不用进行独热编码。Tree Model不太需要one-hot编码： 对于决策树来说，one-hot的本质是增加树的深度。

总的来说，要是one hot encoding的类别数目不太多，建议优先考虑。

2.5 虚拟变量陷阱

2.5.1 虚拟变量

如何对非定量因素进行回归分析？直接在回归模型中加入定性因素（比如类别因素：男或女）存在困难，因此可以考虑把定性因素量化，使定性因素与定量因素在回归模型中起到相同的作用。这时就用到了虚拟变量。
计量经济学中，把取值为0或者1的变量称为虚拟变量（或哑元变量）。例如用0表示女、1表示男。这样就把定性因素进行了量化。从理论上讲，虚拟变量取“0”通常代表比较的基础类型（也就是基期/参照物）；而虚拟变量取“1”通常代表被比较的类型（即报告期）。

虚拟变量数量的设置规则：

• 若定性因素具有m个（m>1）相互排斥属性，并且回归模型有截距项时，只能引入m-1个虚拟变量，否则，就会陷入“虚拟变量陷阱”
• 当回归模型无截距项时，则可引入m个虚拟变量。

虚拟变量的解释看下述链接中前12页：
https://wenku.baidu.com/view/7265e32126284b73f242336c1eb91a37f11132f9.html

2.5.2 虚拟变量陷阱

虚拟变量陷阱的实质：完全多重共线性。

多重共线性指自变量间存在线性相关关系，即一个自变量可以用其他一个或几个自变量的线性表达式进行表示。若存在多重共线性，计算自变量的偏回归系数B=[(X‘X)-1]X’Y时，矩阵(X’X)不可逆，导致B存在无穷多个解或无解。实际分析中模型主要有以下几种表现：
1、整个模型的检验结果为$P<\alpha$，但各自变量的偏回归系数的统计学检验结果却是$P>\alpha$.
2、专业上认为应该有统计学意义的自变量检验结果却无统计学意义。
3、自变量的偏回归系数取值大小甚至符号明显与实际情况相违背，难以解释。
4、增加或删除一个自变量或一条记录，自变量片回归系数发生较大变化。

虚拟变量陷阱（Dummy Variable Trap）：指当原特征有m个类别时，如果将其转换成m个虚拟变量，就会导致变量间出现完全共线性的情况，也就是一个变量可以被其他变量推导出。

举个例子：对于定性因素性别而言，它有两个水平——男和女，可以用一个虚拟变量x表示（类似与标签编码），x=1表示男，x=0表示女；也可以用两个虚拟变量x和y表示（实际上就是one-hot编码），x=1表示是男，x=0表示不是男，同理y=1表示女，y=0表示不是女。通过one-hot会建立线性回归模型如下：
$$y=b+\{0\mid 1\}male+\{0\mid 1\}female$$

对应的矩阵格式如下：

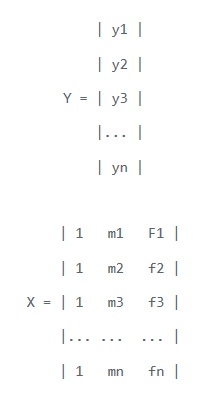
在上述模型中，每一行所有类别虚拟变量的总和等于该行的截距值。换句话说，存在完美的多重共线性（可以从其他值中预测一个值）。直观地讲，存在一个重复的类别：如果我们删除了男性类别，则其固有地在女性类别中定义（零女性值表示男性，反之亦然）。

虚拟变量陷阱的解决方案是删除分类变量之一（或删除截距常量）。如果存在m个类别，则在模型中使用m-1。

举个例子，一个包含3个类别的变量，C1、C2和C3。如下：

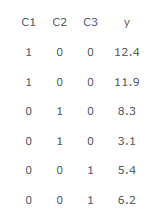
在有截距项b时，回归模型为 $y=a1\times C1+a2\times C2+a3\times C3+b$。按上图中的虚拟变量设置，用OLS（ordinary least squares）求解方程的时候，模型解为
$$B=(X^{T}X{)}^{-1}{X}^{T}Y$$

当有截距项b的并用时候，用上述公式求解模型（也就是解析解）就会遇到“虚拟变量陷阱”。矩阵X’X是不可逆的，是一个奇异矩阵（非满秩）。此时，有两种办法避免“虚拟变量陷阱”：去掉截距项b或者减少一个虚拟变量。

2.5.3 小结

可以看到所谓“虚拟变量陷阱”的原因是：多重共线性导致OLS算法中矩阵不可逆。从而无法计算回归模型的系数。
“虚拟变量陷阱”是和回归模型的求解算法有关的，上述的OLS的闭式解会报错，但是可能用其他求解算法（比如梯度下降）还可以计算。

若定性因素有m个互相排斥的属性（例如定性因素“性别”有m=2个相互排斥的属性:男和女）：

• 当回归模型有截距项时，只能引入m-1个虚拟变量，否则就会陷入“虚拟变量陷阱”；
• 当回归模型无截距项时，可以引入m个虚拟变量。

上述数据如果用Python的sklearn.linear_model.LinearRegression（默认是有截距项b的），X={C1,C2,C3}，Y={y}，是不会报错的。但是用R中的线性回归函数lm时（参数也是X={C1,C2,C3}，Y={y}）计算出的一个系数是NA。在python中若想避免共线性也是可以的，pd.get_dummies中有参数可以达到这个目的（删除第一列），其实就是用全0来表示一种类别其它都用1-0表示。

需要注意的是，针对二元定性变量到虚拟变量的转换，直接对类别进行数字编码（男：0，女：1）和将其转换为虚拟变量（男：[0]，女：[1]）看似一样，但这只是一个巧合而已，这两种方法有本质的区别。前者是直接将类别型变量转变成离散值进行表示，后者是减少一个变量（作为基准），只留取一个变量，在此基础上对另一个变量进行推论。一定要注意不要搞混了。

**还有一点需要注意的是，基准类别该如何选择？**如果基准类别选择不合理，虚拟变量之间仍然会存在共线性的问题。这里直接给出结论：选择占比最大的类别作为基准类别。假设有a，b，c三个类别，如果基准类别a占比太少，那么即使把a去除，b和c之和也会接近于1，还是会有很强的共线性。

3、二进制编码（Binary Encoding）

二进制编码主要分为两步，先用序号编码给每个类别赋予一个类别ID，然后将类别ID对应的二进制编码作为结果。以A、B、AB、O血型为例，表1.1是二进制编码的过程。A型血的ID为1，二进制表示为001；B型血的ID为2，二进制表示为010；以此类推可以得到AB型血和O型血的二进制表示。可以看出，二进制编码本质上是利用二进制对ID进行哈希映射，最终得到0/1特征向量，且维数少于独热编码，节省了存储空间。Python的sklearn中有相关的函数。

4、embedding

对于类别特征的处理，最常见的思路是转为one-hot编码，当然这种处理方式比较粗暴，在许多算法里效果也不是很好。当类别很多时，独热编码（One-hot encoding）向量是高维且稀疏的，大数据集下这种方法的计算效率是很低的。

Embedding的起源和火爆都是在NLP中的，经典的word2vec都是在做word embedding这件事情，而真正首先在结构数据探索embedding的是在kaggle上的《Rossmann Store Sales》中的rank 3的解决方案，作者在比赛完后为此方法整理一篇论文放在了arXiv，文章名：《Entity Embeddings of Categorical
Variables》。其网络结构如下图所示：

结构非常简单，就是embedding层后面接上了两个全连接层，代码用keras写的，构建模型的代码量也非常少，用的keras的sequence model。文章的代码地址：https://github.com/entron/entity-embedding-rossmann。
使用嵌入后的向量可以提高其他算法（KNN、随机森林、gdbt）的准确性。

因此，如果我们对类别特征做embedding之后，拿到embedding后的特征后，就可以放到其它的一些学习器中进行训练，并且效果在诸多比赛中得到了验证，所以说这是一种处理类别特征的方法。

利用神经网络中的embedding层得到的结果，来作为原来类别特征的替换，然后用于训练其它模型。Keras文档里是这么写embedding的：“把正整数（索引）转换为固定大小的稠密向量”。下面举例说明Embedding的过程：

以性别、星期、居住城市、这3个类别特征为例，它们需要经过如下步骤：

• 步骤一：分别做one-hot编码，即 Gender=Male∈​{男、女}表示成[1,0]，week=Wednesday表示成[0, 0, 1, 0, 0, 0, 0]，City=Zhengzhou​∈​{北京、深圳、郑州} 表示成[0, 0，1]；

• 步骤二：将所有的one-hot编码特征首尾相连，构成新的输入向量x=[1,0,0,0,1,0,0,0,0,0,0,1]​

• 步骤三：将输入向量和权重做矩阵乘法运算，得到当前网络层的输出；

图像化表示如下，

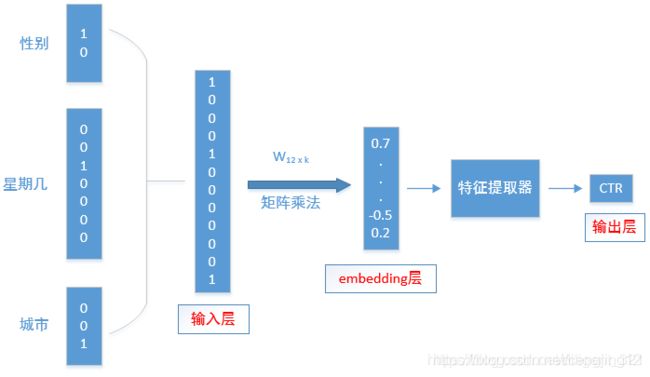
注意：上图中的embedding层等价于，先将输入的三个类别特征分别求取embedding向量形式，然后将embedding向量逐像素求和。其中的权重矩阵$W_{12}\ast k$就是embedding特征，k是embedding向量的维度，可自行设置。$W_{12}\ast k$其中的前两行对应着性别的embedding特征，第3-9行向量对应着7个星期，后3个对应着城市的embedding特征。

通过embedding的方式就可以将类别变量转换成一个k维的向量来表述，与直接用one-hot相比，维度降低，而且对模型的效果也比直接使用one-hot要好。可以使用keras中的Embedding来直接实现。实现示例可参考下面两篇文章：
利用神经网络的embedding层处理类别特征
一文搞懂word embeddding和keras中的embedding

5 计数编码（频率编码Count编码）

• 将类别特征替换为训练集中的计数（一般是根据训练集来进行计数，属于统计编码的一种，统计编码，就是用类别的统计特征来代替原始类别，比如类别A在训练集中出现了100次则编码为100）
• 对线性和非线性算法均有用
• 可能对异常值敏感
• 可以添加对数转换，可以很好地处理计数（主要是针对count编码之后特征分布不规则的问题和常规的处理不规则分布的连续特征是一样的方式）
• 用’1’替换新数据中没见过的类别（没见过的类别如果有n个则编码为n）
• 可能会产生冲突：相同的编码，不同的变量（不同类别出现次数一样）

6 树模型自动处理类别变量

• XgBoost和Random Forest，不能直接处理categorical feature，必须先编码成为numerical feature。

• lightgbm和CatBoost，可以直接处理categorical feature。

• lightgbm： 需要先做label encoding。用特定算法（On Grouping for Maximum
  Homogeneity）找到optimal split，效果优于ONE。也可以选择采用one-hot encoding。

• CatBoost： 不需要先做label encoding。可以选择采用one-hot encoding，target encoding (with regularization)。

7 目标编码（target encoding）

• 按目标变量的比例对分类变量进行编码（二分类或回归）（如果是多分类其实也可以编码，例如类别A对应的标签1有100个，标签2有100个，标签3有100个，则可以编码为【1/3,1/3,1/3】）

• 注意避免过拟合！（原始的target encoding直接对全部的训练集数据和标签进行编码，会导致得到的编码结果太过依赖与训练集）

• 堆叠形式：输出平均的目标的单变量模型

• 以交叉验证的方式进行（一般会进行交叉验证，比如划分为10折，每次对9折进行标签编码然后用得到的标签编码模型预测第10折的特征得到结果，其实就是常说的均值编码）

• 添加平滑以避免将变量编码设置为0。（某些类别可能只包含部分的类别会出现0值，此时会进行拉普拉斯平滑，不过对于回归则没有这种问题）

• 添加随机噪声以应对过拟合

• 正确应用时：线性和非线性的最佳编码

除了本章介绍的编码方法外，有兴趣的读者还可以进一步了解其他的编码方式，比如HelmertContrast、Sum Contrast、PolynomialContrast、Backward Difference Contrast等。

参考文章

参考1：https://blog.csdn.net/qq_41940950/article/details/102702689
参考2：https://blog.csdn.net/qq_36810398/article/details/101104360?utm_medium=distribute.pc_relevant.none-task-blog-baidujs-1
参考3：https://www.algosome.com/articles/dummy-variable-trap-regression.html