智能优化算法:浣熊优化算法-附代码
智能优化算法:浣熊优化算法
文章目录
- 智能优化算法:浣熊优化算法
-
- 1.浣熊优化算法
-
- 1.1 初始化
- 1.2 阶段一:狩猎和攻击(探索阶段)
- 2.实验结果
- 3.参考文献
- 4. Matlab
- 5.python
摘要:浣熊优化算法(Coati Optimization Algorithm(COA)),是于2022年提出的一种基于浣熊行为的优化算法,该算法通过模拟浣熊猎食行为来进行寻优,具有寻优能力强,收敛速度快等特点
1.浣熊优化算法
1.1 初始化
与其他优化算法类似,在寻优空间里随机初始化种群:
x i , j = l b j + r ⋅ ( u b j − l b j ) (2) x_{i, j}=l b_j+r \cdot\left(u b_j-l b_j\right) \tag{2} xi,j=lbj+r⋅(ubj−lbj)(2)
其中 x i , j x_{i,j} xi,j为个体, l b j lb_j lbj为寻优下边界, u b j ub_j ubj为寻优上边界, r r r为[0,1]之间的随机数。
1.2 阶段一:狩猎和攻击(探索阶段)
在搜索空间中更新coatis种群的第一阶段是基于模拟它们攻击鬣蜥(Iguana)时的策略进行建模的。在这一策略中,一群coatis爬上树去够一只鬣蜥并吓唬它。其他几只coatis在树下等待,直到鬣蜥摔倒在地。鬣蜥落地后,coatis攻击并猎杀它。这种策略导致coatis移动到搜索空间的不同位置,这表明了COA在解决问题空间的全局搜索中的探索能力。
在COA设计中,假设种群中最好成员的位置是鬣蜥的位置。也有人假设,一半的鬣蜥爬上树,另一半等待鬣蜥掉到地上。因此,使用等式(4)对从树上升起的涂层的位置进行数学模拟。
X i P 1 : x i , j P 1 = x i , j + r ⋅ ( Iguana j − I ⋅ x i , j ) , for i = 1 , 2 , … , ⌊ N 2 ⌋ a n d j = 1 , 2 , … , m . (4) X_i^{P 1}: x_{i, j}^{P 1}=x_{i, j}+r \cdot\left(\text { Iguana }_j-I \cdot x_{i, j}\right), \text { for } i=1,2, \ldots,\left\lfloor\frac{N}{2}\right\rfloor \\and j=1,2, \ldots, m. \tag{4} XiP1:xi,jP1=xi,j+r⋅( Iguana j−I⋅xi,j), for i=1,2,…,⌊2N⌋andj=1,2,…,m.(4)
鬣蜥摔倒在地后,它被放置在搜索空间中的一个随机位置。基于这个随机位置,地面上的涂层在搜索空间中移动,这是使用等式(5)和(6)模拟的。
Iguana G : Iguana a j G = l b j + r ⋅ ( u b j − l b j ) , j = 1 , 2 , … , m , (5) \begin{aligned} & \text { Iguana }^G: \text { Iguana } a_j^G=l b_j+r \cdot\left(u b_j-l b_j\right), j=1,2, \ldots, m \text {, } \end{aligned}\tag{5} Iguana G: Iguana ajG=lbj+r⋅(ubj−lbj),j=1,2,…,m, (5)
X i p 1 : x i , j P 1 = { x i , j + r ⋅ ( Iguana j j G − I ⋅ x i , j ) , F Iguana G < F i , x i , j + r ⋅ ( x i , j − Iguana j G ) , else, for i = ⌊ N 2 ⌋ + 1 , ⌊ N 2 ⌋ + 2 , … , N and j = 1 , 2 , … , m . (6) \begin{aligned} & X_i^{p 1}: x_{i, j}^{P 1}=\left\{\begin{array}{cl} x_{i, j}+r \cdot\left(\text { Iguana } j_j^G-I \cdot x_{i, j}\right), & F_{\text {Iguana }}^G
如果更新后的个体更优则更新当前个体,否则保持原状:
X i = { X i P 1 , F i P 1 < F i X i , else. (7) X_i=\left\{\begin{aligned} X_i^{P 1}, & F_i^{P 1}
这里 X i P 1 X_i^{P1} XiP1是更新后的新位置, I g u a n a Iguana Iguana为猎物鬣蜥的位置, r r r为[0,1]之间的随机数。I为随机选择的1或者2。
1.3 阶段二:逃离捕食者(开发阶段)
更新coatis在搜索空间中的位置的过程的第二阶段是基于coatis遇到捕食者和逃离捕食者时的自然行为进行数学建模的。当捕食者攻击一只coatis时,它会从自己的位置逃跑。Coati在这一战略中的举措使其处于接近当前位置的安全位置,这表明了COA在本地搜索中的局部搜索能力。
为了模拟这种行为,基于等式(8)和(9),在每个coatis所在的位置附近生成随机位置。
l b j local = l b j t , u b j local = u b j t , where t = 1 , 2 , … , T (8) \begin{gathered} l b_j^{\text {local }}=\frac{l b_j}{t}, u b_j^{\text {local }}=\frac{u b_j}{t}, \text { where } t=1,2, \ldots, T \end{gathered}\tag{8} lbjlocal =tlbj,ubjlocal =tubj, where t=1,2,…,T(8)
X i P 2 : x i , j P 2 = x i , j + ( 1 − 2 r ) ⋅ ( l b j local + r ⋅ ( u b j local − l b j local ) ) , i = 1 , 2 , … , N , j = 1 , 2 , … , m (9) \begin{gathered} X_i^{P 2}: x_{i, j}^{P 2}=x_{i, j}+(1-2 r) \cdot\left(l b_j^{\text {local }}+r \cdot\left(u b_j^{\text {local }}-l b_j^{\text {local }}\right)\right), \\ i=1,2, \ldots, N, j=1,2, \ldots, m \end{gathered}\tag{9} XiP2:xi,jP2=xi,j+(1−2r)⋅(lbjlocal +r⋅(ubjlocal −lbjlocal )),i=1,2,…,N,j=1,2,…,m(9)
其中t 为迭代次数,如果更新后的个体更优则更新当前个体,否则保持原状:
X i = { X i P 2 , F i P 2 < F i X i , else (10) X_i=\left\{\begin{aligned} X_i^{P 2}, & F_i^{P 2}
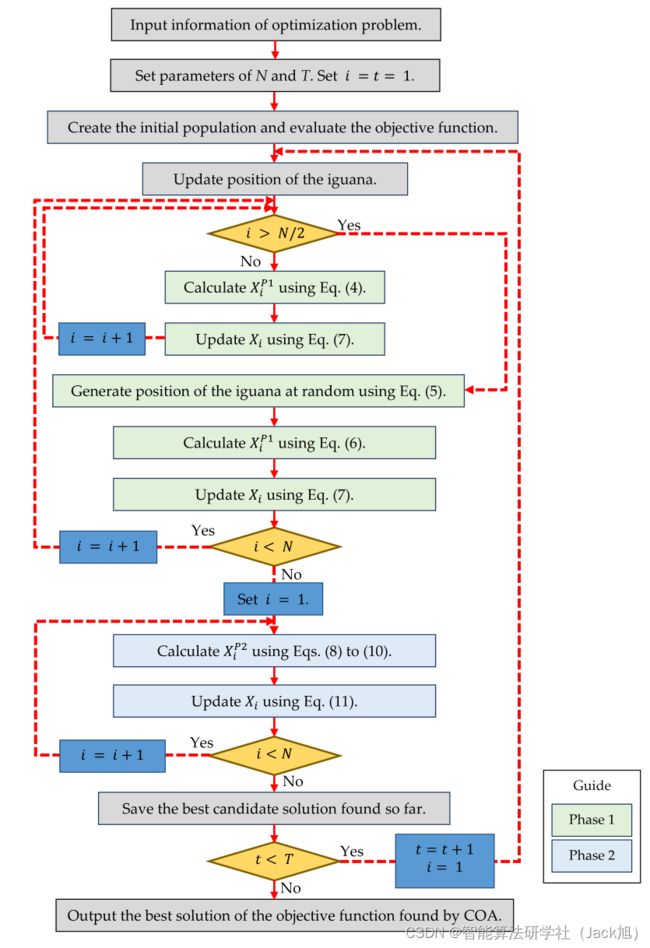
算法流程图如下:
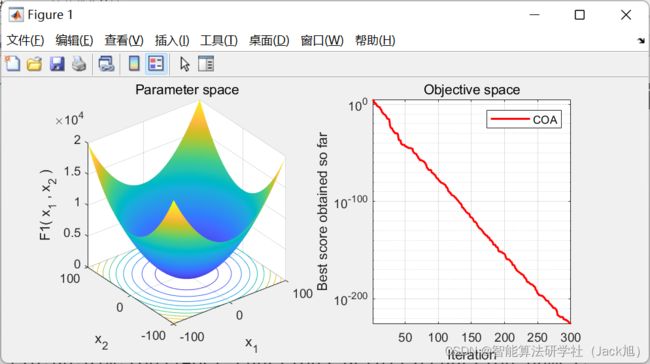
2.实验结果
3.参考文献
[1]Dehghani Mohammad,Montazeri Zeinab,Trojovská Eva,Trojovský Pavel. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems[J]. Knowledge-Based Systems,2023,259.
uristic algorithm for solving optimization problems[J]. Knowledge-Based Systems,2023,259.