【图神经网络】图神经网络(GNN)学习笔记:Graph Embedding
图神经网络(GNN)学习笔记:Graph Embedding
- 为什么要进行图嵌入Graph embedding?
- Graph Embedding
- 使用图嵌入的优势有哪些?
- 图嵌入的方法有哪些?
-
- 节点嵌入方法(Node Embeddings)
-
- 1. DeepWalk
- 2. LINE
-
- 一阶相似度
- 二阶相似度
- 优化目标
- 优化技巧
- 示例代码
- 3. SDNE
- 4. Node2vec
- 5. Struc2vec
- 图嵌入方法
-
- 1. Graph2vec
- 其他的方法
- 总结
- 相关资料
Graph广泛存在于真实世界的多种场景中,即节点和边的集合。比如社交网络中人与人之间的联系,生物中蛋白质相互作用以及通信网络中的IP地址之间的通信等等。除此之外,我们最常见的一张图片、一个句子也可以抽象地看做是一个图模型的结构,图结构可以说是无处不在。
对于Graph的研究可以解决下面的一些问题:比如社交网络中新的关系的预测,在QQ上看到的推荐的可能认识的人;生物分子中蛋白质功能、相互作用的预测;通信网络中,异常事件的预测和监控以及网络流量的预测。如果要解决以上的问题,我们首先需要做的是对图进行表示,graph embedding 是中非常有效的技术。
为什么要进行图嵌入Graph embedding?
图嵌入(Graph Embedding)在图数据分析和机器学习中具有重要的作用。以下是一些进行图嵌入的主要原因:
-
降维和可视化: 图数据通常是高维的,其中包含大量的节点和边。通过将图嵌入到低维空间中,可以将复杂的图结构转化为易于理解和可视化的形式,帮助我们直观地观察和分析图的特征和模式。
-
特征表示: 图嵌入可以将节点和边转换为连续向量表示,从而将图中的离散信息转化为可计算和可学习的特征表示。这使得我们可以将传统的机器学习和深度学习方法应用于图数据,并利用这些表示进行节点分类、链接预测、图聚类等任务。
-
相似性和关系建模: 图嵌入可以在嵌入空间中捕捉节点和边之间的相似性和关系。相似的节点在嵌入空间中会彼此靠近,而具有相似关系的边也会在嵌入空间中表现出相似的模式。这为基于相似性的推荐系统、社交网络分析、链接预测等任务提供了有力的工具。
-
信息传递和表示学习: 图嵌入可以通过考虑节点和边之间的邻近关系和传递信息来学习更丰富的节点表示。通过在嵌入过程中考虑图的拓扑结构,嵌入模型可以捕捉到节点在图中的位置和周围的上下文,从而提供更丰富和准确的节点表示。
总而言之,图嵌入提供了一种将图数据转化为可计算和可学习的表示形式的方法,使我们能够利用机器学习和深度学习技术对图进行分析、挖掘和预测。它在许多领域中都具有广泛的应用,如社交网络分析、生物信息学、推荐系统、网络安全等。
Graph Embedding
图嵌入是一种将图数据(通常为高维稠密的矩阵)映射为低微稠密向量的过程,能够很好地解决图数据难以高效输入机器学习算法的问题。图嵌入需要捕捉到图的拓扑结构,顶点与顶点的关系,以及其他的信息,如子图,连边等。如果有更多的信息被表示出来,那么下游的任务将会获得更好的表现。嵌入的过程中有一种共识:向量空间中保持连接的节点彼此靠近。基于此,研究者提出了拉普拉斯特征映射(Laplacian Eigenmaps)和局部线性嵌入(Locally Linear Embedding ,LLE)。

总的来说大致可以将图上的嵌入分为两种:节点嵌入和图嵌入。当需要对节点进行分类,节点相似度预测,节点分布可视化,一般采用节点的嵌入;当需要在图级别上进行预测或者预测整个图结构,我们需要将整个图表示为一个向量。
后面将会介绍一下经典的方法如DeepWalk, node2vec, SDNE和graph2vec.
使用图嵌入的优势有哪些?
图是数据的有意义且易于理解的表示形式,但出于下面的原因需要对图进行嵌入表示。
- 在graph直接进行机器学习具有一定的局限性,我们都知道图是由节点和边构成的,这些向量关系一般只能使用数学,统计或者特定的子集进行表示,但是嵌入之后的向量空间具有更加灵活和丰富的计算方式;
- 图嵌入能够压缩数据, 我们一般用邻接矩阵描述图中节点之间的连接。连接矩阵的维度是 ∣ V ∣ x ∣ V ∣ |V| x |V| ∣V∣x∣V∣,其中 ∣ V ∣ |V| ∣V∣ 是图中节点的个数。矩阵中的每一列和每一行都代表一个节点。矩阵中的非零值表示两个节点已连接。将邻接矩阵用用大型图的特征空间几乎是不可能的。一个具有 1 M 1M 1M个节点和 1 M x 1 M 1Mx1M 1Mx1M的邻接矩阵的图该怎么计算和表示呢?但是嵌入可以看做是一种压缩技术,能够起到降维的作用;
- 向量计算比直接在图上操作更加的简单、快捷。
但是图嵌入也需要满足一定的需求
- 属性选择:确保嵌入能够很好地描述图的属性。它们需要表示图拓扑,节点连接和节点邻域。预测或可视化的性能取决于嵌入的质量;
- 可扩展性:大多数真实网络都很大,包含大量节点和边。嵌入方法应具有可扩展性,能够处理大型图。定义一个可扩展的模型具有挑战性,尤其是当该模型旨在保持网络的全局属性时。网络的大小不应降低嵌入过程的速度。一个好的嵌入方法不仅在小图上高效嵌入,同时也需要在大图上能够高效地嵌入;
- 嵌入的维度:实际嵌入时很难找到表示的最佳维数,维度越大能够保留的信息越多,但是通常有更高的时间和空间复杂度。较低的维度虽然时间、空间复杂度低,但无疑会损失很多图中原有的信息。
图嵌入的方法有哪些?
图嵌入(Graph Embedding)的方法有很多,以下是一些常见的图嵌入方法:
-
节点嵌入(Node Embedding):节点的嵌入借鉴了word2vec的方法,该方法能够成立的原因是:图中的节点和语料库中的单词的分布都遵循幂定律。
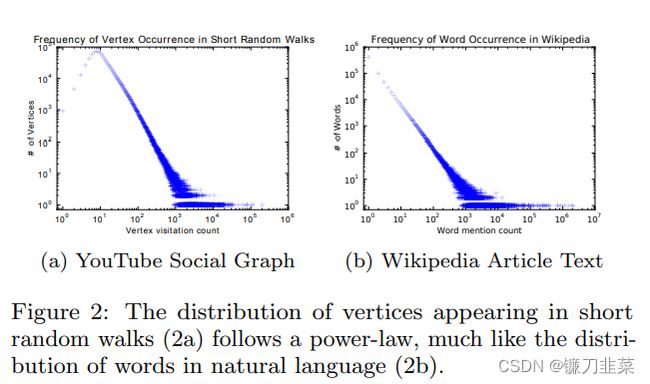
DeepWalk:利用随机游走采样图中的节点序列,然后使用Word2Vec模型将节点序列嵌入到低维向量空间中。node2vec:基于随机游走的节点采样策略,结合深度优先搜索和广度优先搜索来生成节点序列,然后使用Word2Vec进行嵌入学习。LINE:通过最大化邻居节点的相似性和最小化非邻居节点的相似性来学习节点嵌入。
-
图嵌入(Graph Embedding):
GraphSAGE:利用采样的邻居节点特征来学习节点的嵌入表示,通过聚合邻居节点的特征进行图嵌入学习。Graph Convolutional Network(GCN):通过卷积操作在图上进行特征传播,利用节点和邻居节点的特征来学习节点的嵌入表示。Graph Attention Network(GAT):利用自注意力机制来学习节点之间的关系,并根据节点的邻居节点特征进行嵌入学习。
-
子图嵌入(Subgraph Embedding):
GraphSAGE:通过采样和聚合子图的节点和边特征,学习子图的嵌入表示。Graph Isomorphism Networks(GIN):利用子图的局部结构信息,通过多层感知机进行子图嵌入学习。
-
图注意力网络(Graph Attention Network):
Graph Attention Network(GAT):通过利用自注意力机制来学习节点之间的关系,进而学习节点的嵌入表示。Graph Attention Graph Neural Network(GAGNN):扩展了GAT,通过学习节点和子图的注意力权重来进行嵌入学习。
-
随机游走嵌入(Random Walk Embedding):
DeepWalk:通过随机游走采样图中的节点序列,并利用Word2Vec模型将节点序列嵌入到低维向量空间中。Node2Vec:基于随机游走的节点采样策略,结合深度优先搜索和广度优先搜索来生成节点序列,然后利用Word2Vec进行嵌入学习。
这只是一小部分图嵌入方法的例子,还有其他许多方法和技术,如Graph Autoencoders、GraphGAN、GraphSNE等。每种方法都有其独特的特点和适用场景,选择适合特定任务和数据的图嵌入方法需要根据具体情况进行评估和选择。
补充一下NLP领域中的Word2Vec和Skip-gram模型:
- Word2vec是一种将单词转换为嵌入向量的嵌入方法。相似的词应具有相似的嵌入。Word2vec使用skip-gram网络,这是具有一层隐藏层的神经网络(总共三层)。skip-gram模型是给出某一词语来预测上下文相邻的单词。下图显示了输入单词(标有绿色)和预测单词的示例。通过此任务,作者实现了两个相似的词具有相似的嵌入,因为具有相似含义的两个词可能具有相似的邻域词。

图3 skip-gram模型。网络的输入为one-hot编码,长度与单词字典的长度相同,只有一个位置为1,输出为单词的嵌入表示.
下面介绍三个节点嵌入(node embedding)的方法,一个图嵌入(graph embedding)的方法,这些方法都类似Word2vec的嵌入原理。
节点嵌入方法(Node Embeddings)
下面介绍三种经典的节点嵌入的方法:DeepWalk, Node2vec, SDNE, LINE。
1. DeepWalk

DeepWalk通过随机游走(truncated random walk)学习出一个网络的表示,在网络标注顶点很少的情况也能得到比较好的效果。随机游走起始于选定的节点,然后从当前节点移至随机邻居,并执行一定的步数,该方法大致可分为三个步骤:
- 采样:通过随机游走对图上的节点进行采样,在给定的时间内得到一个节点构成的序列,论文研究表明从每个节点执行32到64次随机遍历就足够表示节点的结构关系;
- 训练skip-gram:随机游走与word2vec方法中的句子相当。文本中skip-gram的输入是一个句子,在这里输入为自随机游走采样得到了一个序列,进一步通过最大化预测相邻节点的概率进行预测。通常预测大约20个邻居节点——左侧10个节点,右侧10个节点;
- 计算嵌入:

DeepWalk通过随机游走去可以获图中点的局部上下文信息,因此学到的表示向量反映的是该点在图中的局部结构,两个点在图中共有的邻近点(或者高阶邻近点)越多,则对应的两个向量之间的距离就越短。但是DeepWalk方法随机执行随机游走,这意味着嵌入不能很好地保留节点的局部关系,Node2vec方法可以解决此问题。
DeepWalk 核心代码
DeepWalk算法主要包括两个步骤,第一步为随机游走采样节点序列,第二步为使用skip-gram modelword2vec学习表达向量。

①构建同构网络,从网络中的每个节点开始分别进行Random Walk 采样,得到局部相关联的训练数据; ②对采样数据进行SkipGram训练,将离散的网络节点表示成向量化,最大化节点共现,使用Hierarchical Softmax来做超大规模分类的分类器。

随机游走的核心代码如下:
import random
def randomwalk(G,gamma,t):
'''
:param G: 图结构,networks生成
:param gamma: 随机游走迭代轮数
:param t: 随机游走步数
:return: 返回游走序列
'''
W = [] #接收随机游走序列结果
for i in range(gamma):
node_list = list(G.nodes())
random.shuffle(node_list) #打乱节点集合顺序
for j in node_list:
w = [j]
v = j
while len(w) < t:
v_neig = list(G.neighbors(v)) #获取节点v所有邻居节点
w.append(random.choice(v_neig))
v = w[-1]
W.append(w)
return W
RandomWalk是一种可重复访问已访问节点的深度优先遍历算法。给定当前访问起始节点,从其邻居中随机采样节点作为下一个访问节点,重复此过程,直到访问序列长度满足预设条件。

其中第七步Skip-Gram具体算法为:

从算法流程看,已经访问过的节点还可以重复访问,所以是一种可重复访问已访问节点的深度优先遍历算法。其中,HS策略指的是Hierarchical Softmax
示例代码:
import random
from gensim.models import Word2Vec
import networkx as nx
# 构建图
G = nx.Graph()
G.add_edges_from([(1, 2), (1, 3), (2, 4), (2, 5), (3, 6), (3, 7), (4, 8), (4, 9)])
# 产生随机游走序列
def _simulate_walks(nodes, num_walks, walk_length):
walks = []
for _ in range(num_walks):
random.shuffle(nodes)
for v in nodes:
walks.append(deepwalk_walk(walk_length=walk_length, start_node=v))
return walks
# 从start_node开始随机游走
def deepwalk_walk(walk_length, start_node):
walk = [start_node]
while len(walk) < walk_length:
cur = walk[-1]
cur_nbrs = list(G.neighbors(cur))
if len(cur_nbrs) > 0:
walk.append(random.choice(cur_nbrs))
else:
break
return walk
# 每个节点进行随机游走的次数
num_walks = 10
# 每次随机游走的步数
walk_length = 5
# 得到所有节点
nodes = list(G.nodes())
# 随机游走生成节点序列
walks = _simulate_walks(nodes, num_walks=num_walks, walk_length=walk_length)
# 使用Word2Vec模型学习节点嵌入
model = Word2Vec(walks, vector_size=32, window=5, min_count=0, sg=1, workers=4, epochs=5)
# 获取节点的嵌入表示
node_embeddings = model.wv
# 打印节点的嵌入向量
for node in G.nodes():
print(f"Node {node}: {node_embeddings[node]}")
使用随机游走有两个好处:
- 并行化,随机游走是局部的,对于一个大的网络来说,可以同时在不同的顶点开始进行一定长度的随机游走,多个随机游走同时进行,可以减少采样的时间。
- 适应性,可以适应网络局部的变化。网络的演化通常是局部的点和边的变化,这样的变化只会对部分随机游走路径产生影响,因此在网络的演化过程中不需要每一次都重新计算整个网络的随机游走。
2. LINE
DeepWalk使用DFS随机游走在图中进行节点采样,使用word2vec在采样的序列学习图中节点的向量表示。LINE也是一种基于邻域相似假设的方法,只不过与DeepWalk使用DFS构造邻域不同的是,LINE可以看作是一种使用BFS构造邻域的算法。此外,LINE还可以应用在带权图中(DeepWalk仅能用于无权图)。

论文地址:https://arxiv.org/abs/1503.03578
LINE(Large-scale Information Network Embedding)是一种用于生成图嵌入的算法,旨在将图中的节点映射到低维向量空间。它通过最大化节点之间的邻居关系的概率来学习节点嵌入,以保持节点在低维空间中的相似性。
下图展示了一个简单的图,图中的边既可以是有向的,也可以是无向的,并且边的粗细程度也代表了权重的大小:
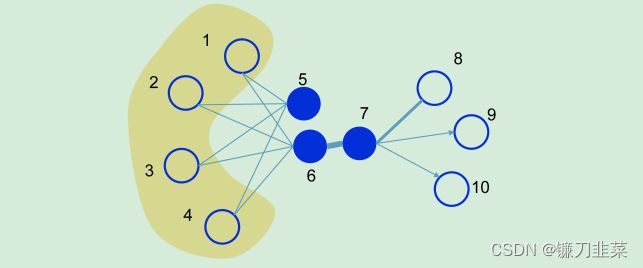
一阶相似度
一阶阶相似度用于描述图中成对顶点之间的局部相似度,形式化描述为若 u , v u,v u,v之间存在直连边,则边权 w u v w_{uv} wuv 即为两个顶点的相似度,若不存在直连边,则 1 阶相似度为0。 如上图,6和7之间存在直连边,且边权较大,则认为两者相似且1阶相似度较高,而5和6之间不存在直连边,则两者间1阶相似度为0。
二阶相似度
仅有1阶相似度就够了吗?显然不够,如上图,虽然5和6之间不存在直连边,但是他们有很多相同的邻居顶点(1,2,3,4),这其实也可以表明5和6是相似的,而2阶相似度就是用来描述这种关系的。 形式化定义为,令 p u = ( w u , 1 , . . . , w u , ∣ V ∣ ) p_u=(w_{u,1},...,w_{u,|V|}) pu=(wu,1,...,wu,∣V∣)表示顶点 u u u与所有其他顶点间的1阶相似度,则 u u u与 v v v的2阶相似度可以通过 p u p_u pu 和 p v p_v pv 的相似度表示。若 u u u与 v v v之间不存在相同的邻居顶点,则2阶相似度为0。
优化目标
(1)一阶
对于每一条无向边 ( i , j ) (i,j) (i,j),定义顶点 v i v_i vi和 v j v_j vj之间的联合概率为 p 1 ( v i , v j ) = 1 1 + e x p ( − u ⃗ i ⋅ u ⃗ j ) p_1(v_i,v_j)=\frac{1}{1+exp(-\vec{u}_i \cdot \vec{u}_j)} p1(vi,vj)=1+exp(−ui⋅uj)1其中 u ⃗ i \vec{u}_i ui为顶点 v i v_i vi的低维向量表示。该公式可以看作一个内积模型,计算两个item之间的匹配程度。
同时定义经验分布 p ^ 1 = w i j W \hat{p}_1=\frac{w_{ij}}{W} p^1=Wwij, W = ∑ ( i , j ) ∈ E w i j W=\sum_{(i,j)\in E}w_{ij} W=∑(i,j)∈Ewij
优化目标为最小化: O 1 = d ( p ^ 1 , ( ⋅ , ⋅ ) , p ^ 1 ( ⋅ , ⋅ ) ) O_1=d(\hat{p}_1,(\cdot, \cdot),\hat{p}_1(\cdot, \cdot)) O1=d(p^1,(⋅,⋅),p^1(⋅,⋅))其中d(\cdot, \cdot)是两个分布的距离,常用的衡量两个概率分布差异的指标为KL散度,使用KL散度并忽略常数项后有 O 1 = − ∑ ( i , j ) ∈ E w i j log p i ( v i , v j ) O_1=-\sum_{(i,j)\in E}w_{ij} \log p_i(v_i,v_j) O1=−(i,j)∈E∑wijlogpi(vi,vj)
一阶相似度只能用于无向图当中。
(2)二阶
对于每个顶点维护两个embedding向量,一个是该顶点本身的表示向量,一个是该点作为其他顶点的上下文顶点时的表示向量。
对于有向边 ( i , j ) (i,j) (i,j),定义给定顶点 v i v_i vi条件下,产生上下文(邻居)顶点 v j v_j vj的概率为 p 2 ( v j ∣ v i ) = e x p ( u ⃗ j ⋅ u ⃗ i ) ∑ k = 1 ∣ V ∣ e x p ( u ⃗ k T ⋅ u ⃗ i ) p_2(v_j|v_i)=\frac{exp(\vec{u}_j\cdot \vec{u}_i)}{\sum_{k=1}^{|V|}exp(\vec{u}_k^T\cdot \vec{u}_i)} p2(vj∣vi)=∑k=1∣V∣exp(ukT⋅ui)exp(uj⋅ui)其中 ∣ V ∣ |V| ∣V∣为上下文顶点的个数。
优化目标为 O 2 = ∑ i ∈ V λ i d ( p ^ 2 ( ⋅ ∣ v i ) , p 2 ( ⋅ ∣ v i ) ) O_2=\sum_{i\in V}\lambda_i d(\hat{p}_2(\cdot|v_i),p_2(\cdot|v_i)) O2=i∈V∑λid(p^2(⋅∣vi),p2(⋅∣vi))其中 λ i \lambda_i λi为控制节点重要性的因子,可以通过顶点的度数或者PageRank等方法估计得到。
经验分布定义为: p ^ 2 ( v j ∣ v i ) = w i j d i \hat{p}_2(v_j|v_i)=\frac{w_{ij}}{d_i} p^2(vj∣vi)=diwij, w i j w_{ij} wij是边 ( i , j ) (i,j) (i,j)是边权, d i d_i di是顶点 v i v_i vi的出度,对于带权图, d i = ∑ k ∈ N ( I ) W i k d_i=\sum_{k\in N(I)}W_{ik} di=∑k∈N(I)Wik
使用KL散度并设 λ i = d i \lambda_i=d_i λi=di,忽略常数项,有 O 2 = − ∑ ( i , j ) ∈ E w i j log p 2 ( v j ∣ v i ) O_2=-\sum_{(i,j)\in E} w_{ij}\log p_2(v_j|v_i) O2=−(i,j)∈E∑wijlogp2(vj∣vi)
优化技巧
(1)Negative Sampling(负采样)
由于计算2阶相似度时,softmax函数的分母计算需要遍历所有顶点,这是非常低效的,论文采用了负采样优化的技巧,目标函数变为:
log σ ( u ⃗ j T ⋅ u ⃗ i ) + ∑ i = 1 K E v n ∼ P n ( v ) [ − log σ ( u ⃗ n T ⋅ u ⃗ i ) ] \log \sigma(\vec{u}_j^T\cdot \vec{u}_i)+\sum_{i=1}^K E_{v_n\sim P_n(v)}[-\log \sigma(\vec{u}_n^T\cdot \vec{u}_i)] logσ(ujT⋅ui)+i=1∑KEvn∼Pn(v)[−logσ(unT⋅ui)]其中 K K K是负边的个数。论文中使用 P n ( v ) ∝ d v 3 / 4 P_n(v)\propto d_v^{3/4} Pn(v)∝dv3/4, d v d_v dv是顶点 v v v的出度。
(2)Edge Sampling(边采样)
注意到我们的目标函数在log之前还有一个权重系数 w i j w_{ij} wij,在使用梯度下降方法优化参数时, w i j w_{ij} wij会直接乘在梯度上。如果图中的边权方差很大,则很难选择一个合适的学习率。若使用较大的学习率那么对于较大的边权可能会引起梯度爆炸,较小的学习率对于较小的边权则会导致梯度过小。
对于上述问题,如果所有边权相同,那么选择一个合适的学习率会变得容易。这里采用了将带权边拆分为等权边的一种方法,假如一个权重为 w w w的边,则拆分后为 w w w个权重为1的边。这样可以解决学习率选择的问题,但是由于边数的增长,存储的需求也会增加。
另一种方法则是从原始的带权边中进行采样,每条边被采样的概率正比于原始图中边的权重,这样既解决了学习率的问题,又没有带来过多的存储开销。
这里的采样算法使用的是Alias算法,Alias是一种 O ( 1 ) O(1) O(1)时间复杂度的离散事件抽样算法。具体内容可以参考Alias Method:时间复杂度O(1)的离散采样方法
示例代码
首先输入就是两个顶点的编号,然后分别拿到各自对应的embedding向量,最后输出内积的结果。 真实 label 定义为1或者-1。最终模型输出内积,然后可以对内积结果进行优化。

这里的实现中把1阶和2阶的方法融合到一起了,可以通过超参数order控制是分开优化还是联合优化,论文推荐分开优化。
import math
import random
import numpy as np
import tensorflow as tf
from tensorflow.python.keras import backend as K
from tensorflow.python.keras.layers import Embedding, Input, Lambda
from tensorflow.python.keras.models import Model
def line_loss(y_true, y_pred):
return -K.mean(K.log(K.sigmoid(y_true * y_pred)))
def create_model(numNodes, embedding_size, order='second'):
v_i = Input(shape=(1,))
v_j = Input(shape=(1,))
first_emb = Embedding(numNodes, embedding_size, name='first_emb')
second_emb = Embedding(numNodes, embedding_size, name='second_emb')
context_emb = Embedding(numNodes, embedding_size, name='context_emb')
v_i_emb = first_emb(v_i)
v_j_emb = first_emb(v_j)
v_i_emb_second = second_emb(v_i)
v_j_context_emb = context_emb(v_j)
first = Lambda(lambda x: tf.reduce_sum(
x[0] * x[1], axis=-1, keepdims=False), name='first_order')([v_i_emb, v_j_emb])
second = Lambda(lambda x: tf.reduce_sum(
x[0] * x[1], axis=-1, keepdims=False), name='second_order')([v_i_emb_second, v_j_context_emb])
if order == 'first':
output_list = [first]
elif order == 'second':
output_list = [second]
else:
output_list = [first, second]
model = Model(inputs=[v_i, v_j], outputs=output_list)
return model, {'first': first_emb, 'second': second_emb}
def preprocess_nxgraph(graph):
node2idx = {}
idx2node = []
node_size = 0
for node in graph.nodes():
node2idx[node] = node_size
idx2node.append(node)
node_size += 1
return idx2node, node2idx
def create_alias_table(area_ratio):
"""
:param area_ratio: sum(area_ratio)=1
:return: accept,alias
"""
l = len(area_ratio)
accept, alias = [0] * l, [0] * l
small, large = [], []
area_ratio_ = np.array(area_ratio) * l
for i, prob in enumerate(area_ratio_):
if prob < 1.0:
small.append(i)
else:
large.append(i)
while small and large:
small_idx, large_idx = small.pop(), large.pop()
accept[small_idx] = area_ratio_[small_idx]
alias[small_idx] = large_idx
area_ratio_[large_idx] = area_ratio_[large_idx] - (1 - area_ratio_[small_idx])
if area_ratio_[large_idx] < 1.0:
small.append(large_idx)
else:
large.append(large_idx)
while large:
large_idx = large.pop()
accept[large_idx] = 1
while small:
small_idx = small.pop()
accept[small_idx] = 1
return accept, alias
def alias_sample(accept, alias):
"""
:param accept:
:param alias:
:return: sample index
"""
N = len(accept)
i = int(np.random.random() * N)
r = np.random.random()
if r < accept[i]:
return i
else:
return alias[i]
class LINE:
def __init__(self, graph, embedding_size=8, negative_ratio=5, order='second'):
"""
:param graph:
:param embedding_size:
:param negative_ratio:
:param order: 'first','second','all'
"""
if order not in ['first', 'second', 'all']:
raise ValueError('mode must be fisrt,second,or all')
self.graph = graph
self.idx2node, self.node2idx = preprocess_nxgraph(graph)
self.use_alias = True
self.rep_size = embedding_size
self.order = order
self._embeddings = {}
self.negative_ratio = negative_ratio
self.order = order
self.node_size = graph.number_of_nodes()
self.edge_size = graph.number_of_edges()
self.samples_per_epoch = self.edge_size * (1 + negative_ratio)
self._gen_sampling_table()
self.reset_model()
def reset_training_config(self, batch_size, times):
self.batch_size = batch_size
self.steps_per_epoch = ((self.samples_per_epoch - 1) // self.batch_size + 1) * times
def reset_model(self, opt='adam'):
self.model, self.embedding_dict = create_model(self.node_size, self.rep_size, self.order)
self.model.compile(opt, line_loss)
self.batch_it = self.batch_iter(self.node2idx)
def _gen_sampling_table(self):
# create sampling table for vertex
power = 0.75
numNodes = self.node_size
node_degree = np.zeros(numNodes) # out degree
node2idx = self.node2idx
for edge in self.graph.edges():
node_degree[node2idx[edge[0]]] += self.graph[edge[0]][edge[1]].get('weight', 1.0)
total_sum = sum([math.pow(node_degree[i], power) for i in range(numNodes)])
norm_prob = [float(math.pow(node_degree[j], power))/total_sum for j in range(numNodes)]
self.node_accept, self.node_alias = create_alias_table(norm_prob)
# create sampling table for edge
numEdges = self.graph.number_of_edges()
total_sum = sum([self.graph[edge[0]][edge[1]].get('weight', 1.0) for edge in self.graph.edges()])
norm_prob = [self.graph[edge[0]][edge[1]].get('weight', 1.0) * numEdges / total_sum for edge in self.graph.edges()]
self.edge_accept, self.edge_alias = create_alias_table(norm_prob)
def batch_iter(self, node2idx):
edges = [(node2idx[x[0]], node2idx[x[1]]) for x in self.graph.edges()]
data_size = self.graph.number_of_edges()
shuffle_indices = np.random.permutation(np.arange(data_size))
# positive or negative mod
mod = 0
mod_size = 1 + self.negative_ratio
h = []
t = []
sign = 0
count = 0
start_index = 0
end_index = min(start_index + self.batch_size, data_size)
while True:
if mod == 0:
h = []
t = []
for i in range(start_index, end_index):
if random.random() >= self.edge_accept[shuffle_indices[i]]:
shuffle_indices[i] = self.edge_alias[shuffle_indices[i]]
cur_h = edges[shuffle_indices[i]][0]
cur_t = edges[shuffle_indices[i]][1]
h.append(cur_h)
t.append(cur_t)
sign = np.ones(len(h))
else:
sign = np.ones(len(h)) * -1
t = []
for i in range(len(h)):
t.append(alias_sample(self.node_accept, self.node_alias))
if self.order == 'all':
yield ([np.array(h), np.array(t)], [sign, sign])
else:
yield ([np.array(h), np.array(t)], [sign])
mod += 1
mod %= mod_size
if mod == 0:
start_index = end_index
end_index = min(start_index + self.batch_size, data_size)
if start_index >= data_size:
count += 1
mod = 0
h = []
shuffle_indices = np.random.permutation(np.arange(data_size))
start_index = 0
end_index = min(start_index + self.batch_size, data_size)
def get_embeddings(self, ):
self._embeddings = {}
if self.order == 'first':
embeddings = self.embedding_dict['first'].get_weights()[0]
elif self.order == 'second':
embeddings = self.embedding_dict['second'].get_weights()[0]
else:
embeddings = np.hstack((self.embedding_dict['first'].get_weights()[0], self.embedding_dict['second'].get_weights()[0]))
idx2node = self.idx2node
for i, embedding in enumerate(embeddings):
self._embeddings[idx2node[i]] = embedding
return self._embeddings
def train(self, batch_size=1024, epochs=1, initial_epoch=0, verbose=1, times=1):
self.reset_training_config(batch_size, times)
hist = self.model.fit_generator(self.batch_it, epochs=epochs, initial_epoch=initial_epoch, steps_per_epoch=self.steps_per_epoch, verbose=verbose)
return hist
执行训练并输出节点embedding:
import networkx as nx
# 构建图
G = nx.Graph()
G.add_edges_from([(1, 2), (1, 3), (2, 4), (2, 5), (3, 6), (3, 7), (4, 8), (4, 9)])
model = LINE(G,embedding_size=16,order='second')
model.train(batch_size=1,epochs=10,verbose=2)
embeddings = model.get_embeddings()
# 打印节点的嵌入向量
for node in G.nodes():
print(f"Node {node}: {embeddings[node]}")
3. SDNE
SDNE没有采用随机游走的方法而是使用自动编码器来同时优化一阶和二阶相似度,学习得到的向量表示保留局部和全局结构,并且对稀疏网络具有鲁棒性。
正如前面LINE算法所讲,一阶相似度表征了边连接的成对节点之间的局部相似性。如果网络中的两个节点相连,则认为它们是相似的。二阶相似度表示节点邻域结构的相似性,它能够了表征全局的网络结构。如果两个节点共享许多邻居,则它们趋于相似。

图2 半监督深度模型SDNE框架。它主要由两部分组成编码器及解码器。编码器是图片中红色的圈圈,解码器是蓝色的圈圈,绿色代表的是节点的表示向量。模型的输入 x i x_i xi是图的邻接矩阵的第 i i i行,表示的是节点 i i i和网络中所有节点的连接情况,通过编码器将输入映射到低维向量空间,得到低维向量表示 y i ( K ) y_i^{(K)} yi(K),再通过解码器重构回去。因此具有大量相同邻居的节点通过自编码器网络学到的embedding表示会比较相似,这保持了图网络的二阶相似性。另外,对于有直连边的节点对,SDNE会约束两个节点的embedding表示接近,从而保持了图网络的一阶相似性。
SDNE的具体做法是使用自动编码器来保持一阶和二阶网络邻近度。它通过联合优化这两个近似值来实现这一点。该方法利用高度非线性函数来获得嵌入。模型由两部分组成:无监督和监督。前者包括一个自动编码器,目的是寻找一个可以重构其邻域的节点的嵌入。后者基于拉普拉斯特征映射,当相似顶点在嵌入空间中彼此映射得很远时,该特征映射会受到惩罚。
SDNE的损失函数如下所示,由三部分组成:一阶相似度损失、二阶相似度损失和L2正则项。 L m i n = L 2 n d + α L 1 s t + v L r e g \mathcal{L}_{min}=\mathcal{L}_{2nd}+\alpha\mathcal{L}_{1st}+v\mathcal{L}_{reg} Lmin=L2nd+αL1st+vLreg
L r e g = 1 2 ∑ k = 1 K ( ∣ ∣ W ( k ) ∣ ∣ F 2 + ∣ ∣ W ^ ( k ) ∣ ∣ F 2 ) \mathcal{L}_{reg}=\frac{1}{2}\sum_{k=1}^K(||W^{(k)}||_F^2+||\hat{W}^{(k)}||_F^2) Lreg=21k=1∑K(∣∣W(k)∣∣F2+∣∣W^(k)∣∣F2)
第一部分是邻居节点之间的一阶相似性损失: L 1 s t = ∑ i , j = 1 n s i , j ∣ ∣ y i ( K ) − y j ( K ) ∣ ∣ 2 2 = ∑ i , j = 1 n s i , j ∣ ∣ y i − y j ∣ ∣ 2 2 \mathcal{L}_{1st}=\sum_{i,j=1}^ns_{i,j}||y_i^{(K)}-y_j^{(K)}||_2^2=\sum_{i,j=1}^ns_{i,j}||y_i-y_j||_2^2 L1st=i,j=1∑nsi,j∣∣yi(K)−yj(K)∣∣22=i,j=1∑nsi,j∣∣yi−yj∣∣22
这里 s i , j s_{i,j} si,j 代表两个节点之前的连接关系(在无权网络中1代表由连接,0代表无连接), y i y_i yi 代表的是节点 i i i 的嵌入向量,也就是前面模型中的绿色节点。一阶相似性的目的很简单,就是为了让邻居节点之间的表示向量更接近,所以在损失函数中希望他们之间表示向量差异小一些。
二阶相似性,简单的理解就是希望具有更多相似邻居的节点之间的表示向量更相似,它的损失由自编码器的重构情况构成的: L 2 n d = ∑ i = 1 n ∣ ∣ ( x ^ i − x i ) ⊙ b i ∣ ∣ 2 2 = ∣ ∣ ( X ^ − X ) ⊙ B ∣ ∣ F 2 \mathcal{L}_{2nd}=\sum_{i=1}^n||(\hat{x}_i-x_i)\odot b_i||_2^2=||(\hat{X}-X)\odot B||_F^2 L2nd=i=1∑n∣∣(x^i−xi)⊙bi∣∣22=∣∣(X^−X)⊙B∣∣F2
其中 x i x_i xi是节点 i i i的邻接向量,也就是取出节点在邻接矩阵中它的那行值。这里乘以B的目的是为了区分0,1值的区别,因为一个节点的邻居向量可能是这样的:0000100000000010001,其中0占了大部分,1只有少部分,为了增强1的作用所以让它乘以一个值(文章中取的是5)。无论是Deepwalk,LINE,Node2vec它们的一阶及二阶相似性原理都是差不多的,一阶相似性都是希望有连接节点之间相似度高一些,然后二阶就是具有更多相同邻居节点的节点之间的表示向量相似一些。

示例代码
import torch
import numpy as np
import networkx as nx
import scipy.sparse as sparse
class SDNEModel(torch.nn.Module):
def __init__(self, input_dim, hidden_layers, alpha, beta, device='cpu'):
'''Structural Deep Network Embedding(SDNE)
:param input_dim: 节点数量 node_size
:param hidden_layers: AutoEncoder中间层数
:param alpha: 对于1st_loss的系数
:param beta: 对于2nd_loss中对非0项的惩罚
:param device:
'''
super(SDNEModel, self).__init__()
self.alpha = alpha
self.beta = beta
self.device = device
input_dim_copy = input_dim
layers = []
for layer_dim in hidden_layers:
layers.append(torch.nn.Linear(input_dim, layer_dim))
layers.append(torch.nn.ReLU())
input_dim = layer_dim
self.encoder = torch.nn.Sequential(*layers)
layers = []
for layer_dim in reversed(hidden_layers[:-1]):
layers.append(torch.nn.Linear(input_dim, layer_dim))
layers.append(torch.nn.ReLU())
input_dim = layer_dim
# 最后加一层输入的维度
layers.append(torch.nn.Linear(input_dim, input_dim_copy))
layers.append(torch.nn.ReLU())
self.decoder = torch.nn.Sequential(*layers)
def forward(self, A, L):
'''输入节点的邻接矩阵和拉普拉斯矩阵,主要计算方式参考论文
:param A: adjacency_matrix, dim=(m, n)
:param L: laplace_matrix, dim=(m, m)
:return:
'''
Y = self.encoder(A)
A_hat = self.decoder(Y)
# loss_2nd 二阶相似度损失函数
beta_matrix = torch.ones_like(A)
mask = A != 0
beta_matrix[mask] = self.beta
loss_2nd = torch.mean(torch.sum(torch.pow((A - A_hat) * beta_matrix, 2), dim=1))
# loss_1st 一阶相似度损失函数 论文公式(9) alpha * 2 *tr(Y^T L Y)
loss_1st = self.alpha * 2 * torch.trace(torch.matmul(torch.matmul(Y.transpose(0,1), L), Y))
return loss_2nd + loss_1st
def process_nxgraph(graph):
node2idx = {}
idx2node = []
node_size = 0
for node in graph.nodes():
node2idx[node] = node_size
idx2node.append(node)
node_size += 1
return idx2node, node2idx
class Regularization(torch.nn.Module):
def __init__(self, model, gamma=0.01, p=2, device="cpu"):
'''
:param model:构建好的模型
:param gamma:系数
:param p:当p=0表示L2正则化,p=1表示L1正则化
'''
super().__init__()
if gamma <= 0:
print("param weight_decay can not be <= 0")
exit(0)
self.model = model
self.gamma = gamma
self.p = p
self.device = device
self.weight_list = self.get_weight_list(model) # 取出参数的列表
self.weight_info = self.get_weight_info(self.weight_list) # 打印参数的信息
def to(self, device):
super().to(device)
self.device = device
return self
def forward(self, model):
self.weight_list = self.get_weight_list(model)
reg_loss = self.regulation_loss(self.weight_list, self.gamma, self.p)
return reg_loss
def regulation_loss(self, weight_list, gamma, p=2):
reg_loss = 0
for name, w in weight_list:
l2_reg = torch.norm(w, p=p)
reg_loss += l2_reg
reg_loss = reg_loss * gamma
return reg_loss
def get_weight_list(self, model):
weight_list = []
# 返回参数的名字和参数自己
for name, param in model.named_parameters():
# 这里只取weight 未取bias
if 'weight' in name:
weight = (name, param)
weight_list.append(weight)
return weight_list
def get_weight_info(self, weight_list):
# 打印被正则化的参数的名称
print("#"*10, "regulations weight", "#"*10)
for name, param in weight_list:
print(name)
print("#"*25)
class SDNE(torch.nn.Module):
def __init__(self, graph, hidden_layers=None, alpha=1e-5, beta=5, gamma=1e-5, device="cpu"):
super().__init__()
self.graph = graph
self.idx2node, self.node2idx = process_nxgraph(graph)
self.node_size = graph.number_of_nodes()
self.edge_size = graph.number_of_edges()
self.sdne = SDNEModel(self.node_size, hidden_layers, alpha, beta)
self.device = device
self.embeddings = {}
self.gamma = gamma
adjacency_matrix, laplace_matrix = self.__create_adjacency_laplace_matrix()
self.adjacency_matrix = torch.from_numpy(adjacency_matrix.toarray()).float().to(self.device)
self.laplace_matrix = torch.from_numpy(laplace_matrix.toarray()).float().to(self.device)
def fit(self, batch_size=512, epochs=1, initial_epoch=0, verbose=1):
num_samples = self.node_size
self.sdne.to(self.device)
optimizer = torch.optim.Adam(self.sdne.parameters())
if self.gamma:
regularization = Regularization(self.sdne, gamma=self.gamma)
if batch_size >= self.node_size:
batch_size = self.node_size
print('batch_size({0}) > node_size({1}),set batch_size = {1}'.format(batch_size, self.node_size))
for epoch in range(initial_epoch, epochs):
loss_epoch = 0
optimizer.zero_grad()
loss = self.sdne(self.adjacency_matrix, self.laplace_matrix)
if self.gamma:
reg_loss = regularization(self.sdne)
# print("reg_loss:", reg_loss.item(), reg_loss.requires_grad)
loss = loss + reg_loss
loss_epoch += loss.item()
loss.backward()
optimizer.step()
if verbose > 0:
print('Epoch {0}, loss {1} . >>> Epoch {2}/{3}'.format(epoch + 1, round(loss_epoch / num_samples, 4), epoch+1, epochs))
else:
steps_per_epoch = (self.node_size - 1) // batch_size + 1
for epoch in range(initial_epoch, epochs):
loss_epoch = 0
for i in range(steps_per_epoch):
idx = np.arange(i * batch_size, min((i+1) * batch_size, self.node_size))
A_train = self.adjacency_matrix[idx, :]
L_train = self.laplace_matrix[idx][:,idx]
# print(A_train.shape, L_train.shape)
optimizer.zero_grad()
loss = self.sdne(A_train, L_train)
loss_epoch += loss.item()
loss.backward()
optimizer.step()
if verbose > 0:
print('Epoch {0}, loss {1} . >>> Epoch {2}/{3}'.format(epoch + 1, round(loss_epoch / num_samples, 4), epoch + 1, epochs))
def get_embeddings(self):
if not self.embeddings:
self.__get_embeddings()
embeddings = self.embeddings
return embeddings
def __get_embeddings(self):
embeddings = {}
with torch.no_grad():
self.sdne.eval()
embed = self.sdne.encoder(self.adjacency_matrix)
for i, embedding in enumerate(embed.numpy()):
embeddings[self.idx2node[i]] = embedding
self.embeddings = embeddings
def __create_adjacency_laplace_matrix(self):
node_size = self.node_size
node2idx = self.node2idx
adjacency_matrix_data = []
adjacency_matrix_row_index = []
adjacency_matrix_col_index = []
for edge in self.graph.edges():
v1, v2 = edge
edge_weight = self.graph[v1][v2].get("weight", 1.0)
adjacency_matrix_data.append(edge_weight)
adjacency_matrix_row_index.append(node2idx[v1])
adjacency_matrix_col_index.append(node2idx[v2])
adjacency_matrix = sparse.csr_matrix((adjacency_matrix_data,(adjacency_matrix_row_index, adjacency_matrix_col_index)),shape=(node_size, node_size))
# L = D - A 有向图的度等于出度和入度之和; 无向图的领接矩阵是对称的,没有出入度之分直接为每行之和
# 计算度数
adjacency_matrix_ = sparse.csr_matrix((adjacency_matrix_data+adjacency_matrix_data,(adjacency_matrix_row_index+adjacency_matrix_col_index,adjacency_matrix_col_index+adjacency_matrix_row_index)), shape=(node_size, node_size))
degree_matrix = sparse.diags(adjacency_matrix_.sum(axis=1).flatten().tolist()[0])
laplace_matrix = degree_matrix - adjacency_matrix_
return adjacency_matrix, laplace_matrix
# 构建图
G = nx.Graph()
G.add_edges_from([(1, 2), (1, 3), (2, 4), (2, 5), (3, 6), (3, 7), (4, 8), (4, 9)])
model = SDNE(G, hidden_layers=[64, 16])
model.fit(batch_size=2, epochs=10)
embeddings = model.get_embeddings()
# 打印节点的嵌入向量
for node in G.nodes():
print(f"Node {node}: {embeddings[node]}")
4. Node2vec
Node2Vec算法在DeepWalk算法上做了一点小改进,主要是改变了随机游走生成序列的过程,使得在学习embedding的过程中会对图节点的同质性(homophily)和结构性(structural equivalence)做权衡,得到序列之后同样使用skipGram算法来学习节点的embedding表示。
同质性和结构性的含义可以从下图进行说明,同质性表示两个相连的节点应该具有相似的embedding表示,如图中节点 u 和节点 S 1 S_1 S1直接相连,则他们的embedding应该距离较近。结构性表示两个结构上相似的两个节点应该具有相似的embedding表示,如图中节点 u 和节点 S 6 S_6 S6分别处在两个集群的中心位置,则这两个节点的embedding应该比较相似。
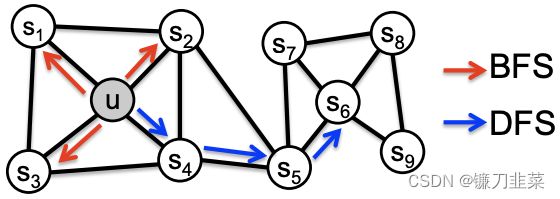
通常使用DFS表达网络的同质性,使用BFS表达网络的结构性。

从节点 v v v跳转到下一个节点 x x x的概率为:
π v x = α p q ( t , x ) ⋅ w v x \pi_{vx}=\alpha_{pq}(t,x)\cdot w_{vx} πvx=αpq(t,x)⋅wvx
其中 w v x w_{vx} wvx是边VX的权重, α p q ( t , x ) \alpha_{pq}(t,x) αpq(t,x)的定义如下:
α p q ( t , x ) = { 1 p if d t x = 0 1 if d t x = 1 1 q if d t x = 2 \alpha _{pq}(t,x)=\begin{cases}\frac{1}{p} & \text{ if } d_{tx}=0 \\1 & \text{ if } d_{tx}=1 \\\frac{1}{q} & \text{ if } d_{tx}=2\end{cases} αpq(t,x)=⎩ ⎨ ⎧p11q1 if dtx=0 if dtx=1 if dtx=2
其中 d t x d_{tx} dtx表示节点 t t t到节点 x x x的距离:
- 如果两个节点为相同的节点, d t x = 0 d_{tx}=0 dtx=0
- 如果两个节点直接相连, d t x = 1 d_{tx}=1 dtx=1
- 如果两个节点不相连, d t x = 2 d_{tx}=2 dtx=2
参数 p 和 q 共同控制着随机游走的倾向性:
- 参数 p 被称为返回参数(return parameter),p越小,节点返回 t 的概率越高,图的遍历越倾向于BFS,越趋向于表示图的结构性。
- 参数 q 被称为进出参数(in-out parameter),q越小,遍历到远处节点的概率越高,图的遍历越倾向于DFS,越趋向于表示图的同质性。
- 可以通过设置p,q的值,来权衡graph embedding表达的结果的倾向性。当p=1,q=1时,游走方式就等同于DeepWalk中的随机游走。
使用以上规则生成序列,然后将序列输入模型计算每个节点的Emedding。由于Node2Vec所体现的网络的同质性和结构性在推荐系统中也是可以被很直观地解释的。同质性相同的物品很可能是同品类、同属性、或者经常被一同购买的物品,而结构性相同的物品则是各品类的爆款、各品类的最佳凑单商品等拥有类似趋势或者结构性属性的物品。
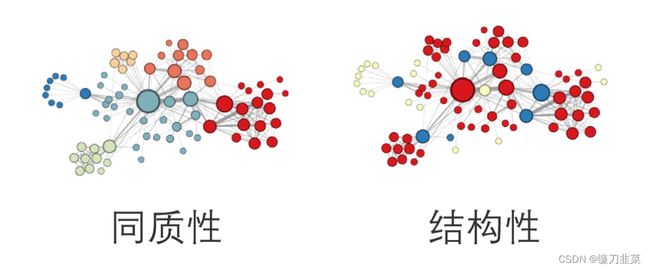
二者在推荐系统中都是非常重要的特征表达。由于Node2Vec的这种灵活性,以及发掘不同特征的能力,我们可以把不同倾向表达结果的embedding拼接起来,得到更丰富的embedding特征;也可以把不同Node2Vec生成的Embedding融合共同输入后续深度学习网络,以保留物品的不同特征信息。
总之,node2vec是一种综合考虑DFS邻域和BFS邻域的graph embedding方法。简单来说,可以看作是deepwalk的一种扩展,是结合了DFS和BFS随机游走的deepwalk。
node2vec核心代码:

node2vec有一个三方库,可以通过pip进行安装:
pip install node2vec
简单用法:
import networkx as nx
from node2vec import Node2Vec
# 构建图
G = nx.Graph()
G.add_edges_from([(1, 2), (1, 3), (2, 4), (2, 5), (3, 6), (3, 7), (4, 8), (4, 9)])
# Precompute probabilities and generate walks - **ON WINDOWS ONLY WORKS WITH workers=1**
node2vec = Node2Vec(G, dimensions=16, walk_length=10, num_walks=100, workers=4) # Use temp_folder for big graphs
# Embed nodes
model = node2vec.fit(window=10, min_count=0, batch_words=4)
from node2vec.edges import AverageEmbedder
from node2vec.edges import HadamardEmbedder
from node2vec.edges import WeightedL1Embedder
from node2vec.edges import WeightedL2Embedder
edges_embs = HadamardEmbedder(keyed_vectors=model.wv)
# Look for embeddings on the fly - here we pass normal tuples
print(edges_embs[('1', '2')])
得到节点1到节点2之间的embedding:

得到每个节点的embeddings:
embeddings = model.wv.vectors
for ix, node in enumerate(G.nodes()):
print(f"Node {node}: {embeddings[ix]}")
5. Struc2vec
2017发布的Struc2Vec可以看作是从另一个角度去抽取图上的某些特征,DeepWalk学习的是近邻相似性,LINE学习的是一阶近邻和二阶近邻相似性,Node2Vec学习近邻相似性和结构相似性,但是Node2Vec其实无法学习到充分的结构相似性,因为random walk的步数毕竟是有限的,如果两个节点之间的距离非常远,则很难去学习到所谓的结构相似性,而struc2vec则是直接针对于结构相似性进行学习。

它的核心思想是:
-
忽略节点和边的属性以及它们在网络中的位置来评估节点间的结构相似性,仅考虑节点的局部结构。两个节点的结构相似度的直观评判标准是:如果两个节点的度相同,它们在结构上是相似的;如果两个节点的邻居的度也相同,它们的结构相似度就更高了。

定义 R k ( u ) R_k(u) Rk(u)表示在khop的顶点集合, S ( s ) S(s) S(s)表示集合S度的有序序列, g ( D 1 , D 2 ) g(D_1,D_2) g(D1,D2)表示D1与D2之间的距离。 f ( u , v ) f(u,v) f(u,v)表示在khop邻居的u和v的相似性。 -
建立一个分层结构来衡量节点的结构相似性:在最底层,结构相似性仅取决于节点度;在最高层,结构相似性取决于整个网络的信息。
具体过程如下:
首先,构建带权多层图,对于图 G = ( V , E ) G=(V,E) G=(V,E),按以下描述构建一个带权多层图M:
M的第k层是由节点集合V组成的带权无向完全图,其中每对节点u、v间的边权重定义为 w k ( u , v ) = e − f k ( u , v ) w_k(u,v)=e^{-f_k(u,v)} wk(u,v)=e−fk(u,v)(与它们之间的结构距离成反比)。
层与层之间权重的对应关系为:

P指在下一次采样时,有 p 的概率在本层游走,有 1-p 的概率进行上下游切换。所以 p 的计算公式分为两种情况:
(1)在本层游走时
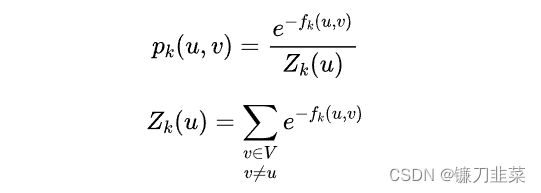
(2)在上下游切换时

总体上看:

- 然后节点通过上述规则游走得到游走序列,用Skip-gram生成embedding。
简单来说,Struct2Vec的步骤分为三步:1. 获取每一层的顶点对距离 2. 根据顶点对距离构建带权层次图 3. 在带权层次图中随机游走采样顶点序列。
Struc2vec对图的结构信息进行捕获,在其结构重要性大于邻居重要性时,有较好的效果。
图嵌入方法
关于整个图嵌入的方式这里介绍具有代表性的graph2vec。
1. Graph2vec
图嵌入是将整个图用一个向量表示的方法,Graph2vec同样是基于skip-gram思想,把整个图编码进向量空间, 类似文档嵌入doc2vec, doc2vec在输入中获取文档的ID,并通过最大化文档预测随机单词的可能性进行训练。
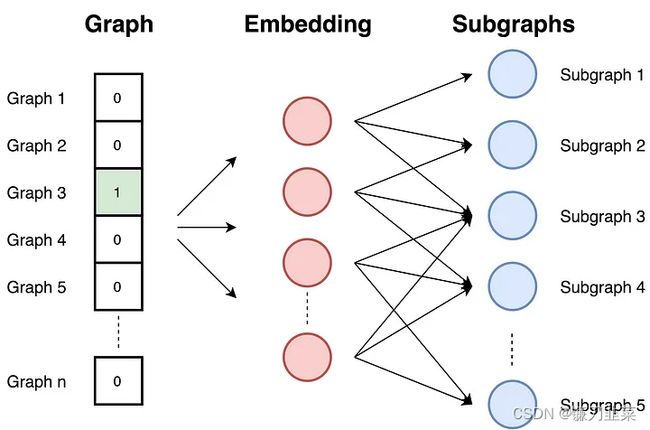
Graph2vec同样由三个步骤构成:
- 采样并重新标记图中的所有子图。子图是出现在所选节点周围的一组节点。
- 训练skip-gram模型。类似于文档doc2vec, 由于文档是单词集,而图是子图集,在此阶段,对skip-gram模型进行训练。经过训练,可以最大程度地预测输入中存在于图中的子图的概率。
- 计算。通过在输入处提供子图的id索引向量来计算嵌入。
其他的方法
以上提到的是几个常用的方法,但是除此之外还有非常多的方法和模型值得学习
- Node embedding: LLE, Laplacian Eigenmaps, Graph Factorization, GraRep, HOPE, DNGR, GCN, LINE
- Graph embedding approaches: Patchy-san, sub2vec (embed subgraphs), WL kernel andDeep WL kernels
总结
本文结合ChatGPT和相关代码介绍了Graph embedding是什么,为什么要采用Graph embedding,以及进行embedding时需要满足的性质。进一步简单介绍了node-level的几个经典的方法:DeepWalk, LINE, SDNE等以及graph-levle的graph2vec。
注意:这里介绍的都是基于同质图的嵌入方法!!!
相关资料
- Graph Embeddings — The Summary
- DeepWalk:算法原理,实现和应用
- DeepWalk原理与代码实战
- LINE:算法原理,实现和应用
- Graph Embedding 方法之 LINE 原理解读
- Alias Method:时间复杂度O(1)的离散采样方法
- SDNE(Structural Deep Network Embedding)理论及pytorch实现
- Graph Embedding(二)
- Graph Embedding(三)
- Graph Embedding 图表示学习的原理及应用
- Node2Vec showcase
- Node classification with weighted Node2Vec
- Node2Vec
- Struc2Vec:算法原理,实现和应用
- Struc2vec: learning node representations from structural identity



