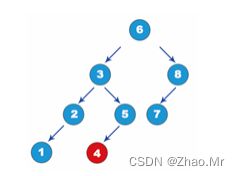
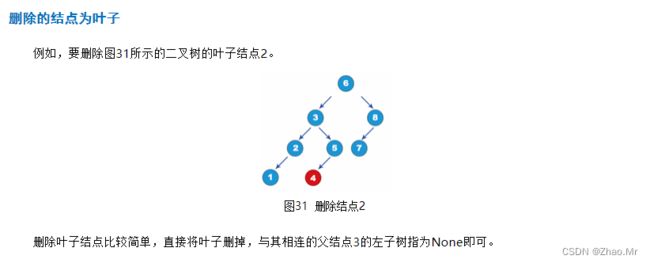
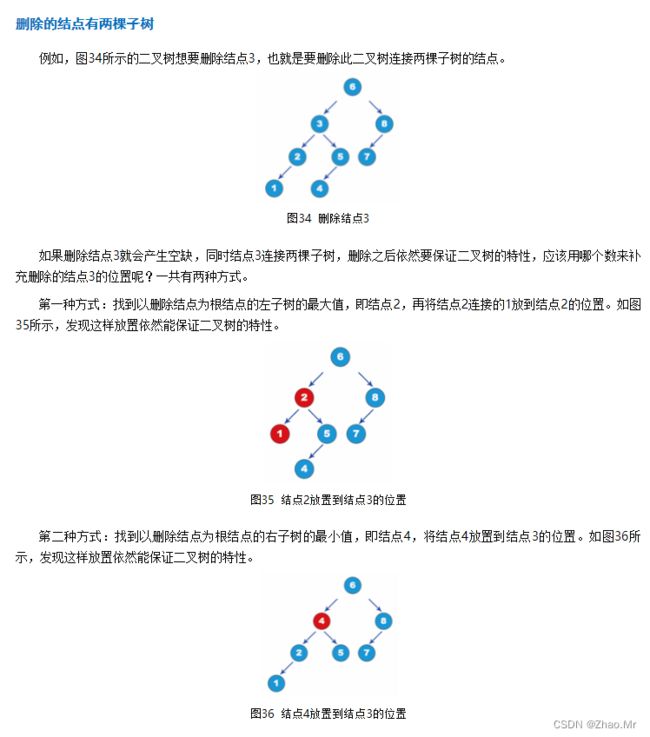
025.【树形结构算法】
1. 树的定义
树形结构是由n个元素组成的有限集合,如果n=0,那么就称为空树;如果n>0,树形结构应该满足以下条件:
-
有一个特定的结点,称为根结点或根。
-
除根结点外,其余结点被分成m(m≥0)个互不相交的有限集合,而每个子集又都是一棵树(称为原树的子树)。
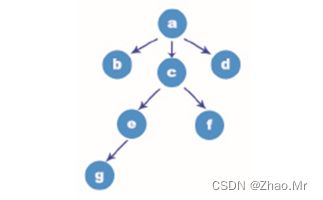
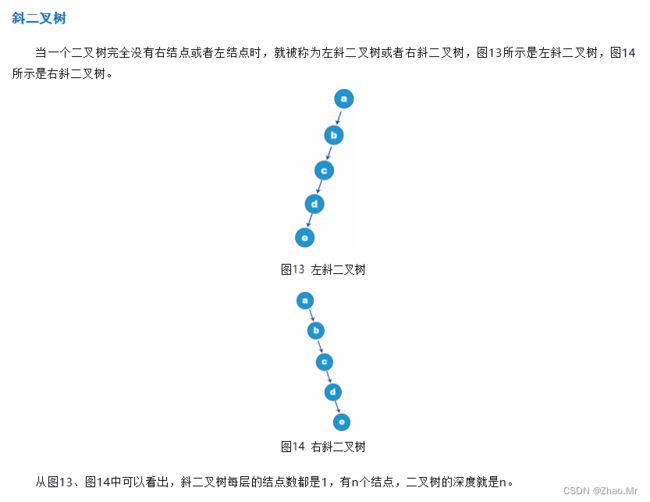
在介绍树形结构的条件时,提到了一个特殊的结点(根)。所示的树形结构的根就是结点a,就像树一样,树木要想长出茂密的枝条和叶子,就离不开树根。树形结构的形成也离不开根结点,只不过树是向上生长,而树形结构是从根往下描绘。根结点上面再也没有结点。
除了a这个根结点,图中的树形结构还有结点b,c,d,e,f,g,它们的共同点是不论是结点上面还是结点下面,至少都会存在1个与之连接的结点。并且为了能够结束树形结构,必须保证有一些无后续的结点,结点b,d,f,g。否则,就会变成一个无限的树形结构。
-
结点:“蓝色球”就被称为结点。
-
子树:以某个结点的子结点为根构成的树,称为该结点的子树。a结点它的子结点是c,以c为根构成的树,称为结点a的子树。类似于生活中的树的分叉上的树枝和叶子。
-
分支:各结点之间的关系,类似于生活中的树枝。
-
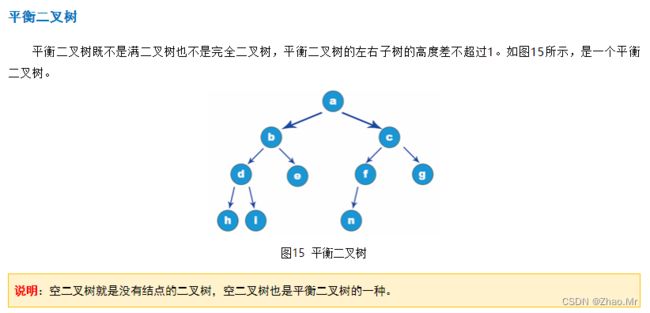
度:结点拥有的子树的个数称为该结点的度。结点a它的下一层(后继)有b,c,d这3个结点,因此结点a的度是3。
-
父结点:每个结点的上一层(前驱)结点,结点e它的父结点是c,结点c的父结点是a。
-
根结点:没有上一层(前驱)结点,一个树形结构只有一个根结点,结点a就是根结点。
-
子结点:某个结点的下一层(后继)结点,结点e,f 就是结点c的子结点。
-
叶子结点:没有下一层(后继)结点,称为叶子结点。叶子结点的度是0。结点b,g,f,g,就是叶子结点。
-
树的度:树中所有结点最大的度,称为树的度。a的度是3,c的度是2,e的度是1,最大的度是3,因此整个树形结构的度是3。
-
层次(层号):树中所有结点的度之和再加1。图所示的层次为:3×1+2×1+1×1+1=7,因此这个树形结构的层次是7
-
兄弟结点:拥有同一个父结点的结点称为兄弟结点。b、c、d就是兄弟结点。
-
深度:树中结点所处的最大层次,称为树的深度。树形结构一共有4层,它的深度就是4。
-
森林:互补相交的树的集合称为森林。类似于生活中很多大树便构成森林
2. 什么是二叉树
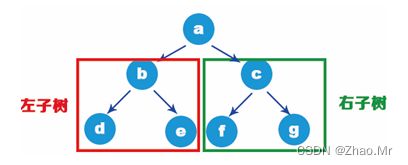
二叉树依然是树形结构。但是二叉树还有一个条件:它的每个结点都有两个分支,左侧分支称为“左子树”;右侧分支称为“右子树”,因此二叉树的最大的度就是2。
3. 二叉树操作
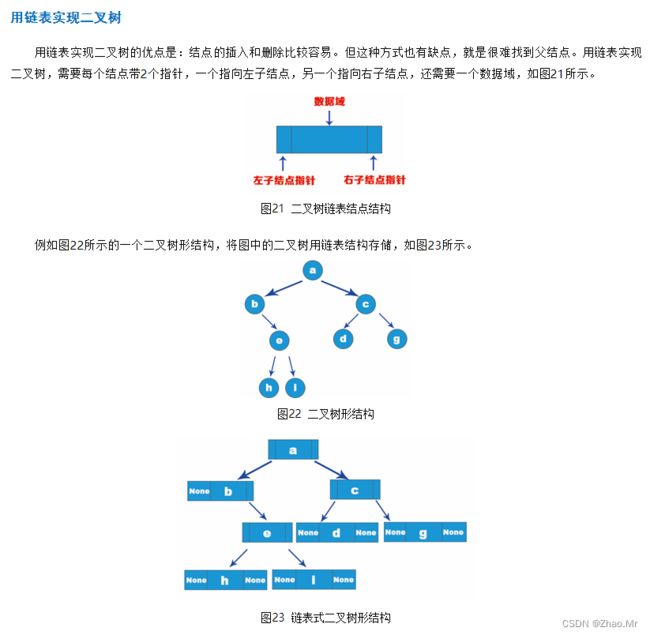
二叉树和其他数据结构一样,需要存储在内存中,二叉树存储有两种方式,一种是用数组方式存储,另一种是用链表方式存储。
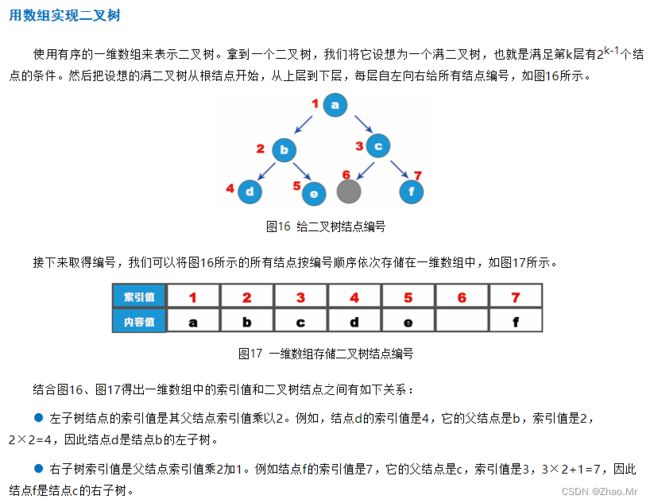
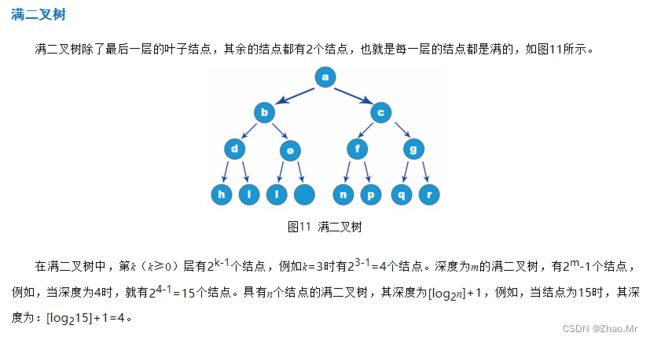
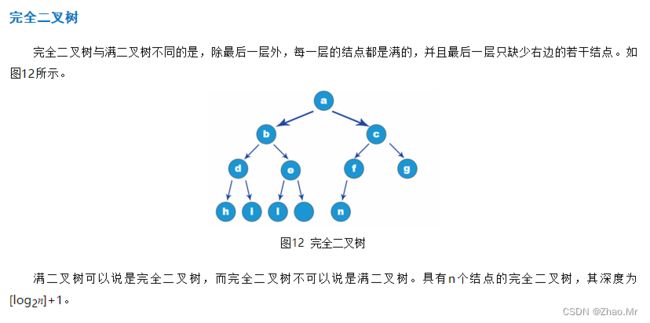
设计一个程序,用户输入数组内容,运行程序之后,按照“满二叉树”输出内容。具体代码如下:
"""
功能:用数组创建二叉树
参数:tree_array:存放二叉树数组
data:数据
length:长度
"""
def Binary_tree_create(tree_array, data, length):
for i in range(1, length):
index = 1 # 索引值初始化
while tree_array[index] != 0:
if data[i] > tree_array[index]: # 如果数组内的值大于树根,则往右子树比较
index = index * 2 + 1
else: # 如果数组内的值小于或等于树根,则往左子树比较
index = index * 2
tree_array[index] = data[i] # 把数组值放入二叉树
length = 9 # 长度为9
data = [0,3,2,6,7,4,5,1,9] # 原始数组
tree_array = [0] * 16 # 存放二叉树数组
print('原始数组内容:')
for i in range(length):
print('%2d ' % data[i], end='')
print('')
Binary_tree_create(tree_array, data, 9)
print('二叉树内容:')
for i in range(1, 16):
print('%2d ' % tree_array[i], end='')
print()
将0去掉之后,就是这个程序要实现的二叉树。
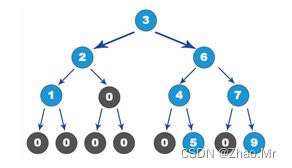
用数组实现二叉树的优点是:对于任意结点都很容易找到父结点、子结点和兄弟结点。如果是斜二叉树,该方法可能会占用大量空间,造成空间浪费。因此对于结点分布不均匀的二叉树来说,则用数组实现二叉树的方式会使效率降低,而且在删除和插入结点时,也不方便操作。在实际应用中,一般还是用链表来实现这样的二叉树。
class tree:
def __init__(self):
self.data=0 # 数据域
self.left=None # 左子结点指针
self.right=None # 右子结点指针
用链表方式建立二叉树的Python算法如下:
"""
功能:创建二叉树
参数:root:表示根结点
value:保存的值
"""
def creat_tree(root,value):
new_node=tree() # 创建树结点
new_node.data=value # 数据域
new_node.left=None # 左子树
new_node.right = None # 右子树
if root==None: # 如果根结点是空,这种情况就是空二叉树
root=new_node # 直接将根结点给新树
return root # 返回根结点
else:
current=root # 当前结点
while current!=None:
backup=current
if current.data>value: # 大于保存数值
current=current.left # 放在左子树
else: # 否则
current=current.right # 放在右子树
if backup.data>value:
backup.left=new_nod # 将数据左子树放在新树中
else:
backup.right=new_node # 将数据右子树放在新树中
return root
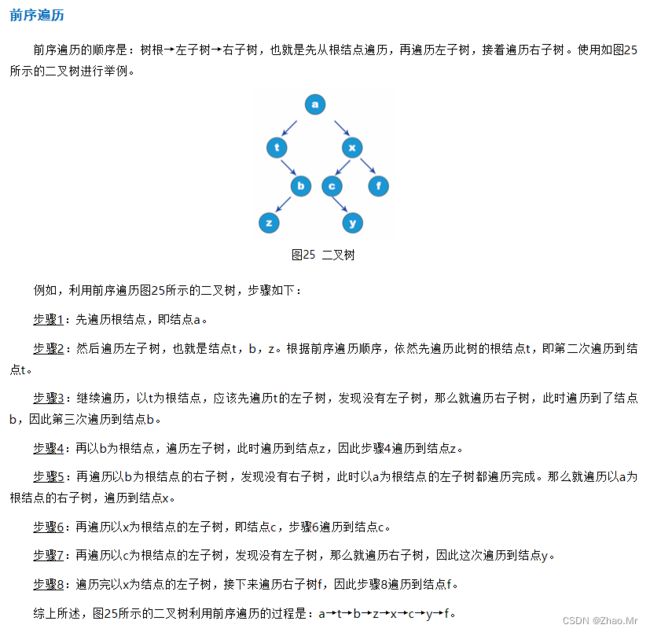
可以使用递归算法来实现上述步骤,因此使用Python代码实现前序遍历的算法如下:
def preorder(self,tree): # 前序遍历,tree是树结点
if tree == None: # 判断是空子树
return
# 当不为空子树时,先打印根结点,再打印左结点,最后打印右结点
print(tree.data)
self.preorder(tree.left)
self.preorder(tree.right)

可以使用递归算法来实现上述步骤,因此使用Python代码实现中序遍历的算法如下:
def inorder(self,tree): # 中序遍历,tree是树结点
if tree == None: # 判断是空子树
return
# 当不为空子树时,先打印左结点,再打印根结点,后打印右结点
self.inorder(tree.left)
print(tree.data)
self.inorder(tree.right)

可以使用递归算法来实现上述步骤,因此使用Python代码实现后序遍历的算法如下:
def postorder(self,tree): # 后序遍历,tree是树结点
if tree == None: # 判断是空子树
return
# 当不为空子树时,先打印左结点,再打印右结点,后打印根结点
self.postorder(tree.left)
self.postorder(tree.right)
print(tree.data)
先创建一个二叉树,即结点内容用a,x,c,t,b,f,y,z来表示,分别用先序遍历、中序遍历、后序遍历,按顺序输出此二叉树各个结点。具体代码如下:
class tree(object): # 创建树结点
def __init__(self, data=None, left=None, right=None): # 结点位置
self.data = data # 数据域
self.left = left # 左子树
self.right = right # 右子树
class BinaryTree(object): # 创建二叉树
def __init__(self, root=None): # 初始化
self.root = root
def is_empty(self): # 判断是否为空
return self.root == None
def preorder(self,tree): # 前序遍历
if tree == None: # 判断是空子树
return
# 当不为空子树时,先打印根结点,再打印左结点,后打印右结点
print(tree.data)
self.preorder(tree.left)
self.preorder(tree.right)
def inorder(self,tree): # 中序遍历
if tree == None: # 判断是空子树
return
# 当不为空子树时,先打印左结点,再打印根结点,后打印右结点
self.inorder(tree.left)
print(tree.data)
self.inorder(tree.right)
def postorder(self,tree): # 后序遍历
if tree == None: # 判断是空子树
return
# 当不为空子树时,先打印左结点,再打印右结点,后打印根结点
self.postorder(tree.left)
self.postorder(tree.right)
print(tree.data)
n1 = tree(data="z") # 二叉树结点z
n2 = tree(data="y") # 二叉树结点y
n3 = tree(data="f") # 二叉树结点f
n4 = tree(data="b", left=n1, right=None) # 二叉树结点b,左子树为z,无右子树
n5 = tree(data="t", left=None, right=n4) # 二叉树结点t,无左子树为,右子树为b
n6 = tree(data="c", left=None, right=n2) # 二叉树结点c,无左子树为,右子树为y
n7 = tree(data="x", left=n6, right=n3) # 二叉树结点x,左子树为c,右子树为f
root = tree(data="a", left=n5, right=n7) # 根结点a,左子树为t,右子树为x
ct = BinaryTree(root) # 创建二叉树
print('先序遍历')
ct.preorder(ct.root) # 输出前序遍历二叉树结果
print('中序遍历')
ct.inorder(ct.root) # 输出中序遍历二叉树结果
print('后序遍历')
ct.postorder(ct.root) # 输出后序遍历二叉树结果
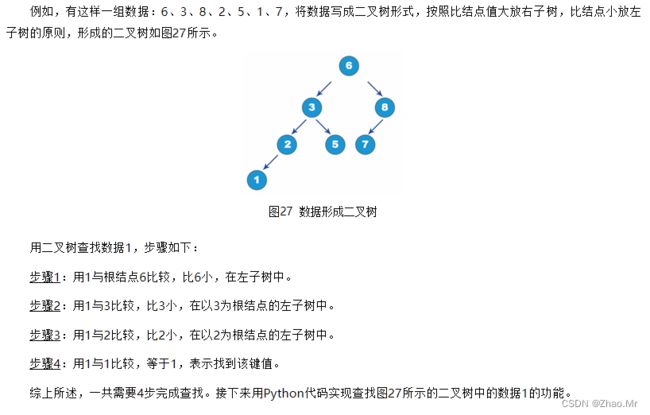
二叉树在建立过程中,是根据“左子树<树根<右子树”的原则建立的,因此只需从根结点开始比较键值就可以。如果键值比树根大就向右子树查找,如果键值比树根小就向左子树查找,直到键值相等就找到要查找的值。
用Python代码实现的二叉树查找算法如下:
def search(p,val): # 查找二叉树中某个值
while True: # 循环查找
if p==None: # 没找到就返回None
return None
if p.data==val: # 查找值等于结点值
return p
elif val<p.data : # 查找值小于结点值
ptr=p.left # 向左子树查找
else: # 否则
ptr=p.right # 向右子树查找
class tree:
def __init__(self):
self.data=0 # 数据域
self.left=None # 左子结点指针
self.right=None # 右子结点指针
"""
功能:创建二叉树
参数:root:表示根结点
value:保存的值
"""
def creat_tree(root,value):
new_node=tree() # 创建树结点
new_node.data=value # 数据域
new_node.left=None # 左子树
new_node.right = None # 右子树
if root==None: # 如果根结点是空,这种情况就是空二叉树
root=new_node # 直接将根结点给新树
return root # 返回根结点
else:
current=root # 当前结点
while current!=None:
backup=current
if current.data>value: # 大于保存数值
current=current.left # 放在左子树
else: # 否则
current=current.right # 放在右子树
if backup.data>value:
backup.left=new_node # 将数据左子树放在新树中
else:
backup.right=new_node # 将数据右子树放在新树中
return root
def search(p,val): # 查找二叉树中的某个值
i=1
while True: # 循环查找
if p==None: # 没找到就返回None
return None
if p.data==val: # 查找值等于结点值
print("共计查找 ",i,"次")
return p
elif val<p.data : # 查找值小于结点值
p=p.left # 向左子树查找
else: # 否则
p=p.right # 向右子树查找
i+=1 # 查找次数加1
arr=[6,3,8,2,5,1,7]
p=None
print('数据内容是')
for i in range(7):
p=creat_tree(p,arr[i]) # 建立二叉树
print('%2d ' %arr[i],end='')
print()
data=int(input('请输入查找值:'))
if search(p,data) !=None : # 在二叉树中查找
print("您要找的值",data,"找到了^_^" )
else:
print("您要找的值没找到^ ^")
二叉树结点插入的情况和查找类似,如果要插入的结点已经在二叉树中,就不必插入了;如果要插入的结点不在二叉树中,就利用创建函数将数据插入到二叉树中,插入之后的二叉树依然保持左子树比根结点小,右子树比根结点大的特性。
利用Python代码实现二叉树结点的插入算法如下:
if search(ptr,data)!=None: # 在二叉树中查找
print("真巧,二叉树中已经有你输入的结点啦~")
else: # 不在二叉树中
ptr=creat_tree(ptr,data) # 调用创建函数将数据插入
inorder(ptr) # 输出插入之后的新的二叉树
给定一个二叉树内容为6,3,8,2,5,1,7,用户输入一个想要在此二叉树中插入的键值。成功插入后,最终用中序遍历输出此二叉树各个结点内容。具体代码如下:
class tree:
def __init__(self):
self.data=0 # 数据域
self.left=None # 左子结点指针
self.right=None # 右子结点指针
"""
功能:创建二叉树
参数:root:表示根结点
value:保存的值
"""
def creat_tree(root,value):
new_node=tree() # 创建树结点
new_node.data=value # 数据域
new_node.left=None # 左子树
new_node.right = None # 右子树
if root==None: # 如果根结点是空,这种情况就是空二叉树
root=new_node # 直接将根结点给新树
return root # 返回根结点
else:
current=root # 当前结点
while current!=None:
backup=current
if current.data>value: # 大于保存数值
current=current.left # 放在左子树
else: # 否则
current=current.right # 放在右子树
if backup.data>value:
backup.left=new_node # 将数据左子树放在新树中
else:
backup.right=new_node # 将数据右子树放在新树中
return root
def search(p,val): # 查找二叉树中某个值
while True: # 循环查找
if p==None: # 没找到就返回None
return None
if p.data==val: # 查找值等于结点值
return p
elif val<p.data : # 查找值小于结点值
p=p.left # 向左子树查找
else: # 否则
p=p.right # 向右子树查找
def inorder(ptr): # 中序遍历子程序
if ptr!=None:
inorder(ptr.left)
print('%2d ' %ptr.data, end='')
inorder(ptr.right)
arr=[6,3,8,2,5,1,7]
ptr=None
print("数据内容是:")
for i in range(7):
ptr=creat_tree(ptr,arr[i]) # 建立二叉树
print('%2d ' %arr[i],end='')
print()
data=int(input('请输入要插入的键值:'))
if search(ptr,data)!=None: # 在二叉树中查找
print('真巧,二叉树中已经有你输入的结点啦~')
else:
print("插入数据后中序遍历输出结果为:")
ptr=creat_tree(ptr,data) # 将数据插入树中
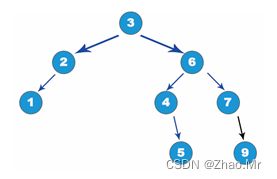
inorder(ptr) # 中序遍历输出各数据
插入数据4之后的二叉树如图所示。