时序预测 | MATLAB实现SO-ELM蛇群算法优化极限学习机时间序列预测

时序预测 | MATLAB实现SO-ELM蛇群算法优化极限学习机时间序列预测

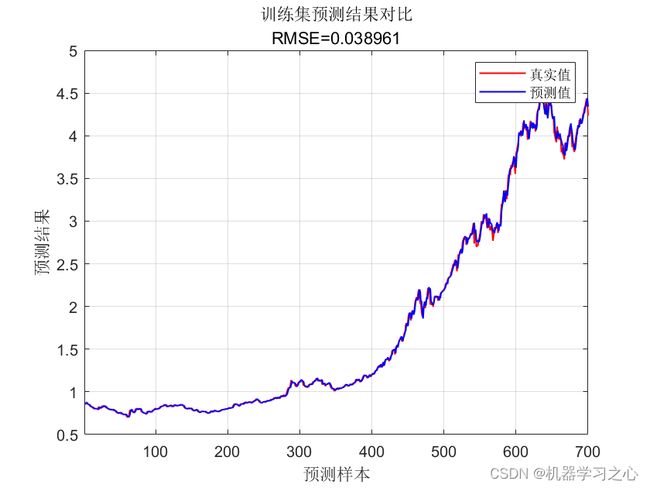
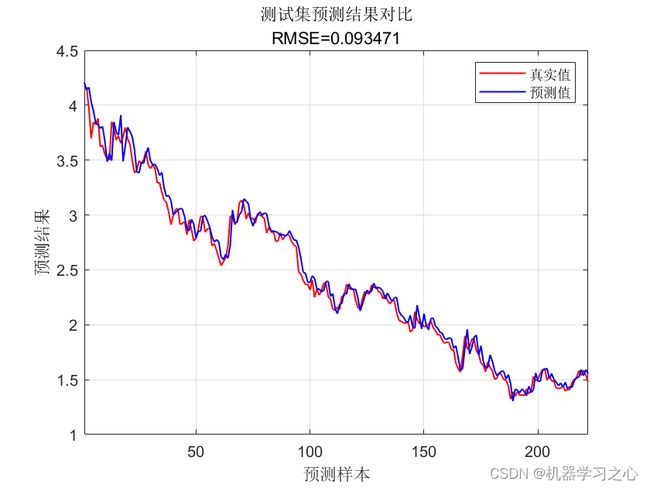
效果一览

基本介绍

Matlab实现SO-ELM蛇群算法优化极限学习机时间序列预测
1.data为单变量时间序列数据集，运行环境Matlab2018b及以上。
2.运行主程序文件，其余为函数文件，无需运行。
3.命令窗口输出MAE、MBE和R2，可在下载区获取数据和程序内容。
4.Matlab蛇群算法优化极限学习机(SO-ELM)时间序列预测，优化参数为权值和阈值。

程序设计

• 完整程序和数据下载方式1(资源处直接下载)：MATLAB实现SO-ELM蛇群算法优化极限学习机时间序列预测

• 完整程序和数据下载方式2(订阅《ELM极限学习机》专栏，同时可阅读《ELM极限学习机》专栏收录的所有内容，数据订阅后私信我获取)：MATLAB实现SO-ELM蛇群算法优化极限学习机时间序列预测

• 完整程序和数据下载方式3(订阅《智能学习》专栏，同时获取《智能学习》专栏收录程序5份，数据订阅后私信我获取)：MATLAB实现SO-ELM蛇群算法优化极限学习机时间序列预测

• SO.m

function [Best_pos, Best_score,curve] = SO(pop,Max_iter,lb,ub,dim,fobj)
%initial 
vec_flag=[1,-1];
Threshold=0.25;
Thresold2= 0.6;
C1=0.5;
C2=.05;
C3=2;
% if(max(size(ub)) == 1)
%    ub = ub.*ones(1,dim);
%    lb = lb.*ones(1,dim);
% end
X=initialization(pop,dim,ub,lb)
%X=lb+rand(pop,dim)*(ub-lb);
for i=1:pop
 fitness(i)=feval(fobj,X(i,:));   
end
[GYbest, gbest] = min(fitness);
Best_pos = X(gbest,:);
%Diving the swarm into two equal groups males and females
Nm=round(pop/2);%eq.(2&3)
Nf=pop-Nm;
Xm=X(1:Nm,:);
Xf=X(Nm+1:pop,:);
fitness_m=fitness(1:Nm);
fitness_f=fitness(Nm+1:pop);
[fitnessBest_m, gbest1] = min(fitness_m);
Xbest_m = Xm(gbest1,:);
[fitnessBest_f, gbest2] = min(fitness_f);
Xbest_f = Xf(gbest2,:);
for t = 1:Max_iter
    Temp=exp(-((t)/Max_iter));  %eq.(4)
  Q=C1*exp(((t-Max_iter)/(Max_iter)));%eq.(5)
    if Q>1        Q=1;    end
    % Exploration Phase (no Food)
if Q<Threshold
    for i=1:Nm
        for j=1:1:dim
            rand_leader_index = floor(Nm*rand()+1);
            X_randm = Xm(rand_leader_index, :);
            flag_index = floor(2*rand()+1);
            Flag=vec_flag(flag_index);
            Am=exp(-fitness_m(rand_leader_index)/(fitness_m(i)+eps));%eq.(7)
            Xnewm(i,:)=X_randm(j)+Flag*C2*Am*((ub-lb)*rand+lb);%eq.(6)
        end
    end
    for i=1:Nf
        for j=1:1:dim
            rand_leader_index = floor(Nf*rand()+1);
            X_randf = Xf(rand_leader_index, :);
            flag_index = floor(2*rand()+1);
            Flag=vec_flag(flag_index);
            Af=exp(-fitness_f(rand_leader_index)/(fitness_f(i)+eps));%eq.(9)
            Xnewf(i,:)=X_randf(j)+Flag*C2*Af*((ub-lb)*rand+lb);%eq.(8)
        end
    end
else %Exploitation Phase (Food Exists)
    if Temp>Thresold2  %hot
        for i=1:Nm
            flag_index = floor(2*rand()+1);
            Flag=vec_flag(flag_index);
            for j=1:1:dim
                Xnewm(i,:)=Best_pos(j)+C3*Flag*Temp*rand*(Best_pos(j)-Xm(i,j));%eq.(10)
            end
        end
        for i=1:Nf
            flag_index = floor(2*rand()+1);
            Flag=vec_flag(flag_index);
            for j=1:1:dim
                Xnewf(i,:)=Best_pos(j)+Flag*C3*Temp*rand*(Best_pos(j)-Xf(i,j));%eq.(10)
            end
        end
    else %cold
        if rand>0.6 %fight
            for i=1:Nm
                for j=1:1:dim
                    FM=exp(-(fitnessBest_f)/(fitness_m(i)+eps));%eq.(13)
                    Xnewm(i,:)=Xm(i,j) +C3*FM*rand*(Q*Xbest_f(j)-Xm(i,j));%eq.(11)
                    
                end
            end
            for i=1:Nf
                for j=1:1:dim
                    FF=exp(-(fitnessBest_m)/(fitness_f(i)+eps));%eq.(14)
                    Xnewf(i,:)=Xf(i,j)+C3*FF*rand*(Q*Xbest_m(j)-Xf(i,j));%eq.(12)
                end
            end
        else%mating
            for i=1:Nm
                for j=1:1:dim
                    Mm=exp(-fitness_f(i)/(fitness_m(i)+eps));%eq.(17)
                    Xnewm(i,:)=Xm(i,j) +C3*rand*Mm*(Q*Xf(i,j)-Xm(i,j));%eq.(15
                end
            end
            for i=1:Nf
                for j=1:1:dim
                    Mf=exp(-fitness_m(i)/(fitness_f(i)+eps));%eq.(18)
                    Xnewf(i,:)=Xf(i,j) +C3*rand*Mf*(Q*Xm(i,j)-Xf(i,j));%eq.(16)
                end
            end
            flag_index = floor(2*rand()+1);
            egg=vec_flag(flag_index);
            if egg==1;
                [GYworst, gworst] = max(fitness_m);
                Xnewm(gworst,:)=lb+rand*(ub-lb);%eq.(19)
                [GYworst, gworst] = max(fitness_f);
                Xnewf(gworst,:)=lb+rand*(ub-lb);%eq.(20)
            end
        end
    end
end
    for j=1:Nm
         Flag4ub=Xnewm(j,:)>ub;
         Flag4lb=Xnewm(j,:)<lb;
        Xnewm(j,:)=(Xnewm(j,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
        y = feval(fobj,Xnewm(j,:));
        if y<fitness_m(j)
            fitness_m(j)=y;
            Xm(j,:)= Xnewm(j,:);
        end
    end
    
    [Ybest1,gbest1] = min(fitness_m);
    
    for j=1:Nf
         Flag4ub=Xnewf(j,:)>ub;
         Flag4lb=Xnewf(j,:)<lb;
        Xnewf(j,:)=(Xnewf(j,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
        y = feval(fobj,Xnewf(j,:));
        if y<fitness_f(j)
            fitness_f(j)=y;
            Xf(j,:)= Xnewf(j,:);
        end
    end
    
    [Ybest2,gbest2] = min(fitness_f);
    
    if Ybest1<fitnessBest_m
        Xbest_m = Xm(gbest1,:);
        fitnessBest_m=Ybest1;
    end
    if Ybest2<fitnessBest_f
        Xbest_f = Xf(gbest2,:);
        fitnessBest_f=Ybest2;
        
    end
    if Ybest1<Ybest2
        curve(t)=min(Ybest1);
    else
        curve(t)=min(Ybest2);
        
    end
    if fitnessBest_m<fitnessBest_f
        GYbest=fitnessBest_m;
        Best_pos=Xbest_m;
    else
        GYbest=fitnessBest_f;
        Best_pos=Xbest_f;
    end
    
end
Best_score = GYbest;
end

• initialization.m

function Positions = initialization(SearchAgents_no, dim, ub, lb)

%%  初始化

%%  待优化参数个数
Boundary_no = size(ub, 2); 

%%  若待优化参数个数为1
if Boundary_no == 1
    Positions = rand(SearchAgents_no, dim) .* (ub - lb) + lb;
end

%%  如果存在多个输入边界个数
if Boundary_no > 1
    for i = 1 : dim
        ub_i = ub(i);
        lb_i = lb(i);
        Positions(:, i) = rand(SearchAgents_no, 1) .* (ub_i - lb_i) + lb_i;
    end
end

学习总结

极限学习机，为人工智能机器学习领域中的一种人工神神经网络模型，是一种求解单隐层前馈神经网路的学习演算法。极限学习机是用于分类、回归、聚类、稀疏逼近、压缩和特征学习的前馈神经网络，具有单层或多层隐层节点，其中隐层节点的参数（不仅仅是将输入连接到隐层节点的权重）不需要被调整。这些隐层节点可以随机分配并且不必再更新（即它们是随机投影但具有非线性变换），或者可以从其祖先继承下来而不被更改。在大多数情况下，隐层节点的输出权重通常是一步学习的，这本质上相当于学习一个线性模型。

参考资料

[1] G.-B. Huang, Q.-Y. Zhu, and C.-K. Siew, “Extreme learning machine: A new learning scheme of feedforward neural networks,” in Proc. Int. Joint Conf. Neural Networks, July 2004, vol. 2, pp. 985–990.
[2] https://blog.csdn.net/kjm13182345320/article/details/127361354