西安石油大学2023年第三届里奇杯编程大赛(初赛)
官方题解地址1v7w (郭毅佬!):https://www.cnblogs.com/1v7w/p/17437203.html
A 签到
描述
你说得对,但是 “ 里奇杯 ” 是西安石油大学计算机协会举办的程序设计竞赛,比赛旨在激发同学们学习程序设计的热情,提高编程能力,调动编程的兴趣和积极性,在这里,你将扮演名为“参赛选手”的神秘角色,展示分析问题、解决问题和动手编程的能力,培养创新思维,开拓视野,邂逅志趣相投的同伴,同时,逐步发掘 “ 算法 ” 的魅力。
输入
无
输出
输出一行字符串Hello Liqi contest
输入样例 1 无
输出样例 1 Hello Liqi contest
#include 其他方法(推荐去leetcode或者洛谷去看各路神仙的输出方法,直接劝退萌新doge)
以下是几种在C++中输出"Hello Liqi contest"的方法:
1. 使用cout语句:
```
#include B 挂科
描述
老师希望同学们都能取得一个好成绩,所以每次成绩出来,老师去统计一下有多少同学挂科了。现在老师安排让1v7w去统计,但他数数不太行,请你给写个程序帮他统计一下。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6SszeRBt-1687177451108)(2023-06-04-21-00-48.png)]
分析思路:
在这个示例中,我们先定义三个变量,分别表示学生数量、及格线和学生成绩数组。然后使用scanf函数从标准输入中读取n和p的值,再使用for循环读取n个学生的成绩到数组a中。
最后,使用一个for循环遍历所有学生成绩,输出及格的学生成绩。
#include 官方题解:
//这段代码实现了统计成绩低于及格线的学生数量。
//首先,我们定义了一个常量N表示数组a的最大长度。
//然后,使用scanf函数从标准输入中读取n和p的值,
//并使用for循环遍历n个学生的成绩,并把它们存储在数组a中。
//接下来,我们定义一个变量res,用于记录成绩低于及格线的学生数量。
//使用一个循环遍历数组a,如果某个学生成绩小于及格线,则将res的值加一。
最后,输出成绩低于及格线的学生数量res即可。
#include C 送外卖
暑假1v7w想要赚钱,于是就进入了美团大厂,成为了一名骑手。
这一天他抢到了 n 个订单,这些订单的目的地都在宝鸡钢管路上(可以看做在一条坐标轴上),第 i 个订单的目的地的位置是 。
帮1v7w找一下,他最少走多长的距离就能够把外卖全部送完?这里他可以从任意一点开始送外卖,并从任意一点结束送外卖。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ErPiyk80-1687177451111)(2023-06-04-21-15-21.png)]
经过论证,可以发现,沿着坐标轴,从左到右一口气送完外卖是最佳方案。故将求出 a的最大值与最小值后直接相减即可。
官方题解:
这段代码实现了求取n个数中最大值和最小值的差。
在main函数中,我们首先使用scanf函数读取变量n的值。接着,我们定义了两个变量minv和maxv,分别表示当前遍历到数列中出现的最小值和最大值(初始值需要设得足够大或小)。使用一个循环遍历输入的n个数,更新minv和maxv的值。最后,输出maxv和minv的差就是答案。
在代码中还有一部分注释掉了,这部分代码是用于多组数据的处理。如果输入有多组数据,需要将其放在while(t–)循环内部来解决。
#include 经过论证,可以发现,沿着坐标轴,从左到右一口气送完外卖是最佳方案。故将求出 a的最大值与最小值后直接相减即可。
#include 首先,使用cin从标准输入中读取变量n的值,并用一个for循环遍历将后面n个数读入数组a中。
然后,使用STL库函数*max_element和*min_element分别求得a中的最大值和最小值,并依次赋值给maxv和minv。
最后,输出maxv和minv的差就是答案。
D 分弹珠
描述
你和你的好朋友在放学的路上捡到了N颗弹珠(每颗弹珠都是一模一样的),看到四下无人,你们俩打算将这些弹珠分掉,请问在确保每个人都能分到的情况下共有多少种分配方式?
输入
第一行包含一个整数 1≤ ≤15
N(1≤N≤15),表示弹珠的总数。
输出
输出一个整数,表示分配方式的总数。
官方题解
每个弹珠都一模一样,故弹珠分配方案的不同只有每个人分的的弹珠多少。
每个人能分得的弹珠数量区间是 [1,n−1] ,故方案数为 n−1。这里直接把弹珠数量为 1的情况(没有合理的分配方案)也涵盖了。
#include E.加倍整数
描述
我们将一个位数为偶数且前半部分与后半部分相同的数称为加倍整数,例如:
11
,
1212
,
123123
11,1212,123123 等。
给你一个整数 N ,请问从 1 到 N 有多少个加倍整数?
输入
第一行包含一个整数 1 <= N <= 10^12
输出
输出一行,表示加倍整数的个数。
官方题解
比起判断某个数是否为加倍整数,不如直接构造加倍整数出来,判断他与 n的关系。
#include 这段代码实现了一个简单的功能:计算小于等于n的加倍整数的个数。
代码中首先定义了常量N为1e6+10,并定义了变量n和函数bianshen(x)。函数bianshen(x)用于将x变为xx的加倍整数,即将x的字符串形式重复一次后再转为整数。
在主函数中,首先读入n的值,然后使用for循环遍历所有小于N的正整数i,计算i的加倍整数bianshen(i)。如果bianshen(i)小于等于n,则将计数器res加1。
最后输出res的值,即小于等于n的加倍整数的数量。
该代码使用了C++11的标准库,包括iostream、algorithm、queue、set、map、vector、string等头文件,以及using关键字定义了ll和pii等类型别名,方便了代码编写。代码的时间复杂度为O(NlogN),其中N为1e6,可通过本题。
个人题解
加倍整数指的是一个正整数,如果将它的最高位复制一次接在它的最低位之后,得到的新数是原数的两倍。例如,22是一个加倍整数,因为它的最高位是2,将2复制一次得到新数122,而122是22的两倍。
以下是一段C++代码,可用于判断一个正整数是否为加倍整数:
#include
#include
using namespace std;
bool isDouble(int n)
{
bool flag = false;
string str = to_string(n); // 将整数转为字符串
int len = str.length();
if (str[0] == str[len-1]) // 判断最高位和最低位是否相等
{
flag = true;
for (int i = 1; i < len/2; i++) // 判断其他位是否相等
{
if (str[i] != str[i+len/2])
{
flag = false;
break;
}
}
}
return flag;
}
int main()
{
int n;
cout << "请输入一个正整数:";
cin >> n;
if (isDouble(n))
cout << n << "是加倍整数。" << endl;
else
cout << n << "不是加倍整数。" << endl;
return 0;
}
该代码首先将输入的正整数转换为字符串,然后判断最高位和最低位是否相等,如果相等再判断其他位是否相等,最后返回判断结果。
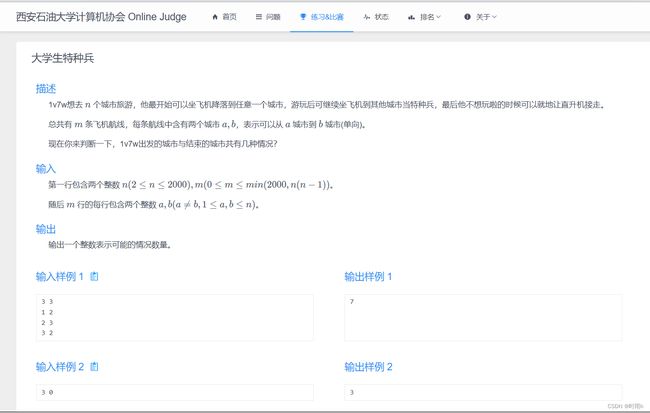
大学生特种兵
官方题解
假如有一段路程为 1−>2−>4−>5−>3,则他旅行的起点可以为其中的任意一个,终点为起点后的任意一个。故我们可以枚举起点,然后搜索他能够去到哪些终点。
#include DFS
DFS(Depth First Search)即深度优先搜索,是一种常见的图遍历算法。在C++中,可以使用递归或栈来实现DFS算法。
具体实现方式如下:
- 递归
递归实现DFS算法比较简单,代码如下:
const int N = 100010;
vector g[N]; // 图的邻接表表示
bool vis[N]; // 记录每个节点是否被访问过
// 从节点u开始进行深度优先遍历
void dfs(int u) {
vis[u] = true; // 标记节点u为已访问
cout << u << " "; // 输出节点u
for (auto v : g[u]) { // 遍历节点u的出边
if (!vis[v]) { // 如果节点v未被访问过
dfs(v); // 递归遍历节点v
}
}
}
int main() {
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1); // 从节点1开始进行深度优先遍历
return 0;
}
在这段代码中,dfs函数代表从节点u开始进行深度优先遍历。首先标记节点u为已访问,然后输出节点u,最后遍历节点u的所有出边。如果一个出边指向的节点v未被访问过,则递归调用dfs(v)进行遍历。
2. 栈
非递归实现DFS算法需要手动维护一个栈来存储节点信息,代码如下:
const int N = 100010;
vector g[N]; // 图的邻接表表示
bool vis[N]; // 记录每个节点是否被访问过
// 从节点u开始进行深度优先遍历
void dfs(int u) {
stack stk; // 定义一个栈
stk.push(u); // 将起始节点u入栈
while (!stk.empty()) { // 当栈不为空时
int t = stk.top();
stk.pop();
if (!vis[t]) { // 如果节点t未被访问过
vis[t] = true; // 标记节点t为已访问
cout << t << " "; // 输出节点t
for (auto v : g[t]) { // 遍历节点t的出边
if (!vis[v]) { // 如果节点v未被访问过
stk.push(v); // 将节点v入栈
}
}
}
}
}
int main() {
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1); // 从节点1开始进行深度优先遍历
return 0;
}
在这段代码中,dfs函数代表从节点u开始进行深度优先遍历。我们使用一个栈来存储节点信息,将起始节点u入栈。当栈不为空时,取出栈顶节点t。如果节点t未被访问过,则标记节点t为已访问,输出节点t,遍历节点t的所有出边,将出边指向的未访问节点v入栈。
总结一下,DFS算法是一种非常常用的图遍历算法,递归实现简单,但是当图过大时有可能导致栈溢出。因此,我们可以使用非递归方法,手动维护一个栈来实现DFS遍历。在使用DFS遍历图时,要注意记录每个节点是否被访问过,避免重复访问。
不许6
官方题解
a=[1,2,3,4,5,7,8,9,10,11,12,13,14,15,17,18,…]。从这里可以发现这个数字世界就是一个使用数字 0,1,2,3,4,5,7,8,9的九进制。故我们将获取到的数字从十进制转换为九进制即可,注意把转换后的 [6,8]变为 [7,9]。
#include 根据题目描述,1v7w的数字世界中没有数字6,因此我们需要将所有数字中的6去掉,生成新的数字序列。
具体代码实现如下:
#include
#include
using namespace std;
vector a;
void generate() {
int x = 1;
while (x <= 1000000) {
if (x % 10 != 6 && x / 10 % 10 != 6) {
a.push_back(x);
}
x++;
}
}
int main() {
generate();
int k;
cin >> k;
if (k <= 0 || k > a.size()) {
cout << "Error" << endl;
} else {
cout << a[k - 1] << endl;
}
return 0;
}
首先,我们定义一个vector a来存储符合要求的数字序列,然后编写generate函数来生成这个序列。generate函数使用一个while循环来遍历所有小于等于1000000的正整数,将没有6的数字加入到a中。
在主函数中,我们读入一个整数k,判断其是否在a的下标范围之内。如果在范围之内,则输出a[k-1],即第k个符合要求的数字;否则输出"Error"。
该程序的时间复杂度是O(n),其中n是符合要求的数字个数,即小于等于1000000的去掉了含有数字6的数字个数,可以通过本题。
vector
在C++中,vector是一个非常常用的动态数组容器,它可以在运行时动态扩展大小,并且支持随机访问、在尾部添加元素、在尾部删除元素等操作。在使用vector时,需要包含头文件。
vector的定义方式如下:
vector v; // 定义一个空的vector容器
vector v(n); // 定义一个有n个元素的vector容器,每个元素都是0
vector v(n, m); // 定义一个有n个元素的vector容器,每个元素都是m
其中,n表示vector容器的大小,m表示初始值。可以通过v.size()来获取vector容器的大小,通过v[i]来访问第i个元素。
vector的常用操作如下:
- 在尾部添加元素
vector v;
v.push_back(1); // 在尾部添加元素1
v.push_back(2); // 在尾部添加元素2
- 在尾部删除元素
vector v = {1, 2, 3};
v.pop_back(); // 删除尾部元素3
v.pop_back(); // 删除尾部元素2
- 随机访问元素
vector v = {1, 2, 3};
cout << v[0] << endl; // 输出第一个元素1
cout << v[1] << endl; // 输出第二个元素2
cout << v[2] << endl; // 输出第三个元素3
- 清空vector
vector v = {1, 2, 3};
v.clear(); // 清空vector
- 遍历vector
vector v = {1, 2, 3};
for (int i = 0; i < v.size(); i++) {
cout << v[i] << " ";
}
cout << endl;
- 插入元素
vector v = {1, 2, 3};
v.insert(v.begin() + 1, 4); // 在第二个位置插入元素4
for (int i = 0; i < v.size(); i++) {
cout << v[i] << " ";
}
cout << endl;
以上是vector容器的常用操作,vector还支持很多其他的操作,如排序、查找、删除等,具体可以参考C++的官方文档。需要注意的是,当vector的元素个数超过当前容量时,vector会重新分配一个更大的内存块,并将原有元素复制到新内存块中,这可能导致性能问题。因此,在使用vector时,可以通过调用reserve函数来预分配容量,避免频繁的内存分配复制。