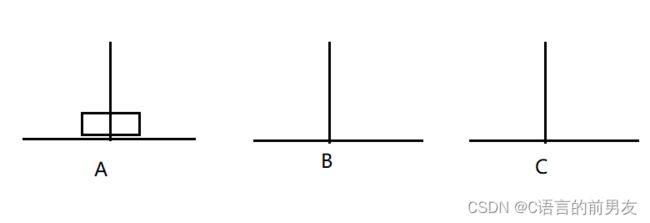深度理解递归，手撕经典递归问题（汉诺塔，青蛙跳台阶），保姆级教学。

目录

序言：

一.函数递归（ recursion）

二.递归的两个必要条件

三.递归小问题

（1）接受一个整型值（无符号），按照顺序打印它的每一位

（2）编写函数不允许创建临时变量，求字符串的长度（利用递归求解）

（3）求第n个斐波那契数。（不考虑溢出）

 提示：1. 许多问题是以递归的形式进行解释的，这只是因为它比非递归的形式更为清晰。2. 但是这些问题的迭代实现往往比递归实现效率更高，虽然代码的可读性稍微差些。3. 当一个问题相当复杂，难以用迭代实现时，此时递归实现的简洁性便可以补偿它所带来的运行时开销。

四.经典递归案例

1.汉诺塔

 2.青蛙跳台阶

最后：

---

序言：

今天来聊一聊递归，相信函数递归是不少小伙伴在学习编程路上遇到的一个拦路虎吧，今天带着大家一起把这个拦路虎干掉。相信小伙伴跟着我一起把递归深度解剖一遍，大家一定会内功大增。

一.函数递归（ recursion）

所谓递归就是一种程序调用自身的编程技巧。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。

递归的主要思考方式在于：把大事化小，小问题也是大问题的一个子问题，只要将子问题解决大问题也就迎刃而解。

二.递归的两个必要条件

（1）存在限制条件，当满足这个限制条件的时候，递归便不再继续。
（2）每次递归调用之后越来越接近这个限制条件。

注意：存在这两个条件递归不一定正确，但是不存在这两个条件，递归一定不正确。

三.递归小问题

（1）接受一个整型值（无符号），按照顺序打印它的每一位

  我们要想输出他的每一位，是不难的，直接用循环模10除10并将得到的数，存储到数组中，然后倒叙输出，就解决问题了。但是这里我们希望使用递归来解决问题。又该怎么理解呢?

  首先分析问题，我们需要正序打印每一位，我们可以先打印 123  加上单独 4 这样就把问题分成一个与原问题相似的规模较小的问题——正序打印 123 的每一位。那么正序打印 123 ，又可以分成先正序打印 12 再加上单独打印 3 ，以此类推，又可以把问题分形成正序打印 1 再加上正序打印 2 ，当只剩一位的时候自然也就没法差分了，就直接打印 1 。

上代码：

#include
void print(int num)
{
	//只有一位数直接打印
	if (num < 10)
	{
		printf("%d ", num);
	}
	//不止一位数
	else
	{
		//num/10,就是去除num的最后一位，打印num最后一位之前的每一位。
		print(num / 10);
		//加上单独打印num的最后一位。
		printf("%d ", num % 10);
	}
}
int main()
{
	int num = 0;
	scanf("%d", &num);
	print(num);
	return 0;
}

运行结果：

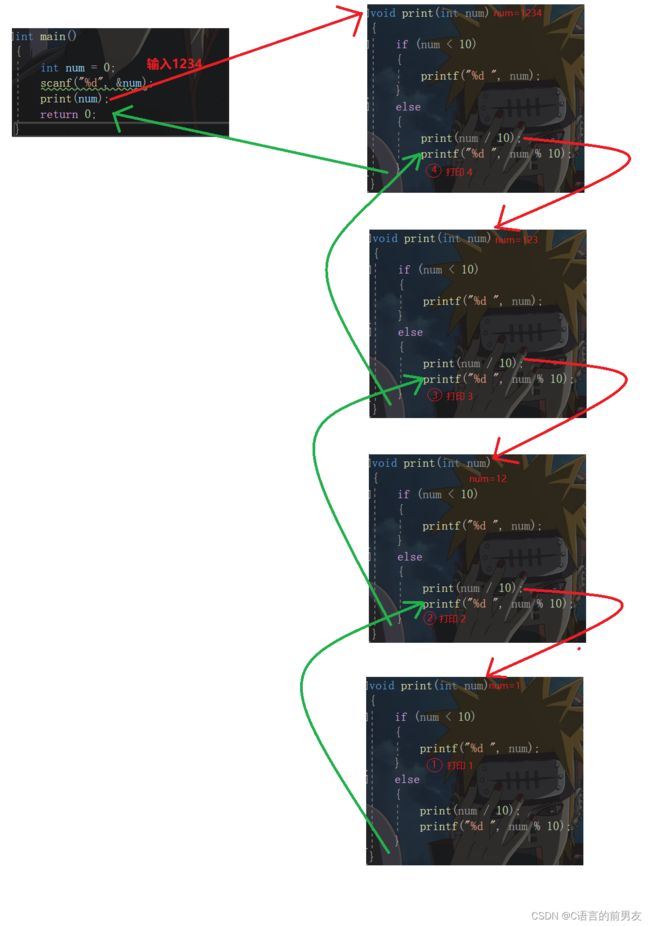
 递归函数展开图解

 

 这里图解中红色路线叫做递推，蓝色部分回归，这就是递归的展开思路。

但是这里还是要提醒大家，大家理解递归代码的时候，千万不要陷入一种惯性思维，就是见到递归就想着去坐进递归，一般递归都带着严谨且复杂的逻辑，我们是无法彻底走到底的。关键在于要利用递归这种大事化小的思维去整体理解递归。

（2）编写函数不允许创建临时变量，求字符串的长度（利用递归求解）

思路点拨：

这里先简单介绍一下，怎样求一个字符串的长度，再来看怎么用递归求解。

首先，C语言提供了一个求字符串长度的函数——strlen（  ）；我们知道字符串的结尾都会隐含一个字符' \0 ' ;这个 ' \0 '就是字符串的结束标志，所 strlen（ ）也是通过查找 ' \0 '来确定字符串长度。聊到这里我们也就可以尝试使用递归解决了。  

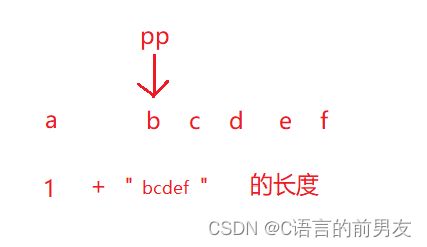
这里我们假如有一个字符串 char * p="abcdef";然后用另外一个指针表示我们的字符串，

 当我们的pp指针指向的字符不是' \0 ' 时，就代表字符串至少有一个字符，加上pp向后移动一位，代表的字符串的长度就是，总字符串的长度。

 

 所以代码就很简单了

#include
int Strlen(const char* str)
{
    //str指向的字符是'\0';就代表已经到达字符串的结尾，返回 0 
    if (*str == '\0')
    {
        return 0;
    }
    //str指向的字符不是'\0'; 就代表长度至少是 1，跳过这个字，
    //再加上后面的字符数就是，总长度了。
    else
    {
        return 1 + Strlen(str + 1);
    }

}
int main()
{
    char* p = "abcdef";
    int len = Strlen(p);
    printf("%d\n", len);
    return 0;
}

（3）求第n个斐波那契数。（不考虑溢出）

首先我们了解一下什么是斐波那契数，1 ，1 ，2 ，3，5，8，13，21，34，55 ........这样第一和第二个数是 1，从第三个数开始是，前面两个数的和。这就是斐波那契数列，我们称数列中的数是斐波那契数。这个规律显然易见，就可以写出一个表达式：

 代码：

#include
int fib(int n)
{
	if (n <= 2)
		return 1;
	else
		return fib(n - 1) + fib(n - 2);
}
int main()

{
	int n = 0;
	scanf("%d", &n);
	int num = fib(n);
	printf("第%d位斐波那契数是%d\n",n, num);
	return 0;
}

但是当我们算的位数比较大时就会计算非常慢，这就是因为，再用递归计算斐波那契数时，会产生大量重复的计算。

这里我们看一下，求第40位斐波那契数，第三位斐波那契数算了多少次：

#include
int count = 0;//全局变量
int fib(int n)
{
    if (n == 3)
        count++;
    if (n <= 2)
        return 1;
    else
        return fib(n - 1) + fib(n - 2);
}
int main()

{
    int n = 0;
    scanf("%d", &n);
    int num = fib(n);
    printf("第%d位斐波那契数是%d\n",n, num);
    printf("第三位斐波那契数算了%d次\n", count);
    return 0;
}

 这里第三位斐波那契数算了将近四千万次，所以才会效率这么低。

斐波那契数也是可以用循环来计算的：

#include
int fib(int n)
{
	int result;
	int pre_result;
	int next_older_result;
	result = pre_result = 1;
		while (n > 2)
		{
			n -= 1;
			next_older_result = pre_result;
			pre_result = result;
			result = pre_result + next_older_result;
		}
	return result;
}
int main()

{
	int n = 0;
	scanf("%d", &n);
	int num = fib(n);
	printf("第%d位斐波那契数是%d\n",n, num);
	return 0;
}

 提示：
1. 许多问题是以递归的形式进行解释的，这只是因为它比非递归的形式更为清晰。
2. 但是这些问题的迭代实现往往比递归实现效率更高，虽然代码的可读性稍微差些。
3. 当一个问题相当复杂，难以用迭代实现时，此时递归实现的简洁性便可以补偿它所带来的运行时开销。

四.经典递归案例

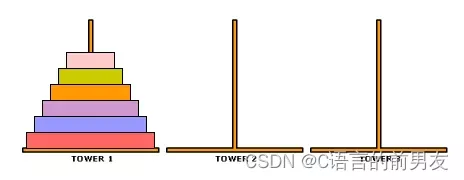
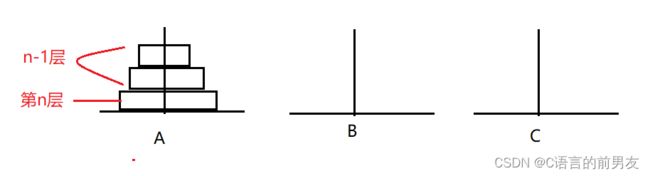
1.汉诺塔

法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说：在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。

 当只有一层时：

 只需要A挪到C就可以了,A—>C;需要 1 步；

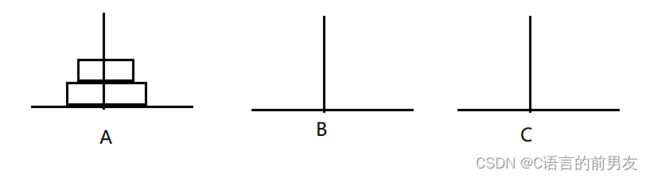
当有两层时：

 需要A—>B，A—>C,B—>C,需要 3 步

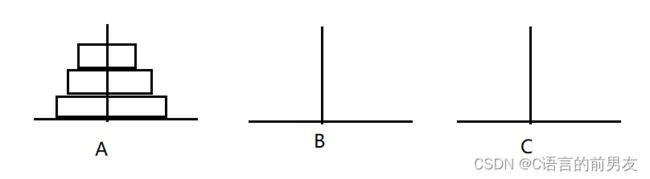
 当有三层时：

A—>B ，A—>C， B—>C， A—>C ，A—>B ，A—>C， B—>C，需要 7 步。

这里就能看出规律：

层数	步数
1	1
2	2^2 -1=3
3	2^3 -1=7
4	2^4-1=15

步数=2的层数的次方减去1,当有n层时，步数：count = 2^n -1;

我们怎么用递归的思路去解决n层的汉诺塔呢？

n我们也可以看成两层，第一层时由n-1层构成的，第二层是第n层。要想完成n层汉诺塔，就必须要先把n-1层放到B上面，再将第n个从A挪到C；最后将n-1层汉诺塔从B挪到C；而把n-1层汉诺塔从A放到B上面，就又是一个n-1层汉诺塔问题了，还是相似的问题，但是规模变小了。所以先把上面n-1层看成一个整体，而n-1层的八个汉诺塔就是递归来完成的，这就是整体去用递归解决问题。

#include
//汉诺塔问题
int Hanoi(int num,char n1,char n2)
{
	static int count = 0;//记录步数；
	if (num == 1)
	{
		printf("%c->%c ", n1, n2);
		count++;
	}
	else
	{
		//将n-1层汉诺塔从A挪到B;
		Hanoi(num - 1,'A','B');
        //将第n个从A挪到C；
		printf("%c->%c ",'A','C');
		count++;
        //将n-1层汉诺塔从B挪到C；
		Hanoi(num - 1, 'B', 'C');
	}
}
int main()
{
	int num = 0;
	printf("请输入汉诺塔层数:>");
	scanf("%d", &num);
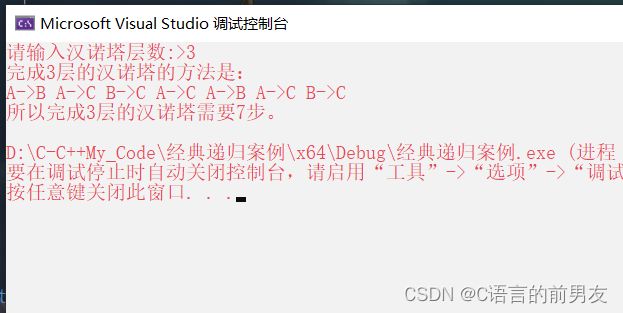
	printf("完成%d层的汉诺塔的方法是：\n", num);
	int sum=Hanoi(num,'A','C');
	printf("\n");
	printf("所以完成%d层的汉诺塔需要%d步。\n",num, sum);
	return 0;
}

 2.青蛙跳台阶

问题描述：一只青蛙一次可以跳上 1 级台阶，也可以跳上2 级。求该青蛙跳上一个n 级的台阶总共有多少种跳法。

一个台阶：有 1 种跳法，跳 一 下。

两个台阶：有 2 种跳法，1 1 或者 2（1代表一次跳一个台阶，2代表一次跳两个台阶，下同）

三个台阶：有 3 种跳法，1 1 1 或者 1 2 或者 2 1；

四个台阶：有 5 种跳法，1 1 1 1，1 2 1，2 1 1，1 1 2 ，2 2；

规律：

台阶数	方法种数
1	1
2	2
3	3
4	5
5	3+5=8
6	5+8=13
n	n-1个台阶跳法 + n-2个台阶跳法

 除了当只有一个台阶和两个台阶时，跳的方法是 1和 2；台阶数大于2以后的方法数都是前两个台阶数的方法数的和。n个台阶数的方法数：count = n-1个台阶跳法 + n-2个台阶跳法。

细心的小伙伴会发现和斐波那契数列很像；

接下来代码就很简单了：

#include
int frog_jump(int num)
{
    //一层台阶
	if (num == 1)
	{
		return 1;
	}
    //两层台阶
	else if (num == 2)
	{
		return 2;
	}
    //大于两层台阶
	else
	{
		return frog_jump(num - 1) + frog_jump(num - 2);
	}
}
int main()
{
	int num = 0;
	printf("请输入台阶数:>");
	scanf("%d", &num);
	int count=frog_jump(num);
	printf("%d层台阶青蛙一共有%d种跳法。\n ",num, count);
    return 0;
}

最后：

       虽然永远无法预料明天是晴还是雨，也无法预知你在乎的人是否还在身旁，以及你一直以来的坚持究竟能否换来什么。但你能决定的是，今天有没有备好雨伞，有没有好好爱自己，以及是否为自己追求的理想而拼尽全力。那些看似不起波澜的日复一日，会在某天让你看到坚持的意义。诸君，山顶见！！！