【动态规划】简单多状态dp问题（2）买卖股票问题

买卖股票问题

【动态规划】简单多状态dp问题（2）买卖股票问题

1. 最佳买卖股票时机含冷冻期（买卖股票Ⅰ）

传送门：力扣309. 最佳买卖股票时机含冷冻期

题目：

1.1 题目解析

越难的dp问题，看示例只能起到了解题目的效果，一般推不出啥普遍的规律，所以接下来就是我们的算法原理，通过动归的思想去理解，才会豁然开朗！

1.2 算法原理

1.2.1 状态表示

我们需要通过经验 + 题目要求去决定状态表示：

1. 根据题目的意境以及数据结构，我们得出需要建立一维的dp表（大小为 n）
   • 对于为什么用一维，首先这道题数据结构为一维的，而一维如果确实可以解决问题就没有必要上升到二维
2. 经验：以某个坐标为结尾或者以某个坐标为起点去研究题目问题！
   • 此题用的是“结尾”

再根据经验，一般dp表的其中一值就应该是答案！

• 所以含义应该就是“最大收益”

综合得到状态表示：dp[i]表示就是从起点到i坐标这些天 结束后 的最大收益

• 应该为结束后，否则会不全面，即第i + 1天干了什么跟dp[i]的值无关，那么最后一天干了什么将没有意义，这是不应该出现的！

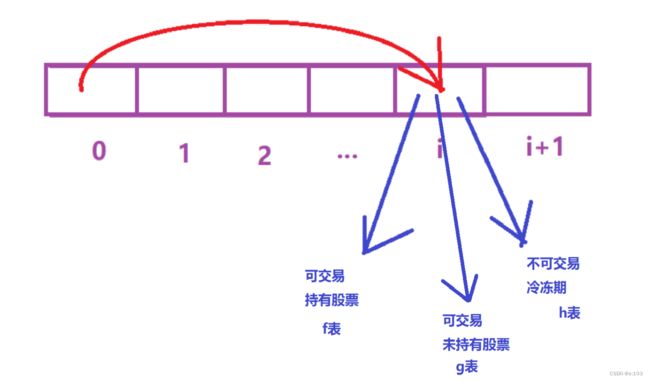
而这道题，与之前做过的题不一样的是，一个坐标的状态有三种情况，需要我们继续细化

1. 持有股票（可交易）
2. 未持有股票（可交易）
3. 冷冻期

所以，最终的状态表示为：

f[i]表示的是，从起点到 i 坐标的这些天结束后，为可交易的持有股票状态的情况下的最大收益

g[i]表示的是，从起点到 i 坐标的这些天结束后，为可交易的未持有股票状态的情况下的最大收益

h[i]表示的是，从起点到 i 坐标的这些天结束后，为不可交易的冷冻期状态的情况下的最大收益

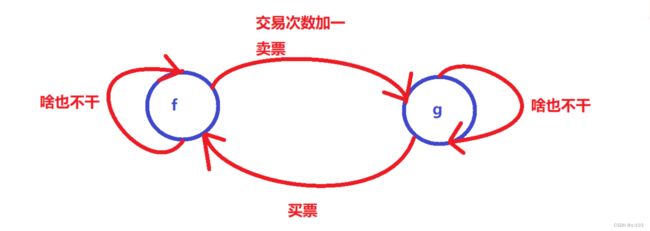
1.2.2 状态机

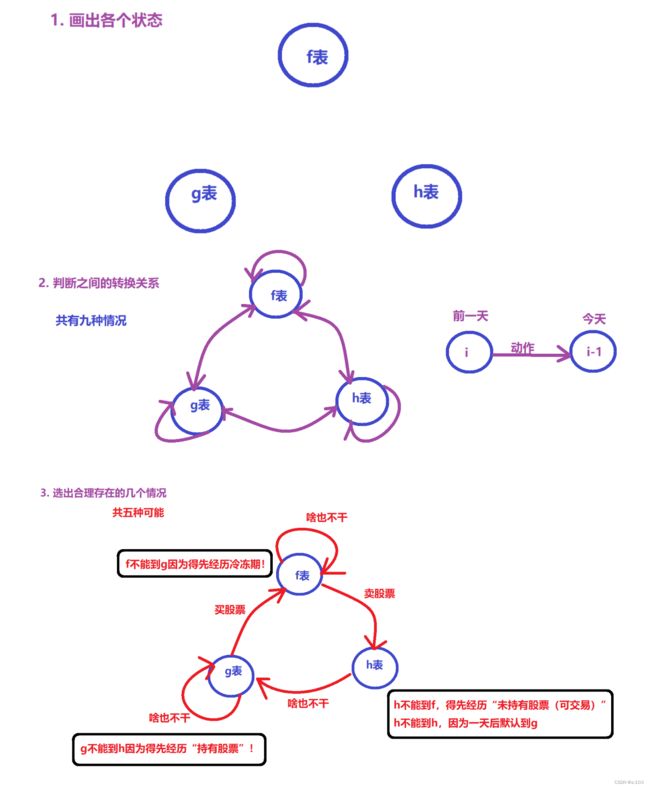
在推导状态转移方程之前，我们要做一些准备工作

• 因为这道题更我们之前做的题不一样，因为从一天到另一天，状态的转换具有一定的逻辑关系，稍微有点复杂并不是“齐次对称的”，而我们需要考虑到各个情况，所以就可以这样做：

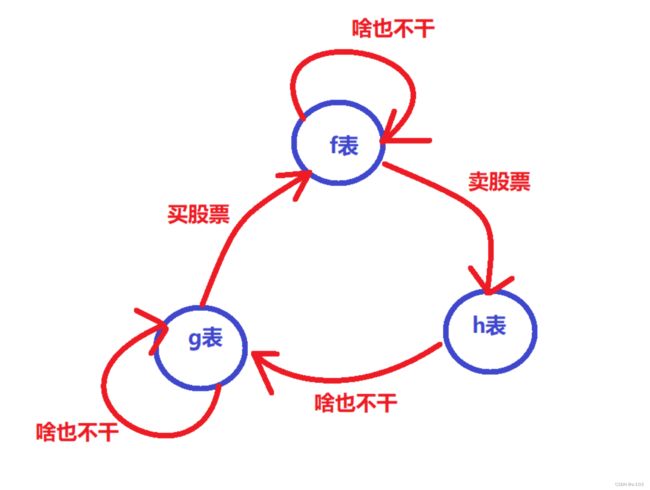
• 所以，最终得出有五种转换关系的存在
  1. 到 f 的有两种
  2. 到 g 的有两种
  3. 到 h 的有一种

而这一幅图，就是”状态机”

1.2.3 状态转移方程

同样的套路，我们需要根据已确定的dp表的值来推导 f[i] 、 g[i] 以及 h[i]的值，并且牢记他们的状态表示！

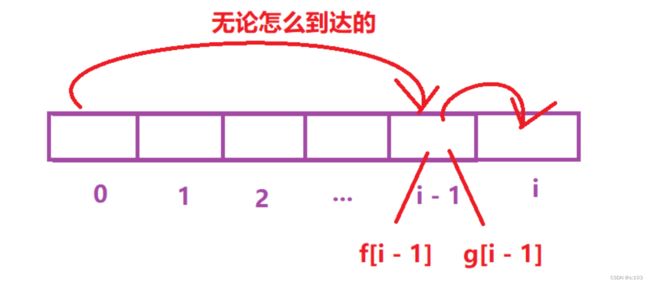
1. 我们以坐标 i 为结尾
2. 根据“最近一步”去划分问题

“最近一步”可以理解为“必然事件”

• 此题的“必然事件”就是，到达坐标 i 之前，必然要先到达坐标 i - 1

结合状态机：

1. 如果这一天结束后为f，那么前一天结束后可能是g或者f

   • 如果前一天是g，则今天的收益应该为g[i - 1] - prices[i]（前一天的收益减去上花掉的钱）
     • 因为g[i - 1]代表第i天结束后为g，则收费应该算的是第i + 1天的费用，即prices[i]
     • 而因此，第i + 1天结束后为f
   • 如果前一天是f，则今天的收益不变，为f[i - 1]
   • 取较大值

2. 如果这一天结束后为g，那么前一天结束后可能为g或者h

   • 如果前一天是g，则今天的收益不变，为g[i - 1]
   • 如果前一天是h，则今天的收益不变，为h[i - 1]
   • 取较大值

3. 如果这一天结束后为h，那么前一天结束后一定为f

   • 今天的收益为f[i - 1] + prices[i] （前一天的收益加上卖掉的钱）
     • 因为f[i - 1]代表第i天结束后为f，则收入应该算的是第i + 1天的费用，即prices[i]
     • 而因此，第i + 1天结束后为h

所以得出状态转移方程：

f[i] = max{g[i - 1] - prices[i], f[i - 1]};

g[i] = max{g[i - 1], h[i - 1]};

h[i] = f[i - 1] + prices[i]

1.2.4 初始化

在第一天结束后

1. 处于f状态，需要买一张票：f[0] = - prices[0]
2. 处于可交易的g状态，啥也不干：g[0] = 0
3. 买一张票立即卖了：h[0] = 0

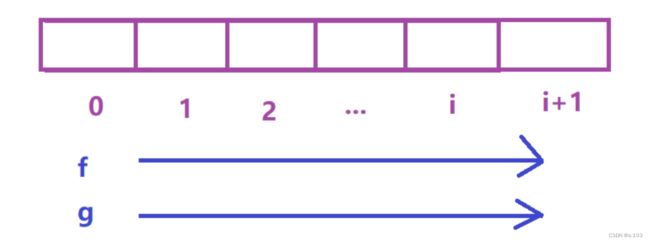
1.2.5 填表顺序

从做到有，三个表一起填

1.2.6 返回值

最后其实处于三种状态都有可能，取较大值即可！

1.3 编写代码

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int[] f = new int[n];
        int[] g = new int[n];
        int[] h = new int[n];
        f[0] = -prices[0];
        for(int i = 1; i < n; i++) {
            f[i] = Math.max(f[i - 1], g[i - 1] - prices[i]);
            g[i] = Math.max(g[i - 1], h[i - 1]);
            h[i] = f[i - 1] + prices[i];
        }
        return Math.max(
            Math.max(f[n - 1], g[n - 1]), h[n - 1]
        );
    }
}

时空复杂度都为：O(N)

2. 买卖股票的最佳时机含手续费（买卖股票Ⅱ）

传送门：力扣714. 买卖股票的最佳时机含手续费

题目：

2.1 题目解析

越难的dp问题，看示例只能起到了解题目的效果，一般推不出啥普遍的规律，所以接下来就是我们的算法原理，通过动归的思想去理解，才会豁然开朗！

2.2 算法原理

2.2.1 状态表示

我们需要通过经验 + 题目要求去决定状态表示：

1. 根据题目的意境以及数据结构，我们得出需要建立一维的dp表（大小为 n）
   • 对于为什么用一维，首先这道题数据结构为一维的，而一维如果确实可以解决问题就没有必要上升到二维
2. 经验：以某个坐标为结尾或者以某个坐标为起点去研究题目问题！
   • 此题用的是“结尾”

再根据经验，一般dp表的其中一值就应该是答案！

• 所以含义应该就是“最长预约时长”

综合得到状态表示：dp[i]表示就是起点到坐标为 i 的位置【这些天结束后】的最大收益

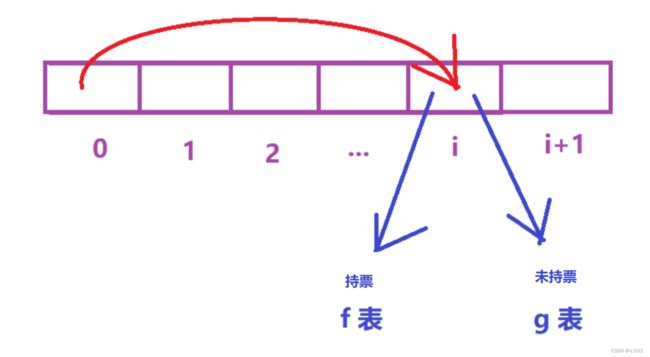
而这道题，与之前做过的题不一样的是，一个坐标的状态有两种情况，需要我们继续细化

1. 持票
2. 未持票

所以，最终的状态表示为：

f[i]表示的是，从起点到 i 坐标的这些天结束后，持票的情况下的最大收益

g[i]表示的是，从起点到 i 坐标的这些天结束后，未持票的情况下的最大收益

2.2.3 状态机

同样的画一下状态机：

2.2.3 状态转移方程

同样的套路，我们需要根据已确定的dp表的值来推导 f[i] 和 g[i] 的值，并且牢记他们的状态表示！

1. 我们以坐标 i 为结尾
2. 根据“最近一步”去划分问题

“最近一步”可以理解为“必然事件”

• 此题的“必然事件”就是，到达坐标 i 之前，必然要先到达坐标 i - 1
  

1. 这一天结束后为持票的话，前一天结束后可能为f或者g
   • f的话，收益不变，为f[i - 1]
   • g的话，支付票价，为g[i - 1] - prices[i]
2. 这一天结束后为未持票的话，前一天结束后可能为f或者g
   • f的话，支付手续费获得收入，为f[i - 1] + prices[i] - fee
   • g的话，收益不变，为g[i - 1]

而1代表着f表怎么填，2代表着g表怎么填

所以得出状态转移方程：

f[i] = max{f[i - 1], g[i - 1] - prices[i]};

g[i] = max{f[i - 1] + prices[i] - fee, g[i - 1]};

2.2.4 初始化

在第一天结束后

1. 为持票状态，即买一张票，为prices[0] * (-1)
2. 为未持票状态，啥也不干，为0

2.2.5 填表顺序

从左往右两个表一起填

2.2.6 返回值

最后一天结束后，两种情况收益的较大值

2.3 编写代码

class Solution {
    public int maxProfit(int[] prices, int fee) {
        int n = prices.length;
        int[] f = new int[n];
        int[] g = new int[n];
        f[0] = -prices[0];
        for(int i = 1; i < n; i++) {
            f[i] = Math.max(f[i - 1], g[i - 1] - prices[i]);
            g[i] = Math.max(g[i - 1], f[i - 1] + prices[i] - fee);
        }
        return Math.max(f[n - 1], g[n - 1]);
    }
}

时空复杂度都为：O(N)

3. 买卖股票的最佳时期限制次数（买卖股票Ⅲ）

传送门：力扣123.买卖股票的最佳时机 III

题目：

3.1 题目解析

越难的dp问题，看示例只能起到了解题目的效果，一般推不出啥普遍的规律，所以接下来就是我们的算法原理，通过动归的思想去理解，才会豁然开朗！

3.2 算法原理

3.2.1 状态表示

我们需要通过经验 + 题目要求去决定状态表示：

1. 根据题目的意境以及数据结构，我们得出需要建立二维的dp表（大小为 n × 3）
2. 经验：以某个坐标为结尾或者以某个坐标为起点去研究题目问题！
   • 此题用的是“结尾”

再根据经验，一般dp表的其中一值就应该是答案！

• 所以含义应该就是“最大收益”

综合得到状态表示：dp[i][j]表示就是起点到坐标为 i 的位置这些天结束后交易次数为j的最大收益

而这道题，与之前做过的题不一样的是，一个坐标的状态有两种情况，需要我们继续细化

1. 持票
2. 未持票

在之前的题目里，我们到达一个坐标并无其他选择，而现在有~

所以，最终的状态表示为：

f[i] [j]表示的是，从起点到 i 坐标的这些天结束后，持票且交易次数为 j 的情况下的最大收益

g[i] [j]表示的是，从起点到 i 坐标的这些天结束，未持票且交易次数为 j 的情况下的最大收益

3.2.2 状态机

3.2.3 状态转移方程

同样的套路，我们需要根据已确定的dp表的值来推导 f[i] [j] 和 g[i] [j]的值，并且牢记他们的状态表示！

1. 我们以坐标 i 为结尾
2. 根据“最近一步”去划分问题

“最近一步”可以理解为“必然事件”

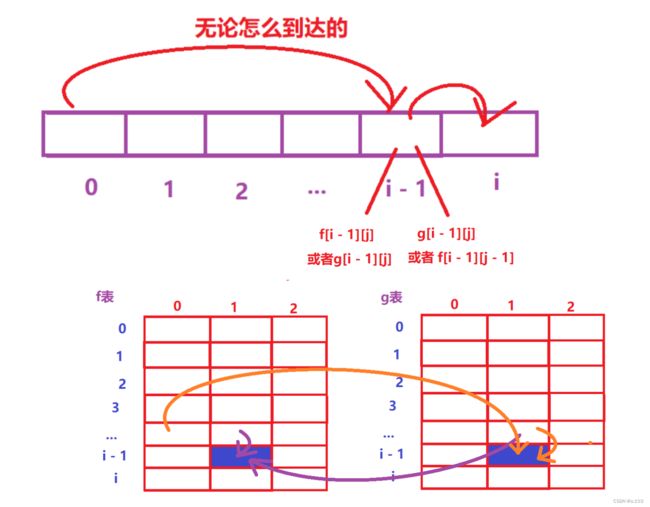
• 此题的“必然事件”就是走到(i, j)之前，
  1. f表，先要走到(i - 1, j)
  2. g表，先要走到(i - 1, j - 1)或者(i - 1, j)
     • 完成第j次交易之前，要先完成第j-1次交易

1. 这一天结束后为持票的话，前一天结束后可能为f或者g
   • f的话，收益不变，为f[i - 1] [j]
   • g的话，支付票价，为g[i - 1] [j] - prices[i]
2. 这一天结束后为未持票的话，前一天结束后可能为f或者g
   • f的话，支付手续费获得收入，为f[i - 1] [j - 1] + prices[i]
   • g的话，收益不变，为g[i - 1] [j]

而1代表着f表怎么填，2代表着g表怎么填

所以得出状态转移方程：

f[i] [j] = max{f[i - 1] [j], g[i - 1] [j] - prices[i]};

g[i] [j] = max{g[i - 1] [j], f[i - 1] [j - 1] + prices[i]};

问题：怎么做到限制次数的？

首先，到达交易三次的前提是到达交易两次

• 那么，交易两次后，其值并没有追加在其他元素上，那么就不会增加交易次数

依此限制了交易次数

3.2.4 初始化

初始化：

f表：

• 第0行：f[0] [0] = - prices[0] 、f[0] [1] = -∞、f[0] [2] = -∞（取-∞这是因为不存在这种可能）
  • -∞取MIN_VALUE的话，由于上面设计一个减操作，所以它反而变成了一个很大的正数，而我们想要的是让其绝对不会被选中，所以应该让 -∞ = -0x3f3f3f3f（常用的无穷大数）

g表：

• 第0行：g[0] [0] = 0 、g[0] [1] = -∞、g[0] [2] = -∞（取-∞这是因为不存在这种可能）
• 第0列：都为0（其实g[i] [0] = g[i - 1] [0]，可以在状态转移方程中去处理）

即，g表的状态转移方程为：

1. g[i] [j] = g[i - 1] [j]
2. 如果j >= 1，g[i] [j] = max{g[i] [j], f[i - 1] [j - 1]};

3.2.5 填表顺序

从上到下两个表一起填每一行，每一行每一列一起填

3.2.6 返回值

最后一天结束后，f或者g状态下，各个交易次数都要算上，去最大值！

3.3 编写代码

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int[][] f = new int[n][3];
        int[][] g = new int[n][3];

        f[0][0] = -prices[0];
        for(int i = 1; i < 3; i++) {
            f[0][i] = -0x3f3f3f3f;
            g[0][i] = -0x3f3f3f3f;
        }
        for(int i = 1; i < n; i++) {
            for(int j = 0; j < 3; j++) {
                f[i][j] = Math.max(f[i - 1][j], g[i - 1][j] - prices[i]);
                g[i][j] = g[i - 1][j];
                if(j >= 1) {
                    g[i][j] = Math.max(g[i][j], f[i - 1][j - 1] + prices[i]);
                }
            }
        }
        int min = -0x3f3f3f3f;
        for(int i = 0; i < 3; i++) {
            min = Math.max(min, f[n - 1][i]);
            min = Math.max(min, g[n - 1][i]);
        }
        return min;
    }
}

时空复杂度都为：O(N)

4. 买卖股票的最佳实际限制次数（买卖股票Ⅳ）

传送门：力扣188. 买卖股票的最佳时机 IV

题目：

4.1 与第三题的关系

这道题，跟第三题唯一的区别就是，第三题限制为2次，而这道题限制为k次

• 而2次只不过是k次中的其中一种情况罢了，而他们的解法，一模一样！

第三题的dp表是n × 3，填表时因为空间的限制，无法达到3次及以上

那么这道题，dp表设为n × (k + 1)，填表由于空间限制，也无法达到k次以上

• 由于影响值的只有左上或者上侧，所以右侧的列的存在并不会影响左侧的值
• 也就是说，如果这个很大的表是通用的，使用其的一部分，就能解决个别的问题

4.2 编写代码

class Solution {
    public int maxProfit(int k, int[] prices) {
        int n = prices.length;
        int[][] f = new int[n][k + 1];
        int[][] g = new int[n][k + 1];

        f[0][0] = -prices[0];
        for(int i = 1; i < k + 1; i++) {
            f[0][i] = -0x3f3f3f3f;
            g[0][i] = -0x3f3f3f3f;
        }
        for(int i = 1; i < n; i++) {
            for(int j = 0; j < k + 1; j++) {
                f[i][j] = Math.max(f[i - 1][j], g[i - 1][j] - prices[i]);
                g[i][j] = g[i - 1][j];
                if(j >= 1) {
                    g[i][j] = Math.max(g[i][j], f[i - 1][j - 1] + prices[i]);
                }
            }
        }
        int min = -0x3f3f3f3f;
        for(int i = 0; i < k + 1; i++) {
            min = Math.max(min, f[n - 1][i]);
            min = Math.max(min, g[n - 1][i]);
        }
        return min;
    }
}

时空复杂度都为：O(N * k)

---

文章到此结束！谢谢观看
可以叫我 小马，我可能写的不好或者有错误，但是一起加油鸭！

本文代码链接：动态规划04/src/Main.java · 游离态/马拉圈2023年6月 - 码云 - 开源中国 (gitee.com)

---