Leetcode之二分查找
1. 二分查找
二分查找的前提条件是:有序数组。
二分查找的递归实现:
class Solution:
def search_recur(self,nums:List[int],low:int,high:int,target:int):
if low > high:return -1
mid = low + (high - low) // 2
if nums[mid] == target:
return mid
elif nums[mid] > target:
return self.search_recur(nums,low,mid-1,target)
else:
return self.search_recur(nums,mid+1,high,target)
def search(self, nums: List[int], target: int) -> int:
n = len(nums)
low = 0
high = n - 1
return self.search_recur(nums,low,high,target)
二分查找的迭代实现:
class Solution:
def search(self, nums: List[int], target: int) -> int:
n = len(nums)
low = 0
high = n - 1
while(low<=high):
mid = low + (high-low)//2
if nums[mid] == target:
return mid
if nums[mid] > target:
high = mid - 1
elif nums[mid] < target:
low = mid + 1
return -1
2. 二分查找的变形
2.1. 查找第一个大于等于目标值的下标
- 向前看一眼
对于这种情况,当我们通过二分查找,找到第一个大于等于target的元素的时候,需要看一下mid左边的值是否也大于等于target,如果是,则我们需要继续对[low,mid-1]进行二分查找,如果不是,则说明mid就是我们要找的元素。
class Solution:
def search(self, nums: List[int], target: int) -> int:
n = len(nums)
low = 0
high = n - 1
while(low<=high):
mid = low + (high-low)//2
if nums[mid] >= target:
if mid == 0 or nums[mid-1] < target:
return mid
else:
high = mid - 1
elif nums[mid] < target:
low = mid + 1
return -1
2.2. 查找最后一个等于目标值的下标
- 向后看一眼
对于这种情况,当我们通过二分查找,找到第一个等于target的元素的时候,需要看一下mid右边的值是否也等于target,如果是,则我们需要继续对[mid+1,high]进行二分查找,如果不是,则说明mid就是我们要找的元素。
class Solution:
def search(self, nums: List[int], target: int) -> int:
n = len(nums)
low = 0
high = n - 1
while(low<=high):
mid = low + (high-low)//2
if nums[mid] == target:
if mid == n-1 or nums[mid+1] != target:
return mid
else:
low = mid + 1
elif nums[mid] < target:
low = mid + 1
elif nums[mid] > target:
high = mid - 1
return -1
3. 相关算法题
3.1. Leetcode 34 在排序数组中查找元素的第一个和最后一个位置
-
题目链接
-
解题思路
参考上面的二分查找的变形,我们可以分别找到第一个大于等于target的下标和最后一个等于target的下标,然后返回这两个下标即可。
class Solution:
def searchFirst(self, nums: List[int], target: List[int]) -> int:
n = len(nums)
low = 0
high = n - 1
while low <= high:
mid = low + (high - low) // 2
if nums[mid] == target:
if mid == 0 or nums[mid-1] != target:
return mid
else:
high = mid - 1
else:
if nums[mid] > target:
high = mid - 1
else:
low = mid + 1
return -1
def searchLast(self,nums:List[int],target:List[int])->int:
n = len(nums)
low = 0
high = n - 1
while low <= high:
mid = low + (high - low) // 2
if nums[mid] == target:
if mid == n - 1 or nums[mid+1] != target:
return mid
else:
low = mid + 1
else:
if nums[mid] > target:
high = mid - 1
else:
low = mid + 1
return -1
def searchRange(self, nums: List[int], target: int) -> List[int]:
return [self.searchFirst(nums,target),self.searchLast(nums,target)]
3.2. Leetcode 35 搜索插入位置
- 题目链接
- 解题思路:参考上面的二分查找的变形,我们可以找到第一个大于等于target的下标,然后返回这个下标即可。
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
# 这相当于找到第一个大于等于target值的元素索引
n = len(nums)
low = 0
high = n - 1
while(low <= high):
mid = low + (high - low) // 2
if nums[mid] >= target:
if mid == 0 or nums[mid-1] < target:
return mid
else:
high = mid - 1
else:
low = mid + 1
# 说明此时没有任何一个元素大于等于target,则它应放在最后一个元素
return n
第二种解法。另一种方法是
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
# 这相当于找到第一个大于等于target值的元素索引
n = len(nums)
low = 0
high = n # 注意此处,不是n-1,而是n,因为插入位置有可能是最后一个元素的后面
while(low<high):
"""
查找第一个大于等于target的元素的下标,如果在数组里面找不到,则返回数组长度。
"""
mid = low + (high-low) // 2
if nums[mid] >= target:
high = mid
else:
low = mid + 1
return low
以上代码的核心是查找了第一个大于等于target的元素的下标,如果在数组里面找不到,则返回数组的最后一个元素的下标+1,即为数组的长度。
需要注意的是,这里的high = n,而不是n-1,因为插入位置有可能是最后一个元素的后面。
3.3. Leetcode 278 第一个错误的版本
- 题目链接
- 解题思路
这道题目其实就是找到第一个大于等于target的元素的下标,然后返回这个下标即可。
以下是原始思路
class Solution:
def firstBadVersion(self, n: int) -> int:
versions = [i for i in range(1,n+1)]
low = 0
length = len(versions)
high = n - 1
while(low <= high):
mid = low + (high-low) // 2
if isBadVersion(versions[mid]):
if mid == 0 or not isBadVersion(versions[mid-1]):
return versions[mid]
else:
high = mid - 1
else:
low = mid + 1
return versions[-1]
但是这种思路会超出内存限制,所以将versions取出,versions[i] = i + 1,最后的代码为:
class Solution:
def firstBadVersion(self, n: int) -> int:
low = 0
high = n - 1
while(low <= high):
mid = low + (high-low) // 2
if isBadVersion(mid+1):
if mid == 0 or not isBadVersion(mid):
return mid+1
else:
high = mid - 1
else:
low = mid + 1
return n
3.4. Plus 旋转数组
- 什么是旋转数组
旋转数组是指将一个数组的前面若干个元素搬到数组的后面,从而形成一个新的数组。它的特点是前面的元素是有序的,后面的元素也是有序的,但是整体的数组是无序的。
比如:[4,5,6,7,1,2,3]是[1,2,3,4,5,6,7]的一个旋转数组,前者是后者在下标k=3处旋转得到的。
- 给定一个旋转数组和mid值,如何判断左边有序还是右边有序?
我们可以通过比较nums[mid]和nums[low]的大小来判断左边有序还是右边有序,如果nums[mid] >= nums[low],则说明左边有序,否则右边有序。
例如:[4,5,6,7,1,2,3],mid = 3,low = 0,high = 6,nums[mid] = 7,nums[low] = 4,nums[mid] > nums[low],则说明左边有序,右边无序。
3.5. Leetcoee 33 搜索旋转数组
- 题目描述
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
提示:
1 <= nums.length <= 5000
-104 <= nums[i] <= 104
nums 中的每个值都 独一无二
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-104 <= target <= 104
-
题目链接
-
解题思路
参考上面的分析,我们可以通过比较nums[mid]和nums[low]的大小来判断左边有序还是右边有序,然后根据target和nums[mid]的大小关系来判断target在左边还是右边,然后对左边或者右边进行二分查找即可。
class Solution:
def search(self, nums: List[int], target: int) -> int:
low = 0
n = len(nums)
high = n - 1
while(low<=high):
mid = low + (high-low)//2
if nums[mid] == target:
return mid
if nums[low] <= nums[mid]: # 左侧有序
if nums[low] <= target < nums[mid]:
high = mid - 1
else:
low = mid + 1
else: # 右侧有序
if nums[mid] < target <= nums[high]:
low = mid + 1
else:
high = mid - 1
return -1
3.6. Leetcode 153 寻找旋转排序数组中的最小值
- 题目描述
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。
示例 3:
输入:nums = [11,13,15,17]
输出:11
解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
提示:
n == nums.length
1 <= n <= 5000
-5000 <= nums[i] <= 5000
nums 中的所有整数 互不相同
nums 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
-
题目链接
-
解题思路
参考上面的分析,我们可以通过比较nums[mid]和nums[low]的大小来判断左边有序还是右边有序,然后对左边或者右边进行二分查找,查找停止的条件是到最后一个值或者nums[mid] > nums[mid+1],然后返回min(nums[0],nums[mid+1])即可。
class Solution:
def findMin(self, nums: List[int]) -> int:
"""
1 4 6 8 9
9 1 4 6 8
8 9 1 4 6
"""
low = 0
n = len(nums)
high = n - 1
k = -1
while(low<=high):
mid = low + (high - low) // 2
if mid == n - 1 or nums[mid] > nums[mid+1]:
k = mid + 1 if (mid + 1) < (n-1) else n-1
break
else:
if nums[low] <= nums[mid]: # 左侧有序
low = mid + 1
else:
high = mid - 1
return min(nums[0],nums[k])
其实,对于旋转数组中,最小值的搜索,有一种通用解法。
判断nums[mid]和nums[high]之间的关系,如果nums[mid] > nums[high],说明最小值在右侧,否则在左侧(这里的左侧包括mid)。
比如,我们有以下两种情况:
5 6 7 8 9 1 2 3 4
因为数组旋转的过程中,一定是先从最大值放到前面开始,然后再将次大值放到前面,以此类推,所以nums[mid] > nums[high],说明最小值在右侧,否则在左侧(这里的左侧包括mid)。
class Solution:
def findMin(self, nums: List[int]) -> int:
low = 0
n = len(nums)
high = n - 1
k = -1
while(low<high):
mid = low + (high - low) // 2
if nums[mid] < nums[high]: # 右侧有序
high = mid
else:
low = mid + 1
return nums[low]
3.7. Leetcode 154 寻找旋转排序数组中的最小值 II
- 题目描述
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到:
若旋转 4 次,则可以得到 [4,5,6,7,0,1,4]
若旋转 7 次,则可以得到 [0,1,4,4,5,6,7]
注意,数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个可能存在 重复 元素值的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须尽可能减少整个过程的操作步骤。
示例 1:
输入:nums = [1,3,5]
输出:1
示例 2:
输入:nums = [2,2,2,0,1]
输出:0
提示:
n == nums.length
1 <= n <= 5000
-5000 <= nums[i] <= 5000
nums 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
进阶:这道题与 寻找旋转排序数组中的最小值 类似,但 nums 可能包含重复元素。允许重复会影响算法的时间复杂度吗?会如何影响,为什么?
-
题目链接 https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array-ii/
-
解题思路
需要注意的是,如果还是按照1中的思路,有可能会错过最小值,如下面的例子:
[10,1,10,10,10],所以需要对nums[mid] == nums[high]的情况进行特殊处理,high -= 1即可。
class Solution:
def findMin(self, nums: List[int]) -> int:
low = 0
n = len(nums)
if n == 0:return nums[0]
high = n - 1
k = -1
while (low < high):
mid = low + (high - low ) // 2
if nums[mid] == nums[high]:
high -= 1
elif nums[mid] > nums[high]:
low = mid + 1
else:
high = mid
return nums[low]
3.8. 剑指 Offer II 069 山峰数组的顶部
- 题目描述
符合下列属性的数组 arr 称为 山峰数组(山脉数组) :
arr.length >= 3
存在 i(0 < i < arr.length - 1)使得:
arr[0] < arr[1] < ... arr[i-1] < arr[i]
arr[i] > arr[i+1] > ... > arr[arr.length - 1]
给定由整数组成的山峰数组 arr ,返回任何满足 arr[0] < arr[1] < … arr[i - 1] < arr[i] > arr[i + 1] > … > arr[arr.length - 1] 的下标 i ,即山峰顶部。
示例 1:
输入:arr = [0,1,0]
输出:1
示例 2:
输入:arr = [1,3,5,4,2]
输出:2
示例 3:
输入:arr = [0,10,5,2]
输出:1
示例 4:
输入:arr = [3,4,5,1]
输出:2
示例 5:
输入:arr = [24,69,100,99,79,78,67,36,26,19]
输出:2
提示:
3 <= arr.length <= 104
0 <= arr[i] <= 106
题目数据保证 arr 是一个山脉数组
进阶:很容易想到时间复杂度 O(n) 的解决方案,你可以设计一个 O(log(n)) 的解决方案吗?
-
题目链接
-
解题思路
这道题目其实就是找到最大值所在的下标,所以我们可以通过二分查找的方式来找到最大值所在的下标。而且,因为题目中说了,题目数据保证 arr 是一个山脉数组,所以我们可以不用考虑边界条件,直接返回最大值所在的下标即可。即,终止条件为nums[mid-1] < nums[mid] > nums[mid+1],返回mid。
from cn.Python3.mod.preImport import *
class Solution:
def peakIndexInMountainArray(self, arr: List[int]) -> int:
# 相当于找到最大值所在的下标
low = 0
n = len(arr)
high = n - 1
while(low<high):
mid = low + (high-low) // 2
if mid != 0 and mid != n-1 and arr[mid-1] < arr[mid] > arr[mid+1]:
return mid
elif mid !=0 and mid!= n-1 and arr[mid-1] < arr[mid] < arr[mid+1]:
low = mid
else:
high = mid
return -1
3.9. Leetcode 1095 山脉数组中查找目标值
- 题目描述
(这是一个 交互式问题 )
给你一个 山脉数组 mountainArr,请你返回能够使得 mountainArr.get(index) 等于 target 最小 的下标 index 值。
如果不存在这样的下标 index,就请返回 -1。
何为山脉数组?如果数组 A 是一个山脉数组的话,那它满足如下条件:
首先,A.length >= 3
其次,在 0 < i < A.length - 1 条件下,存在 i 使得:
A[0] < A[1] < ... A[i-1] < A[i]
A[i] > A[i+1] > ... > A[A.length - 1]
你将 不能直接访问该山脉数组,必须通过 MountainArray 接口来获取数据:
MountainArray.get(k) - 会返回数组中索引为k 的元素(下标从 0 开始)
MountainArray.length() - 会返回该数组的长度
注意:
对 MountainArray.get 发起超过 100 次调用的提交将被视为错误答案。此外,任何试图规避判题系统的解决方案都将会导致比赛资格被取消。
为了帮助大家更好地理解交互式问题,我们准备了一个样例 “答案”:https://leetcode-cn.com/playground/RKhe3ave,请注意这 不是一个正确答案。
示例 1:
输入:array = [1,2,3,4,5,3,1], target = 3
输出:2
解释:3 在数组中出现了两次,下标分别为 2 和 5,我们返回最小的下标 2。
示例 2:
输入:array = [0,1,2,4,2,1], target = 3
输出:-1
解释:3 在数组中没有出现,返回 -1。
提示:
3 <= mountain_arr.length() <= 10000
0 <= target <= 10^9
0 <= mountain_arr.get(index) <= 10^9
-
题目链接
-
解题思路
这道题目其实就是找到最大值所在的下标,然后在左侧和右侧分别进行二分查找即可。其实这是因为测试用例放水了,如果严格按照不大于100次,其实测试用例搞一个极限条件,应该是会超过100次的。
# """
# This is MountainArray's API interface.
# You should not implement it, or speculate about its implementation
# """
#class MountainArray:
# def get(self, index: int) -> int:
# def length(self) -> int:
class Solution:
def find_peak_index(self,mountain_arr) -> int:
n = mountain_arr.length()
low = 0
high = n - 1
while(low<=high):
mid = low + (high-low) // 2
mid_val = mountain_arr.get(mid)
if mid != 0 and mid != n-1:
last_val = mountain_arr.get(mid - 1)
next_val = mountain_arr.get(mid + 1)
if last_val < mid_val > next_val:
return mid,mid_val
elif last_val < mid_val < next_val:
low = mid + 1
else:
high = mid - 1
return -1,None
def binarySearchFront(self,target:int,mountain_arr,low:int,high:int):
if low > high:
return -1
mid = low + (high-low) // 2
mid_val = mountain_arr.get(mid)
if mid_val == target:
return mid
elif mid_val > target:
return self.binarySearchFront(target,mountain_arr,low,mid-1)
else:
return self.binarySearchFront(target,mountain_arr,mid+1,high)
def binarySearchLatter(self,target:int,mountain_arr,low:int,high:int):
if low > high:
return -1
mid = low + (high-low) // 2
mid_val = mountain_arr.get(mid)
if mid_val == target:
return mid
elif mid_val < target:
return self.binarySearchLatter(target,mountain_arr,low,mid-1)
else:
return self.binarySearchLatter(target,mountain_arr,mid+1,high)
def findInMountainArray(self, target: int, mountain_arr: 'MountainArray') -> int:
mountain_arr = mountain_arr
n = mountain_arr.length()
low = 0
high = n - 1
peak_index,peak_val = self.find_peak_index(mountain_arr)
index = self.binarySearchFront(target,mountain_arr,low,peak_index+1)
if index != -1:return index
return self.binarySearchLatter(target,mountain_arr,peak_index,high)
3.10 Leetcode 162 寻找峰值
- 题目描述
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
提示:
1 <= nums.length <= 1000
-231 <= nums[i] <= 231 - 1
对于所有有效的 i 都有 nums[i] != nums[i + 1]
- 题目链接
- 思路分析
这是一种单独的情况,对于没有相同元素的数组,首先确定nums[mid]和nums[mid+1]不可能相等,如果nums[mid] > nums[mid+1],则说明峰值在左侧,如果nums[mid] < nums[mid+1],则说明峰值在右侧,然后对左侧或者右侧进行二分查找即可。其中,左侧包括mid,右侧不包括mid。
举例:(其中l=low,m=mid,h=high)
4 2 1 3 7 6 5
l m h
4 2 1 3 7 6 5
l m h
4 2 1 3 7 6 5
lm h
4 2 1 3 7 6 5
lhm
return low
class Solution:
def findPeakElement(self, nums: List[int]) -> int:
low = 0
n = len(nums)
high = len(nums) - 1
while(low < high):
mid = low + (high - low) // 2
if nums[mid] < nums[mid+1]:
low = mid + 1
elif nums[mid] > nums[mid+1]:
high = mid
return low
3.11 Leetcode 240 搜索二维矩阵 II
- 题目描述
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
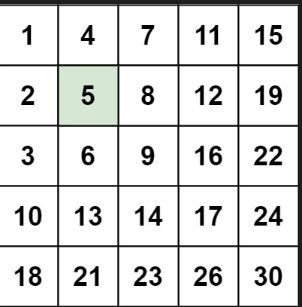
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
- 提示
m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-109 <= matrix[i][j] <= 109
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-109 <= target <= 10
-
题目链接
-
解题思路
沿着对角线元素遍历,设当前元素为(i,i),则矩阵中[matrix[i][p] for p in range(i,n)]和[matrix[p][i] for p in range(i,m)]都是有序的,所以我们可以对这两个数组进行二分查找,如果找到了,则返回True,否则返回False。
class Solution:
def recur_search(self,nums:List[int],low:int,high:int,target:int):
if low > high:
return -1
mid = low + (high-low) // 2
if target == nums[mid]:
return mid
if target > nums[mid]:
return self.recur_search(nums,mid+1,high,target)
elif target < nums[mid]:
return self.recur_search(nums,low,mid-1,target)
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
m = len(matrix)
n = len(matrix[0])
k = min(m,n)
i = 0
while(i<k):
nums = [matrix[i][p] for p in range(i,n)]
if self.recur_search(nums,0,len(nums)-1,target) != -1:
return True
nums = [matrix[p][i] for p in range(i,m)]
if self.recur_search(nums,0,len(nums)-1,target) != -1:
return True
i += 1
return False
3.12 Leetcode 1539 第 k 个缺失的正整数
- 题目描述
第 k 个缺失的正整数
给你一个 严格升序排列 的正整数数组 arr 和一个整数 k 。
请你找到这个数组里第 k 个缺失的正整数。
示例 1:
输入:arr = [2,3,4,7,11], k = 5
输出:9
解释:缺失的正整数包括 [1,5,6,8,9,10,12,13,...] 。第 5 个缺失的正整数为 9 。
示例 2:
输入:arr = [1,2,3,4], k = 2
输出:6
解释:缺失的正整数包括 [5,6,7,...] 。第 2 个缺失的正整数为 6 。
提示:
1 <= arr.length <= 1000
1 <= arr[i] <= 1000
1 <= k <= 1000
对于所有 1 <= i < j <= arr.length 的 i 和 j 满足 arr[i] < arr[j]
进阶:
你可以设计一个时间复杂度小于 O(n) 的算法解决此问题吗?
-
题目链接
-
思路分析
对于arr中的任意一个数字,其前面缺失的正整数数字个数为arr[i] - i - 1,所以我们可以通过二分查找的方式来找到第k个缺失的数字。
class Solution:
def __init__(self) -> None:
self.arr = None
def get_mis_num(self,i:int):
return self.arr[i] - i - 1
def findKthPositive(self, arr: List[int], k: int) -> int:
self.arr = arr
if self.get_mis_num(0) > k : return k
low,high = 0,len(arr)
while(low<high):
mid = low + (high-low) // 2
if self.get_mis_num(mid) >=k:
high = mid
else:
low = mid + 1
return arr[low-1] + k-self.get_mis_num(low-1)