《异常检测——从经典算法到深度学习》21 Anomaly Transformer：具有关联差异的时间序列异常检测

《异常检测——从经典算法到深度学习》

• 0 概论
• 1 基于隔离森林的异常检测算法
• 2 基于LOF的异常检测算法
• 3 基于One-Class SVM的异常检测算法
• 4 基于高斯概率密度异常检测算法
• 5 Opprentice——异常检测经典算法最终篇
• 6 基于重构概率的 VAE 异常检测
• 7 基于条件VAE异常检测
• 8 Donut: 基于 VAE 的 Web 应用周期性 KPI 无监督异常检测
• 9 异常检测资料汇总（持续更新&抛砖引玉）
• 10 Bagel: 基于条件 VAE 的鲁棒无监督KPI异常检测
• 11 ADS: 针对大量出现的KPI流快速部署异常检测模型
• 12 Buzz: 对复杂 KPI 基于VAE对抗训练的非监督异常检测
• 13 MAD: 基于GANs的时间序列数据多元异常检测
• 14 对于流数据基于 RRCF 的异常检测
• 15 通过无监督和主动学习进行实用的白盒异常检测
• 16 基于VAE和LOF的无监督KPI异常检测算法
• 17 基于 VAE-LSTM 混合模型的时间异常检测
• 18 USAD：多元时间序列的无监督异常检测
• 19 OmniAnomaly：基于随机循环网络的多元时间序列鲁棒异常检测
• 20 HotSpot：多维特征 Additive KPI 的异常定位
• 21 Anomaly Transformer: 基于关联差异的时间序列异常检测)

相关：

• VAE 模型基本原理简单介绍
• GAN 数学原理简单介绍以及代码实践
• 单指标时间序列异常检测——基于重构概率的变分自编码（VAE）代码实现（详细解释）

21. Anomaly Transformer：具有关联差异的时间序列异常检测

论文名称：ANOMALY TRANSFORMER: TIME SERIES ANOMALY DETECTION WITH ASSOCIATION DISCREPANCY
论文发表于 ICLR
论文下载：arxiv
源码地址：https://github.com/thuml/Anomaly-Transformer
论文理解需要对 transformer 有一定的了解，推荐初学者速读 史上最小白之Transformer详解 | Transformer 模型详解

21.1 论文概述

这里首先介绍一下论文中每个章节的大体内容：

这里特地说明一下，小伙伴们不要过于在意算法的结果，重点应当放在算法原理以及借鉴意义方面。不同的人研究对象、研究方向往往是不同的，所以无论是哪一种算法都会有它的适用性和缺陷，常常有小伙伴私信我为什么自己跑出来的效果比较差，完全没有论文提到的……特地在这里强调梳理论文的重点应当在于梳理结构与原理，思考如何参考这个思路，这个方法，并如何通过改进等策略应用到自己的研究领域中。

21.2 相关技术介绍

从题目中可以看出核心两个技术：transformer 以及 关联差异（ASSOCIATION DISCREPANCY），接下来我们把这个背景技术做最简单的梳理。

21.2.1 transformer

Transformer 是一种神经网络模型，用于处理序列数据。它的核心是自注意力机制，通过对输入序列中的元素进行自适应的关注，从而捕捉元素之间的相互作用。相比传统的循环神经网络，Transformer 可以并行计算，更好地捕捉长距离依赖关系，并具有更好的建模能力。它在自然语言处理等领域取得了重要的突破，成为了现代深度学习中的重要模型之一。

简单来说，Transformer 模型由编码器和解码器组成，每个部分由多个层堆叠而成。编码器将输入序列中的每个元素进行编码，而解码器则根据编码器的输出和上一步的预测，逐步生成输出序列。

Transformer 模型的核心是自注意力机制。自注意力机制允许模型对输入序列中的不同位置进行自适应地关注，从而捕捉元素之间的相互作用。具体而言，自注意力机制通过计算每个位置与其他位置之间的注意力权重，将每个位置的特征与其他位置的特征进行加权组合。这样，模型可以同时考虑到序列中所有位置的信息，而不仅限于局部上下文。

21.2.2 关联差异（ASSOCIATION DISCREPANCY）

“ASSOCIATION DISCREPANCY”（关联差异）是指正常时间序列和异常时间序列之间在关联性方面的差异。

具体而言，作者使用 transformer 模型来学习时间序列数据中的内在关联关系 —— transformer编码器能够捕捉序列中不同位置之间的关联信息。在训练过程中，正常时间序列和异常时间序列被编码为特征向量序列，分别输入到Transformer编码器中。

通过编码器，正常序列和异常序列会被映射到一个共享的表示空间中。然后，作者引入了关联差异损失函数来度量这两类序列之间的关联差异。关联差异损失函数计算了正常序列和异常序列的编码结果之间的差异，从而推动模型学习如何区分正常和异常序列。

通过最小化关联差异，模型被训练成能够更好地区分正常和异常时间序列，即正常序列和异常序列在关联性方面存在明显的差异。

因此，在这篇论文中，“ASSOCIATION DISCREPANCY”（关联差异）是用来度量正常时间序列和异常时间序列之间在关联性方面的差异，并通过最小化这种差异来实现时间序列异常检测。

21.3 核心方法

这里我们跳过了相关工作等部分内容，直接关注论文核心，即论文提出的是什么模型，什么方法，解决什么问题，至于效果如何下个章节我们介绍实验评估结果。

21.3.1 方法总括

论文的核心方法是提出了一种名为 “Anomaly Transformer” 的模型，利用关联差异来实现时间序列数据的异常检测目标。

Anomaly Transformer模型的核心方法包括以下步骤：

1. 数据表示：

   • 时间序列数据被转换为多维特征向量序列作为输入。
   • 特征提取过程可以使用各种方法，如滑动窗口采样、傅里叶变换等，以获取适当的特征表示。

2. Transformer编码器：

   • 特征向量序列通过Transformer编码器进行建模。
   • Transformer编码器是一个由多个自注意力层和前馈神经网络层组成的模块，用于捕捉序列中不同位置之间的关联关系。
   • 自注意力机制允许模型自动关注序列中不同位置的相关信息，以建立全局上下文表示。

3. 关联差异损失函数：

   • 引入了关联差异损失函数来度量正常序列和异常序列之间的关联差异。
   • 关联差异损失函数比较了正常序列和异常序列在编码器输出上的相似性和差异性。
   • 通过最小化关联差异，模型被训练成能够区分正常和异常时间序列。

4. 异常检测：

   • 使用经过训练的Anomaly Transformer模型对新的时间序列数据进行异常检测。
   • 输入序列经过编码器后，计算关联差异得分来评估序列中是否存在异常。
   • 高关联差异得分表明序列中存在异常，低关联差异得分表示序列正常。

通过以上方法，Anomaly Transformer模型能够学习时间序列数据中的关联关系，并利用关联差异来区分正常序列和异常序列，从而实现时间序列异常检测的任务。该模型在实验中展现了较好的性能，具有较高的准确性和鲁棒性。

21.3.2 模型架构

论文中图 1 是 Anomaly Transformer 模型的结构示意图，如上所示，其中浅蓝色方框表示 self-attention 层，黄色方框表示 feedforward 前馈层，白色方框表示 Anomaly Attention 模块，蓝色实线表示新引入的 Anomaly-Attention 机制。可以看出，Anomaly Transformer 模型由多个 Anomaly-Attention 模块和 feed forward 前馈层交替连接而成，每个模块包括了两个分支，其中一条分支是处理序列先验的 self-attention 序列，而另一条分支用于学习序列的关系。Anomaly-Attention 机制采用多层量化和对称 K-L 散度设计建立并优化了序列的关系。整个模型的输入是一个时间序列，输出是一个代表时间序列中每个时间步的异常概率值的向量。

Anomaly Attention 模块包括两个重要的计算部分：Multi-head Attention 和 MatMul。具体而言，MatMul 指的是两个输入矩阵相乘的操作，其中一个输入矩阵是通过 Multi-head Attention 计算得出，另一个输入矩阵包含了序列先验信息，用于计算当前时间步与其他时间步的关系。在 Anomaly Transformer 中，MatMul 的作用是将先验信息与自注意力矩阵相乘，从而获得增强的关系表示。这样，在之后的计算中，就可以更好地识别序列中的异常点，并得出更准确的异常概率值。

在图1的白色方框中，Anomaly Attention 模块的另一个分支包含了一个名为 “MatMul” 的操作（也就是图1下方）。该操作也是指两个输入矩阵的相乘，其中一个输入矩阵是通过自注意力计算得到的，表示序列在当前时间步的特征表示，而另一个输入矩阵是用来计算序列先验关系的，也就是序列中所有时间步之间的关系图表示。这个操作的目的在于获得更加强化的序列关系表达，并且更好的识别异常点，提高模型的性能表现。通过 Anomaly Attention 模块，模型可以同时学习自注意力和序列先验关系，并将它们结合起来以得出更准确的异常概率值。

在图1的右侧，是一个简单的全连接神经网络层。该层将经过 Self-Attention 和 Feedforward 两个模块后的序列特征进行线性变换和非线性激活，将其映射到一个低维向量空间中得到最终的输出结果。具体而言，该层的输入是一个维度为 d_model 的向量序列，其中每个时间步的向量表示自注意力模块输出的特征向量。全连接层由两个线性变换和一个激活函数组成，其中第一个线性变换作用于每个时间步的向量独立地，将其映射到一个更小的维度中。第二个变换将所有的时间步向量减少到一个单一的异常得分值。最后一个激活函数为 sigmoid 激活函数，将异常得分限制在0~1之间，代表每个时间步点为异常点的概率。整个模型的输出结果即是一个向量，其中每个维度表示对应时间点为异常的可能性得分。

21.3.3 公式计算

公式 1 Overall Architecture

结合图1，理解这个公式，第 $l$ 层的总体方程 表示为：

$$\begin{array}{rl}& {\mathcal{Z}}^l=\text{ Layer-Norm }\left(\text{ Anomaly-Attention }\left({\mathcal{X}}^{l-1}\right)+{\mathcal{X}}^{l-1}\right)\\ & {\mathcal{X}}^l=\text{ Layer-Norm }\left(\text{ Feed-Forward }\left({\mathcal{Z}}^l\right)+{\mathcal{Z}}^l\right),\end{array}\text{\hspace{1em}(1)}$$

其中， $\mathcal{Z}$ 以及 $\mathcal{X}$ 的右上角 $l$ 是用来指代网络的层级，而 $\text{ Layer-Norm}$（层归一化）是一种神经网络的归一化方法，它可以在许多机器学习应用中帮助加快训练和提高性能。

而 $\text{Feed-Forward}$ 即前馈传播是一种常见的神经网络结构，Feed-Forward Neural Network（FFN）被用于对网络的输出进行处理和转换。

公式 2 Anomaly-Attention

注意，单分支自我注意机制（Vaswani等人，2017 《Attention is all you need》）不能同时对先验关联和序列关联建模。我们提出了具有两个分支结构的 Anomaly Attention（图1）。对于先验关联，我们采用可学习的高斯核来计算相对于相对时间距离的先验。利用高斯核函数的单峰特性，本设计可以更好地关注相邻层。我们还为高斯内核使用了一个可学习的缩放参数 $\sigma$，使先验关联适应各种时间序列模式，例如不同长度的异常段。序列-关联分支是从原始序列中学习关联关系，它可以自适应地找到最有效的关联关系。请注意，这两种形式保持每个时间点的时间依赖性，这比逐点表示更具信息性。它们还分别反映了相邻集中先验和习得联想，其差异应是正常-异常可区分的：

$$\begin{array}{rl}& \text{Initialization: }\mathcal{Q},\mathcal{K},\mathcal{V},\sigma ={\mathcal{X}}^{l-1}{W}_{\mathcal{Q}}^l,{\mathcal{X}}^{l-1}{W}_{\mathcal{K}}^l,{\mathcal{X}}^{l-1}{W}_{\mathcal{V}}^l,{\mathcal{X}}^{l-1}{W}_{\sigma }^l\\ & \text{Prior-Association: }{\mathcal{P}}^l=\text{ Rescale }\left({\left[\frac{1}{\sqrt{2\pi }{\sigma }_i}\exp \left(-\frac{|j-i{|}^2}{2{\sigma }_i^2}\right)\right]}_{i,j\in \{1,\cdots ,N\}}\right)\\ & \text{Series-Association: }{\mathcal{S}}^l=\mathrm{Softmax}\left(\frac{{\mathcal{Q}\mathcal{K}}^{\mathrm{T}}}{\sqrt{d_{\text{model }}}}\right)\\ & \text{Reconstruction: }{\mathcal{Z}}^l={\mathcal{S}}^l\mathcal{V}\end{array}\text{\hspace{1em}(2)}$$

结合图 1 理解一下公式 2，核心内容包括如下图所示4个部分，首先初始化几个向量 $\mathcal{Q},\mathcal{K},\mathcal{V},\sigma$，这里的 $\mathcal{Q},\mathcal{K},\mathcal{V}$ 均来自原 attention 机制的权重向量，而 $\sigma$ 是本论文中作者提出的 “可学习的缩放参数（a learnable scale parameter）”，使先验关联是适应各种时间序列模式。

第二个等式对应下图的 2 中上面部分，也就是借助 $\sigma$ 再次调整缩放。注意从 2 到 3 的过程牵扯到的 Min Max 优化过程，在最小化阶段，先验关联最小化由高斯核导出的分布族内的关联差异。在最大化阶段，序列关联在重构损失下最大化关联差异。

通过驱动先前关联分支逼近从原始序列中学习到的序列关联分支，使先前关联分支能够适应各种时间模式。在最大化阶段，Minimize Discrepancy部分优化序列关联分支以扩大关联差异，从而迫使序列关联分支更多地关注非相邻的时间点。这样，Minimize Discrepancy部分可以使Anomaly-Attention机制更好地控制关联学习，提高异常检测的准确性。

公式 3 Association Discrepancy

Association Discrepancy 是用于计算先前关联分支和序列关联分支之间差异的指标，其公式如下：

$$\mathrm{AssDis}(\mathcal{P},\mathcal{S};\mathcal{X})={\left[\frac{1}{L}\sum _{l=1}^L\left(\mathrm{KL}\left({\mathcal{P}}_{i,:}^l\Vert {\mathcal{S}}_{i,:}^l\right)+\mathrm{KL}\left({\mathcal{S}}_{i,:}^l\Vert {\mathcal{P}}_{i,:}^l\right)\right)\right]}_{i=1,\cdots ,N}\text{\hspace{1em}(3)}$$

其中，$P$和$S$分别表示先前关联分支和序列关联分支的输出，$X$是输入的时间序列，$L$是特征层数，$N$是时间序列的长度。$P_{l,i,:}$和$S_{l,i,:}$分别表示先前关联分支和序列关联分支在第$l$层、第$i$个时间点的输出，$KL(\cdot ||\cdot )$表示KL散度，用于计算两个离散分布之间的差异。公式中的$\text{AssDis}(P,S;X)$是一个$N\times 1$的向量，表示每个时间点的关联差异。在异常检测中，较小的$\text{AssDis}(P,S;X)$值通常表示异常点。

公式 4 MINIMAX ASSOCIATION LEARNING

在最小化阶段，先验关联最小化由高斯核导出的分布族内的关联差异。在最大化阶段，序列关联在重构损失下最大化关联差异。作为一个无监督的任务，我们使用重建损失来优化我们的模型。重建损失将引导序列关联找到最具信息量的关联。为了进一步放大正常和异常时间点之间的差异，我们还使用额外的损失来放大关联差异。由于先验关联的单峰性，差异损失将引导序列关联更多地关注非相邻区域，这使得异常的重建更加困难，使得异常更易识别。输入序列 $\mathcal{X}\in {\mathbb{R}}^{N\times d}$ 的损失函数形式化为：

$${\mathcal{L}}_{\text{Total }}(\mathcal{X},\mathcal{P},\mathcal{S},\lambda ;\mathcal{X})=\Vert \mathcal{X}-\mathcal{X}{\Vert }_{\mathrm{F}}^2-\lambda \times \Vert \mathrm{AssDis}(\mathcal{P},\mathcal{S};\mathcal{X}){\Vert }_1\text{\hspace{1em}(4)}$$

公式 5

如果直接最大化关联差异将极大地降低高斯内核的尺度参数，使先验关联变得毫无意义。为了更好地控制联想学习，论文提出了一个极大极小策略（图2）。具体地，对于最小化阶段，论文驱动先验关联Pl以近似从原始序列学习的序列关联Sl。该过程将使先验关联适应各种时间模式。对于最大化阶段，论文优化了序列关联，以扩大关联差异。这一过程迫使序列-联想更加关注非相邻视界。因此，对重构损耗进行积分，两个相位的损耗函数为：

$$\begin{gathered} \text{Minimize Phase:}{\mathcal{L}}_{\text{Total }}\left(\mathcal{X},\mathcal{P},{\mathcal{S}}_{\text{detach }},-\lambda ;\mathcal{X}\right) \\ \text{Maximize Phase: }{\mathcal{L}}_{\text{Total }}\left(\mathcal{X},{\mathcal{P}}_{\text{detach }},\mathcal{S},\lambda ;\mathcal{X}\right)\text{\hspace{1em}(5)} \end{gathered}$$

其中 $\lambda >0$，${\ast }_{\text{detach}}$ 意味着停止关联的梯度反向传播（如图1所示）。在最小化阶段，$\mathcal{P}$ 近似于 ${\mathcal{S}}_{\text{detach}}$，最大化阶段将对序列关联进行更强的约束，迫使时间点更多地关注非相邻区域。在重建损失下，这对于异常比正常时间点更难实现，从而放大了关联差异的正常-异常可区分性。

公式 6

论文将归一化的关联差异的重建标准，这将采取的时间表示和可区分的关联差异的好处。最终的异常得分 $\mathcal{X}\in {\mathbb{R}}^{N\times d}$

 AnomalyScore  ( X ) = Softmax ⁡ ( − AssDis ⁡ ( P , S ; X ) ) ⊙ [ ∥ X i , : − X ^ i , : ∥ 2 2 ] i = 1 , ⋯   , N (6) \text { AnomalyScore }(\mathcal{X})=\operatorname{Softmax}(-\operatorname{AssDis}(\mathcal{P}, \mathcal{S} ; \mathcal{X})) \odot\left[\left\|\mathcal{X}_{i,:}-\widehat{\mathcal{X}}_{i,:}\right\|_2^2\right]_{i=1, \cdots, N} \tag{6}  AnomalyScore (X)=Softmax(−AssDis(P,S;X))⊙[ ​Xi,:​−X i,:​ ​22​]i=1,⋯,N​(6)

其中 $\odot$ 是逐元素乘法。异常得分 $\text{AnomalyScore}(\mathcal{X})\in {\mathbb{R}}^{N\times d}$ 表示 $\mathcal{X}$ 的逐点异常得分。为了更好的重建，异常通常会降低关联差异，这仍然会得到更高的异常分数。因此，该设计可以使重构误差和关联差异协同作用以提高检测性能。

21.4 论文实验

实验部分 https://github.com/thuml/Anomaly-Transformer 提供了比较简单的脚本方法，但这里还是稍微介绍一下使用方法。

1. clone 这个项目到本地，使用 pycharm / vscode 等工具打开这个项目。
2. 在项目的根目录下新建文件夹 dataset，并把下载好的数据集放到 dataset 目录下。如图所示：
   
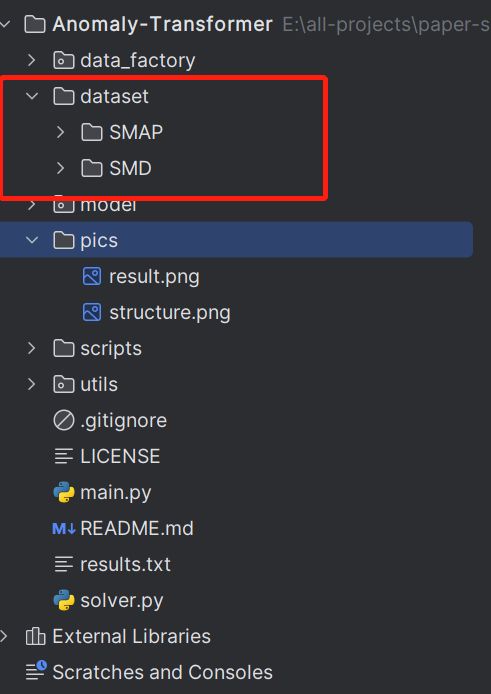
3. 运行脚本，开始训练与评估。这里可能遇到的问题我们详细介绍。

21.4.1 未安装 torch

前去 Torch 官网查看安装方法：https://pytorch.org/get-started/locally/

接着输入提示的命令即可，这个需要根据实际情况而定，不同的情况下可能对应的命令也是不同的。

21.4.2 CUDA 错误 1

RuntimeError: Found no NVIDIA driver on your system. Please check that you have an NVIDIA GPU and installed a driver from http://www.nvidia.com/Download/index.aspx

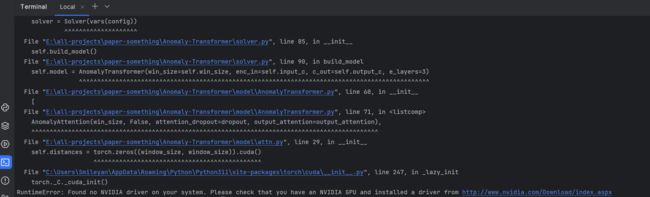这个可能是很多小伙伴们都会遇到的问题 —— 没有独立显卡，这里吐槽一下作者并没有考虑到没有GPU的贫瘠用户（比如本人）。

因为运行任务较大，这里不推荐修改代码、使用 CPU 跑算法，因为实在是太慢了。

所以这里的推荐解决方法是找有显卡的小伙伴借着用用，或者自己找个合适的平台租用一下。

21.4.3 CUDA 错误 2

RuntimeError: CUDA out of memory. Tried to allocate 80.00 MiB (GPU 0; 11.17 GiB total capacity; 10.09 GiB already allocated; 27.88 MiB free; 10.70 GiB reserved in total by PyTorch)

“算法的成本” 在论文实验中就可见一斑，10G 显存居然不够用，服了吧。我们继续加大投入，充值继续。

21.4.4 执行成功 SMD 数据集

如下图所示，执行完成后，f1-score 为 0.9027。


torch 版本以及显卡信息如下：

21.5 总结

建议先有一定的深度学习基础，然后了解一下注意力机制，学习一下 tranformer 模型基本原理，也可以去跑一跑一些开源的代码，了解了解即可。然后再看看论文，理一下论文的总体结构，大致跑一跑模型。对于自己而言，论文至少有三个地方值得学习：论文思路（结合transformer与Association Discrepancy）；处理好的数据集可以直接下载并使用；开源，提供Script脚本运行方便。

当然，对于没有实验室资源的人来说，受到了很多资源限制就比较难受，无法进行实验的话就大致梳理总体流程吧。

Smileyan
2023.06.20 21:30