数字图像处理【10】直方图反向投影与模板匹配

本篇简单描述直方图在图像处理中典型的应用场景，属于是比较老旧的应用技术，但不妨拿出来再学习，温故而知新，为新知识做一个铺垫。

直方图反向投影（Back Projection）

还记得之前学习过的图像直方图的计算/均衡化的知识吗，反向投影是在这基础上展开，需要回顾的同学可以看看这里的文章。

首先说说直方图反向投影的概念：

• 反向投影就是利用源图像的直方图模型中的分布情况/概率值，在源目标图像位置进行一个投影，通常用HSV色彩空间的H通道的直方图模型进行投影。

Note：注意这里是用HSV色彩空间，与之前介绍的HSI颜色模型有点区别。这里简单概括一下：其实它两本质是同一套理论。为什么一个叫色彩空间，一个颜色模型，最本质的区别是V和I不同，V指的是value，V=max(R,G,B)，HSV只有下半个圆锥，中轴线是灰度，HSV中纯白的那一点的位置对应在HSI中是中轴中值灰度的位置。如果说HSV的饱和度是对纯白而言的，则HSI的饱和度是对纯中值灰度而言的。由于两种模型中的I和V的不同导致了H和S的不同。在HSV色彩空间里，H的取值范围是[0~180]，S和V是[0~255]【PS：Windows电脑自带的画图软件中的调色板是HSI模型的】

为了加深理解，举个应用例子，给大家说明白什么是直方图反向投影：

(1) 例如一4x4图像的灰度如下 ：
 Image= 0    1    2    3
              4    5    6    7
              8    9   10   11
              8    9   14   15

(2) 定义该直方图的灰度区间为[0,3)，[4,7)，[8,11)，[12,16)
 则其直方图：Histogram = 4    4    6    2
 归一化后为：Histogram = 0.25    0.25    0.375    0.125

(3) 直方图反向投影后，位置(0,0)上的像素值为0，对应的bin为[0,3)，所以反向直方图在该位置上的值这个bin的值4。
 Image_BackProjection=
                      4    4    4    4
                      4    4    4    4
                      6    6    6    6
                      6    6    2    2

我们看到，实际上是原图像的256个灰度值被置为很少的几个值了，具体有几个值，那要看把0~255的灰度等级划分为多少个区间（HSV空间的H，那就是将0~180划分区间）在反向投影的特征矩阵中，具体位置的值就是它对应的原图像中的点所在区间的灰度直方图值。所以我们可以看出，一个区间点越多，在反向投影矩阵中就越亮。

从这个过程也可以看出，我们是先求出原图像的直方图，再由直方图得到反向投影得出特征矩阵，由直方图到投影矩阵实际上就是一个反向的过程，所以叫反向投影。

直方图反向投影-opencv-4.5.5 C工程实现

#include 
#include 

using namespace cv;
using namespace std;

void Hist_And_BackProjection(int, void*);
Mat src, hsv, hue;
string titleStr = "test backProjection ";
int hist_bins = 12;
int main()
{
    //读取测试图片
    src = imread("F:\\other\\learncv\\ic_launcher.png");
    namedWindow(titleStr + "src", WINDOW_KEEPRATIO);
    imshow(titleStr + "src", src);
    //rgb转hsv
    cvtColor(src, hsv, COLOR_BGR2HSV);

    hue.create(hsv.size(), hsv.depth());
    //从灰度图图像中拷贝0通道到 直方图输入图像的0通道
    int nchannels[] = { 0, 0 };
    mixChannels(&hsv, 1, &hue, 1, nchannels, 1);

    //动态调整直方图的 bins ，并做反向投影
    createTrackbar("Histogram Bins", titleStr + "src", &hist_bins, 180, Hist_And_BackProjection);
    Hist_And_BackProjection(0, 0);

    waitKey(0);
    return 0;
}

void Hist_And_BackProjection(int, void*) 
{
    float range[] = { 0,180 };
    const float* histRanges = { range };
    Mat hist;
    // 直方图计算及归一化处理
    calcHist(&hue, 1, 0, Mat(), hist, 1, &hist_bins, &histRanges, true, false);
    normalize(hist, hist, 0, 255, NORM_MINMAX, -1, Mat());

    //画直方图的分布图
    int hist_h = 400;
    int hist_w = 400;
    int bin_w = hist_w / hist_bins;
    Mat histImage(hist_w, hist_h, CV_8UC3, Scalar(255, 255, 255));
    for (int i = 1; i <= hist_bins; i++)
    {
        rectangle(histImage,
            Point((i - 1) * bin_w, (hist_h - cvRound(hist.at(i - 1) * (400 / 255)))),
            Point(i * bin_w, hist_h),
            Scalar(85, 85, 85),
            -1);
    }
    imshow(titleStr + "Histogram", histImage);

    //直方图反向投影
    Mat backPrjImage;
    calcBackProject(&hue, 1, 0, hist, backPrjImage, &histRanges, 1, true);
    namedWindow(titleStr, WINDOW_FREERATIO);
    imshow(titleStr, backPrjImage);
}

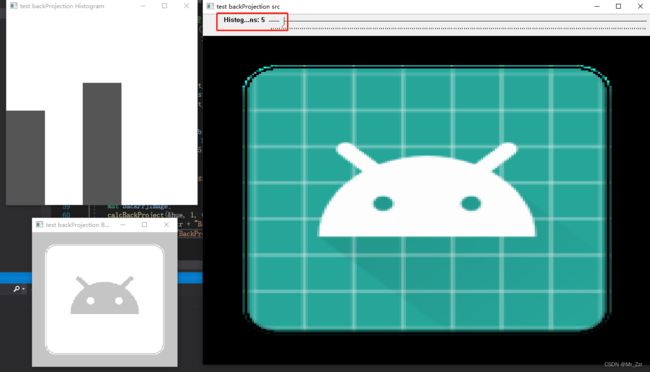
如例子所示，控制直方图区间数为5的时候，反向投影基本能提取出输入图像的特征，这里测试的输入图像比较简单，反向投影出来的特征图并没有噪点，如果有一些额外的噪点，可以利用之前学习的膨胀/腐蚀操作来掩盖掉。

模板匹配（Template Match）

接下来简单介绍opencv当中的模板匹配。还是先进行文字介绍：

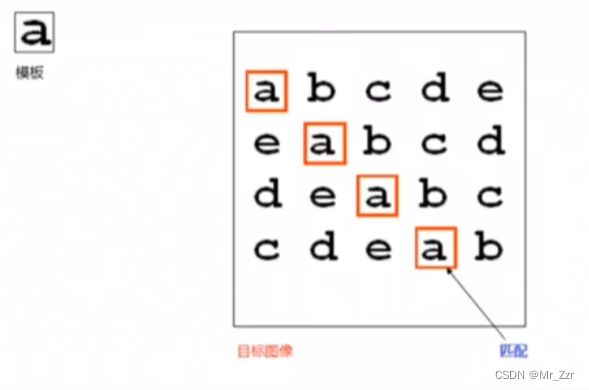
1. 模板匹配就是在目标图像的整个区域发现与给定子图像匹配的小块区域
2. 模板匹配首先得需要一个模板图像T（重点就在这个模板T，很重要！！！）
3. 在待检测的目标图像上，从左到有，从上往下计算模板图像与子图像匹配的相似程度，相似程度越大，两者内容对等的可能性越大。

 先介绍下opencv相关API——matchTemplate

cv::matchTemplate(

InputArray image,// 源图像，必须是8-bit或者32-bit浮点数图像

InputArray templ,// 模板图像，类型与输入图像一致

OutputArray result,// 输出结果，必须是单通道32位浮点数,假设源图像WxH,模板图像wxh,
                   // 则结果必须为W-w+1, H-h+1的大小。
int method, //匹配相似性的方法标识

InputArray mask=noArray()
)

第三个输出参数，OutputMat的大小是（W-w+1, H-h+1）因为模板匹配是在待检测的目标图像上，从左到有，从上往下计算模板图像与子图像，然后把相似程度输出到对应的位置中。

然后就是着重来学学 模板匹配的相似性有哪些方法：

模板匹配的核心思想就是从模板图像中，找出一个合适的指标来衡量模板T与搜索区域 I 的相似度。就好譬如小学学习的两个三角形是否相似，所以相似性又演变成以上几组数学关系。

其中的（x', y'）代表的是模板T的位置，（x,y）代表的是目标图像 I 的区域起始位置，那么 I(x+x',y+y') 的意思其实就是根据目标图像的以（x,y）为起点，偏移（x', y'）的位置。R(x,y)就是以(x,y)为起点位置，(x',y')大小的区域图像，与模板的相似程度。

• TM_SQDIFF/TM_SQDIFF_NORMED：差值平方和 / 归一化差值平方和

通过计算模板与搜索区域中所有对应位置像素点的像素平方差之和，来衡量两者相似度，计算结果越小表示越相似，当计算结果为0时表示两者完全相同。

• TM_CCORR / TM_CCORR_NORMED：相关系数 / 归一化相关系数

采用T和I的相关系数作为衡量指标，相关系数越大表示两者越相似。

• TM_CCOEFF / TM_CCOEFF_NORMED：去均值相关系数 / 去均值归一化相关系数

去均值相关系数与相关系数的区别在于：计算去均值相关系数时T和I都减去各自的均值，而相关系数则不减去均值。这样做是为了消除T和I亮度不同对计算结果的影响，比如T和I的结构非常相似但亮度有很大区别，那么它们分别减去各自的均值，使用每个像素点的亮度偏移来计算，而不是使用亮度本身来计算，因此消除了亮度不同的影响。
 

细心的同学可能会发现，起始模板匹配存在明显的缺点，或者说使用模板匹配会存在很多前置的限制条件：

1、模板的尺寸固定，在目标图像搜索出来的区域就是和模板尺寸一样大，并不能智能识别出不同大小的相似特征区域，在不同大小的目标图像区域，即使相同的相似度算法，也会导致完全不一样结果。

2、目标图像如果存在旋转、缩放、局部非刚性形变的情况下，模板匹配的效果也是不太好。或者说需要对模板图也进行旋转、缩放、局部非刚性形变等操作后，才能使用模板匹配。