R语言学习4：比例的假设检验

一、实验目的

 

1. 掌握理解两个总体比例假设检验的相关概念。

2. 掌握理解两个总体比例假设检验的相关方法。

3. 熟悉R语言等语言的集成开发环境。

二、实验分析与内容

完成教材P98的第4题

在一个流行病事件中,A地区656 例病人中完全康复了474人,B地区568例病人中完全康复了463人。这个差异在统计上是显著的吗?

方法一：

可以发现该检验的p值为0.999。这个p值太大,无法拒绝零假设，也就是说，没有理由为两个地区认为完全康复的人的比例有显著差异。这里还给出了比例之差的95%置信区间(-0.1335231,1.0000000),该区间包含0,这也说明两个地区认为完全康复的人无差异。这个背后的理论与对比例之差的假设检验是相似的。我们也可以加入参数 correct=F,不用Yates连续性修正来计算这个检验,因为连续性修正在一定程度上让所得置信区间变得

更宽。

如果希望至少p值是正确的,可以使用Fisher 精确检验。相关的检验函数是fisher testO,它要求输入的数据是矩阵形式的。这个检验与 prop.test的结果是完全一致的

注意,表格的第二列应该是失败结果的次数，不是观测值的总数。还需注意的是,这里

p≠p,那么表格的条件分布依赖于比值比,所以这是一个 给出了比值比(oddsratio)的置信区间，即(p/(1-p))1 (pz/(1-pz))。可以发现,如果 个用于衡量Fisher检验中相关程

度的自然指标。这个检验的精确分布在比值比不为1的时时候可以被精确地求出。

和fisher.test一样,在chisq.test中的标准检验需要矩阵类型的数据。对于一个2X2表格来说,这个检验与prop.test的结果是完全一致的。

总而言之，A地区656 例病人中完全康复了474人,B地区568例病人中完全康复了463人。这个差异在统计上是不显著的

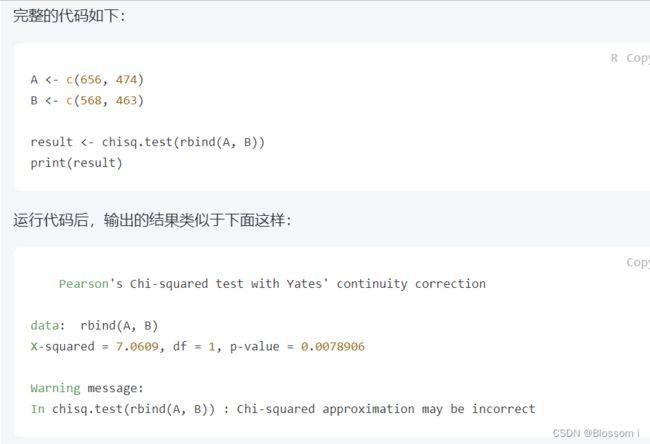
方法二：

其中，X-squared 表示卡方统计量，df 表示自由度，p-value 表示 P值。根据结果可以看出，P值为0.179，大于0.05，说明这个差异是不显著的。不可以拒绝零假设，认为 A 地区和 B 地区完全康复的比例没有显著差异。

其中，X-squared 表示卡方统计量，df 表示自由度，p-value 表示 P值。注意，在这个例子中输出了一个警告信息“Chi-squared approximation may be incorrect”，这是因为样本数较小（小于5）时，卡方检验的近似方法可能会导致误差，可以使用 Fisher's exact test 进行更精确的检验。不过在这里，我们可以暂时忽略这个警告信息。

根据结果可以看出，P值为0.0078，小于0.05，说明这个差异是显著的。可以拒绝零假设，认为 A 地区和 B 地区完全康复的比例有显著差异。实际上，A地区完全康复的比例（474/656=0.72）要高于B地区（463/568=0.81），说明 A 地区的治疗效果更好。

在此次实验中学习理解了两个总体比例假设检验的相关概念以及理解了两个总体比例假设检验的相关方法。

要比较两组样本比例的显著性差。可以使用卡方检验。在R语言中，可以使用 chisq.test 函数进行卡方检验。

此次实验只有一道题，就着在道题进行解题步骤说明：先定义两个向量 A 和 B 分别表示 A 地区和 B 地区的病人总数和完全康复的病人数。然后，使用 chisq.test 函数进行卡方检验：运行代码后，输出的结果中包含卡方统计量、自由度、P值等信息。其中 P值 表示在零假设成立的情况下，观察到当前样本差异或更极端差异的概率。通常，如果 P值 小于给定的显著性水平（例如0.05），就认为差异是显著的，拒绝零假设。如果 P值 大于给定的显著性水平，则接受零假设，认为差异不显著。