数据结构 树
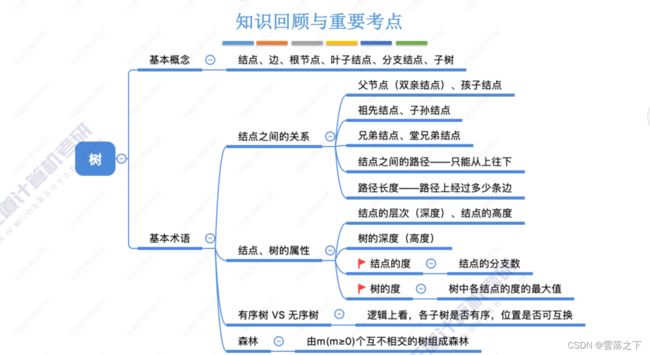
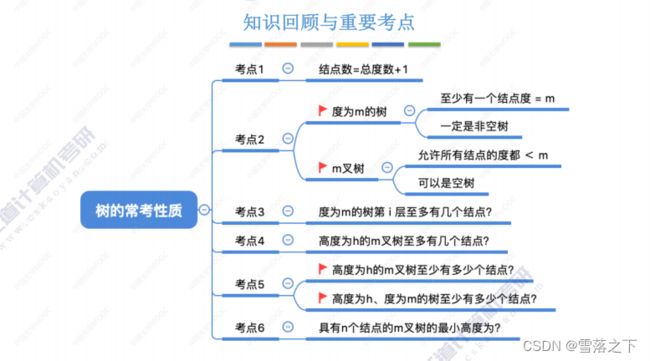
树的基本概念
树是一种非线性的数据结构,它由节点(node)和边(edge)组成。树的基本概念包括以下要点:
- 树由一个根节点(root)开始,根节点没有父节点,它可以有零个或多个子节点。
- 每个节点可以有零个或多个子节点,子节点之间没有顺序关系。
- 除了根节点之外,每个节点有且仅有一个父节点。
- 如果一个节点没有子节点,它被称为叶节点(leaf)或终端节点(terminal node)。
- 节点之间的连接线称为边,边表示节点之间的关系。
树具有层次性的结构,节点和边的关系形成了树的拓扑结构。
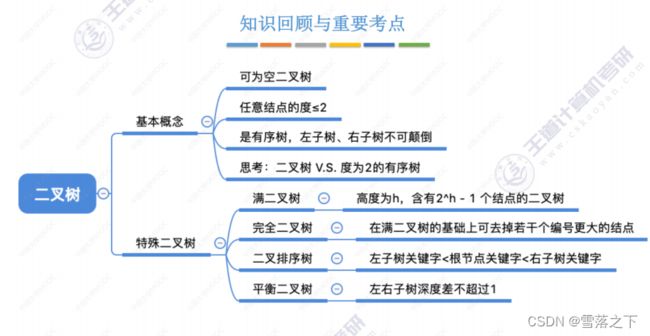
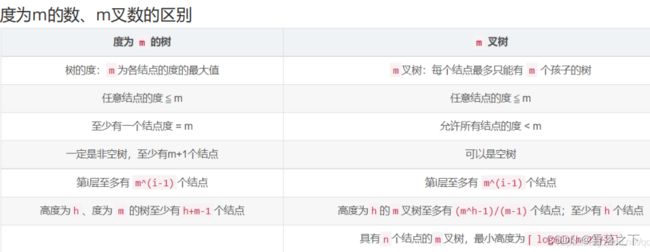
二叉树的基本概念与逻辑结构
二叉树是一种特殊的树结构,其中每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树的基本概念包括以下要点:
- 每个节点最多有两个子节点,分别称为左子节点和右子节点。
- 二叉树中的子树也是二叉树,且子树的位置可以是左子树或右子树。
- 二叉树的子节点没有顺序关系,即左子节点和右子节点可以互换位置而得到相同的二叉树。
二叉树的逻辑结构可以用递归方式定义为一个节点加上两个二叉树的集合,即:
二叉树 = 节点 + 左子树 + 右子树
二叉树的存储结构
二叉树的存储结构主要有两种方式:链式存储和顺序存储。
-
链式存储:每个节点使用一个包含数据和指向左右子节点的指针的结构体来表示。通过指针将各个节点连接起来,形成一个链式结构。链式存储灵活,适用于任意形状的二叉树。
-
顺序存储:使用数组来表示二叉树的节点,按照层次遍历的顺序存储节点的数据。对于某个节点的索引为i,它的左子节点的索引为2i,右子节点的索引为2i+1。顺序存储简单高效,适用于完全
二叉树。
操作 1:遍历二叉树
遍历二叉树是指按照一定规则访问二叉树的所有节点,常用的遍历方式有三种:
- 前序遍历(Preorder Traversal):先访问根节点,然后递归地遍历左子树,最后递归地遍历右子树。
- 中序遍历(Inorder Traversal):先递归地遍历左子树,然后访问根节点,最后递归地遍历右子树。
- 后序遍历(Postorder Traversal):先递归地遍历左子树,然后递归地遍历右子树,最后访问根节点。
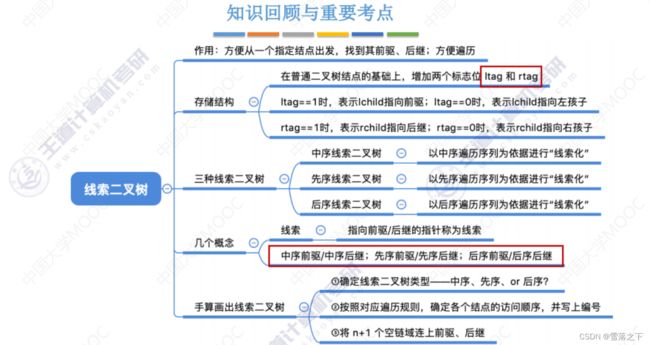
操作 2:线索二叉树
线索二叉树是在二叉树的基础上,利用空指针的空闲域或者指针域指向前驱节点或后继节点,形成一种特殊的二叉树结构。
- 前序线索二叉树:在前序遍历的过程中,将遍历的路径上的空指针指向前驱或后继节点。
- 中序线索二叉树:在中序遍历的过程中,将遍历的路径上的空指针指向前驱或后继节点。
- 后序线索二叉树:在后序遍历的过程中,将遍历的路径上的空指针指向前驱或后继节点。
线索二叉树可以提高遍历二叉树的效率,可以快速找到一个节点的前驱节点或后继节点。
操作 3:哈夫曼树及其应用
哈夫曼树是一种特殊的二叉树,常用于数据压缩和编码算法中。哈夫曼树的特点是权值较大的节点离根节点较近,权值较小的节点离根节点较远。
构建哈夫曼树的步骤:
- 将所有节点按照权值从小到大进行排序。
- 取出权值最小的两个节点作为左右子节点,构建一个新的父节点,父节点的权值为左右子节点的权值之和。
- 将新构建的父节点插入原节点集合中,并删除原来的两个子节点。
重复步骤2和3,直到节点集合中只剩下一个根节点为止。
哈夫曼树的应用主要是通过构建哈夫曼树来实现数据的压缩和解压缩,使得压缩后的数据占用更少的存储空间。
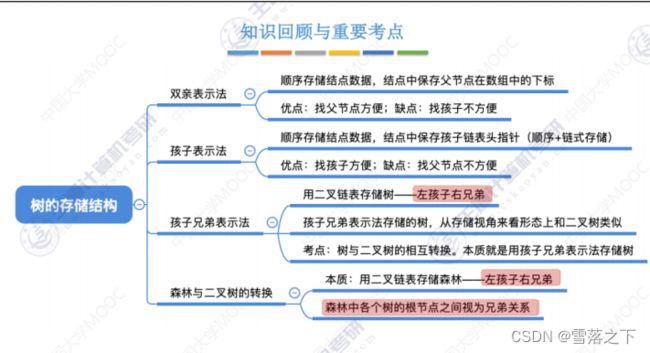
操作 4:二叉树、树和森林相互转换
- 二叉树转换为树:对于任意一个节点的左子节点,将它的右子节点作为它的兄弟节点,然后将其转化为树结构。
- 树转换为二叉树:对于任意一个节点的兄弟节点,将它的右兄弟节点作为它的右子节点,然后将其转化为二叉树结构。
- 森林转换为二叉树:将森林中的每个树转换为二叉树,然后将它们连接起来形成一个二叉树结构。
- 二叉树转换为森林:将二叉树中的每个子树转换为树结构,然后将它们分离开形成森林。
这些转换操作可以通过调整节点的指针关系来实现,从而在二叉树、树和森林之间相互转换。
操作实例
树的操作
当涉及到树的常见操作时,以下是一些常见的操作及其相应的C语言代码示例。我将逐行分析这些代码,以帮助您理解每个操作的含义和实现细节。
- 定义树节点结构
struct TreeNode {
int data; // 存储节点数据
struct TreeNode* left; // 指向左子节点的指针
struct TreeNode* right; // 指向右子节点的指针
};
这段代码定义了一个树节点结构,其中包含一个整型数据和两个指针,分别指向左子节点和右子节点。
- 创建新节点
struct TreeNode* createNode(int data) {
struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
newNode->data = data;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
这段代码创建一个新的树节点,并将给定的数据赋值给节点的data字段。然后,将左右子节点指针初始化为NULL,最后返回新创建的节点指针。
- 插入节点
struct TreeNode* insertNode(struct TreeNode* root, int data) {
if (root == NULL) {
root = createNode(data);
} else if (data <= root->data) {
root->left = insertNode(root->left, data);
} else {
root->right = insertNode(root->right, data);
}
return root;
}
这段代码用于向树中插入一个新节点。它接受一个根节点指针和要插入的数据作为参数。首先,它检查根节点是否为NULL,如果是,则创建一个新节点并将其设置为根节点。否则,它比较要插入的数据与当前节点的数据大小关系,然后递归地将新节点插入到左子树或右子树中。最后,返回更新后的根节点指针。
- 查找节点
struct TreeNode* searchNode(struct TreeNode* root, int data) {
if (root == NULL || root->data == data) {
return root;
} else if (data < root->data) {
return searchNode(root->left, data);
} else {
return searchNode(root->right, data);
}
}
这段代码用于在树中查找具有给定数据的节点。它接受一个根节点指针和要查找的数据作为参数。首先,它检查根节点是否为NULL或者当前节点的数据是否与要查找的数据相等。如果是,则返回当前节点指针。否则,它比较要查找的数据与当前节点的数据大小关系,然后递归地在左子树或右子树中查找。如果找到匹配的节点,则返回该节点指针;否则,返回NULL表示未找到。
- 删除节点
struct TreeNode* deleteNode(struct TreeNode* root
, int data) {
if (root == NULL) {
return root;
} else if (data < root->data) {
root->left = deleteNode(root->left, data);
} else if (data > root->data) {
root->right = deleteNode(root->right, data);
} else {
if (root->left == NULL && root->right == NULL) {
free(root);
root = NULL;
} else if (root->left == NULL) {
struct TreeNode* temp = root;
root = root->right;
free(temp);
} else if (root->right == NULL) {
struct TreeNode* temp = root;
root = root->left;
free(temp);
} else {
struct TreeNode* minRight = findMin(root->right);
root->data = minRight->data;
root->right = deleteNode(root->right, minRight->data);
}
}
return root;
}
这段代码用于从树中删除具有给定数据的节点。它接受一个根节点指针和要删除的数据作为参数。首先,它检查根节点是否为NULL。如果是,则返回NULL。然后,它比较要删除的数据与当前节点的数据大小关系,并递归地在左子树或右子树中删除目标节点。如果要删除的节点是叶子节点,则直接释放该节点的内存并将指针设置为NULL。如果要删除的节点只有一个子节点,则将子节点的指针赋值给当前节点,并释放当前节点的内存。如果要删除的节点有两个子节点,则首先找到右子树中的最小节点,并将该节点的数据复制到当前节点。然后,递归地在右子树中删除该最小节点。最后,返回更新后的根节点指针。
- 查找最小值
struct TreeNode* findMin(struct TreeNode* root) {
if (root == NULL) {
return NULL;
} else if (root->left == NULL) {
return root;
} else {
return findMin(root->left);
}
}
这段代码用于在树中查找最小值节点。它接受一个根节点指针作为参数。首先,它检查根节点是否为NULL。如果是,则返回NULL。然后,它检查当前节点的左子节点是否为NULL。如果是,则当前节点为最小值节点,返回当前节点指针。否则,递归地在左子树中查找最小值节点。
这些是树的常见操作的C语言代码示例,以及对每行代码的分析。通过理解这些代码,您可以更好地理解树数据结构的基本操作和实现方式。
二叉树的操作
当涉及到二叉树的常见操作时,以下是一些常用的C语言代码示例,并附有逐行分析:
#include 逐行分析:
#include和#include:这些是C标准库的头文件,分别包含了标准输入输出和动态内存分配函数。struct Node:定义了二叉树的节点结构。它包含一个整数数据(data)和两个指向左子节点(left)和右子节点(right)的指针。createNode():创建一个新的二叉树节点。它分配了一个新的struct Node结构的内存,并设置数据和指针的初始值,然后返回该节点的指针。insertNode():插入一个节点到二叉树中。它接收一个指向根节点的指针(root)
和要插入的数据(data)。根据数据的大小,递归地将节点插入左子树或右子树中。
5. preorderTraversal()、inorderTraversal()和postorderTraversal():分别实现了二叉树的先序、中序和后序遍历。它们通过递归调用自身来遍历二叉树,并在访问每个节点时打印节点的数据。
6. main():主函数。它创建一个空的二叉树根节点(root),然后插入一些节点到二叉树中。最后,它调用三种遍历函数,并打印遍历结果。
这些代码展示了如何使用C语言实现二叉树的创建、插入和遍历操作。你可以根据需要进一步扩展和修改这些代码以满足其他操作的要求。
线索二叉树
下面是线索二叉树常见操作的C语言代码,每行后面有相应的注释进行分析。
#include 现在逐行进行代码分析:
#include:包含标准输入输出的头文件。#include:包含标准库函数的头文件。- 定义了表示线索二叉树节点的结构体
struct TreeNode,包含了节点的数据data、左子节点指针left、右子节点指针right,以及表示线索的标志位leftThread和rightThread。 createNode函数用于创建新的节点,接受一个整数作为节点的数据。在堆上分配内存空间,然后设置节点的初始值,并返回指向新节点的指针。insertLeft函数用于在指定节点的左侧插入子节点,接受父节点和子节点的指针作为参数。函数会将子节点插入到父节点的左侧,并设置相关的线索标志位。如果子节点的左子树不为空,需要找到最右边的叶子节点,将其右指针指向子节点。insertRight函数用于在指定节点的右侧插入子节点,接受父节点和子节点的指针作为参数。函数会将子节点插入到父节点的右侧,并设置相关的线索标志位。如果子节点的右子树不为空,需要找到最左边的叶子节点,将其左指针指向子节点。inorderTraversal函数用于中序遍历线索二叉树并按升序输出节点的数据。接受根节点的指针作为参数。函数中使用了两个指针current和temp,current初始指向根节点最左边的叶子节点,然后按中序遍历的规则遍历线索二叉树,并输出节点的数据。temp用于在遍历右子树时,找到右子树最左边的叶子节点。main函数作为程序的入口点。在这里进行测试。创建了根节点和其他节点,并通过调用insertLeft和insertRight函数构建线索二叉树。最后调用inorderTraversal函数中序遍历线索二叉树并输出结果。- 返回 0,表示程序执行成功结束。
哈夫曼树
下面是一个哈夫曼树(Huffman Tree)的常见操作的C语言代码,附带逐行分析注释:
#include 代码分析:
- 首先,我们包含了需要的标准库头文件
stdio.h和stdlib.h。 - 定义了哈夫曼树的结点结构体
struct Node,包含了数据成员data、left和right,分别表示结点的值、左子树和右子树。 - 创建一个新的哈夫曼树结点的函数
createNode(),该函数接收一个整数参数作为结点的数据,动态分配内存并返回新的结点指针。 - 构建哈夫曼树的函数
buildHuffmanTree(),接收一个整数数组和数组大小作为参数,返回构建好的哈夫曼树的根结点指针。该函数使用循环构建哈夫曼树,具体步骤如下:- 创建一个结点数组
nodeArr[],初始化为包含给定数组元素的叶子结点。 - 循环直到只剩下一个根节点:
- 从结点数组中选择两个最小值作为左右子树。
- 创建一个新的父节点,并将最小的两个结点作为其子节点。
- 删除已经使用的两个结点,并将新的父节点插入到合适的位置。
- 返回最后剩下的根节点。
- 创建一个结点数组
- 递归方式打印哈夫曼编码的函数
printHuffmanCodes(),接收哈夫曼树的根结点指针、一个整数数组和一个整数作为参数。该函数使用递归方式遍历哈夫曼树,具体步骤如下:- 如果当前结点有左子树,则将 0 存储到数组中,并继续遍历左子树。
- 如果当前结点有右子树,则将 1 存储到数组中,并继续遍历右子树。
- 如果当前结点是叶子结点,则打印该叶子结点的数据和数组中的值(构成哈夫曼编码)。
- 主函数
main():- 定义一个整数数组
arr[],存储哈夫曼树节点的权重。 - 计算数组的大小。
- 调用
buildHuffmanTree()函数构建哈夫曼树,并将返回的根结点指针赋值给root。 - 定义一个整数数组
codes[]和一个整数变量top,用于存储哈夫曼编码。 - 打印 “Huffman Codes:”。
- 调用
printHuffmanCodes()函数打印
- 定义一个整数数组
哈夫曼编码。
- 返回 0,表示程序正常结束。