二叉树与红黑树见解
目录
- 一、红黑树简介
- 二、 红黑树的特性
- 三、红黑数的应用
- 四、红黑树的原理实现
-
- 4.1 识别红黑树
- 4.2 红黑树节点的旋转
- 4.3 插入节点
-
- 4.3.1分情况讨论:
- 4.3.2 代码示例
- 4.4删除节点
-
- 相关引用
一、红黑树简介
红黑树是一种自平衡的二叉查找树,是一种高效的查找树。红黑树具有良好的效率,它可在 O(logN) 时间内完成查找、增加、删除等操作1。
大家应该都学过平衡二叉树(AVLTree),了解到AVL树的性质,其实平衡二叉树最大的作用就是查找,AVL树的查找、插入和删除在平均和最坏情况下都是O(logn)。AVL树的效率就是高在这个地方。如果在AVL树中插入或删除节点后,使得高度之差大于1。此时,AVL树的平衡状态就被破坏,它就不再是一棵二叉树;为了让它重新维持在一个平衡状态,就需要对其进行旋转处理, 那么创建一颗平衡二叉树的成本其实不小. 这个时候就有人开始思考,并且提出了红黑树的理论,红黑树在业界应用很广泛,比如 Java 中的 TreeMap,JDK 1.8 中的 HashMap、C++ STL 中的 map 均是基于红黑树结构实现的。那么红黑树到底比AVL树好在哪里?
二、 红黑树的特性
在讲解红黑树性质之前,先简单了解一下几个概念:
parent:父节点
sibling:兄弟节点
uncle:叔父节点( parent 的兄弟节点)
grand:祖父节点( parent 的父节点)
首先,红黑树是一个二叉搜索树,它在每个节点增加了一个存储位记录节点的颜色,可以是RED,也可以是BLACK;通过任意一条从根到叶子简单路径上颜色的约束,红黑树保证最长路径不超过最短路径的二倍,因而近似平衡(最短路径就是全黑节点,最长路径就是一个红节点一个黑节点,当从根节点到叶子节点的路径上黑色节点相同时,最长路径刚好是最短路径的两倍)。它同时满足以下特性:
节点是红色或黑色
根是黑色
如果一个节点是红色,那么它的子节点必须是黑色。
从一个节点到NULL指针的每一条路径必须包含相同数目的黑色节点
三、红黑数的应用
主要就是利用红黑树的键值对(key-value)查找效率高(内存管理)和中序遍历时是顺序的
- STL中的map——>红黑树的封装
- Nginx中的应用
- 定时器(查找效率高)
- 进程的调度CFS:n个进程用红黑树来存储,这个进程集合在调度的时间,查找最小的值来调度
- 内存管理:内存中的内存块用红黑树存起来,而一块内存表述方式:1. 起始位置加内存长度,2. 起始位置和终止位置。存储方式用起始位置当做key,用一个指针指向key,分配一个内存块就往红黑树上加一个节点
四、红黑树的原理实现
4.1 识别红黑树
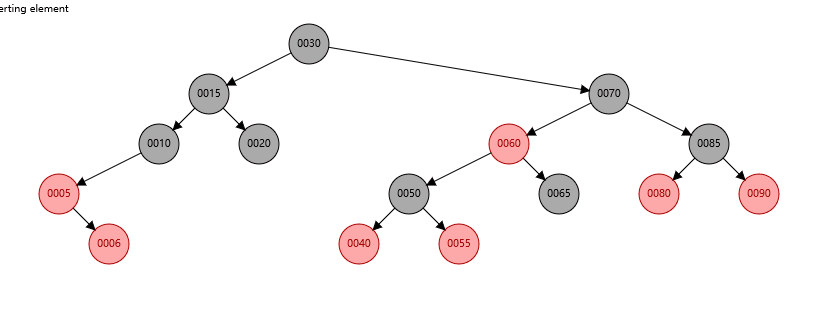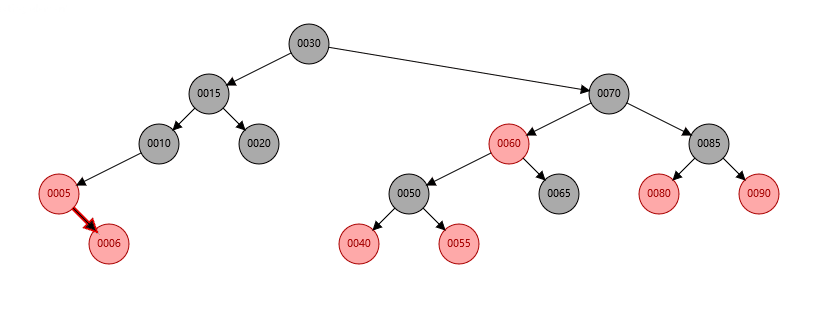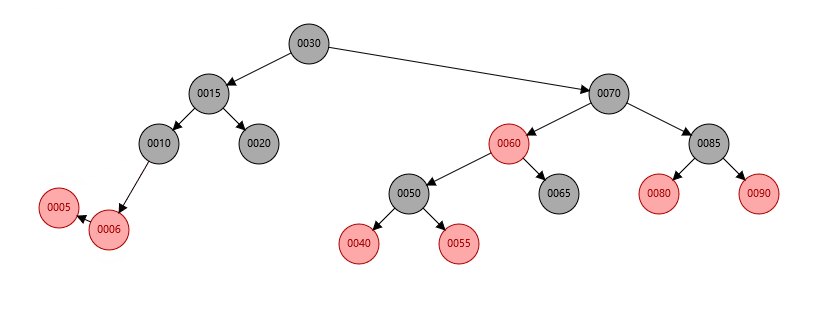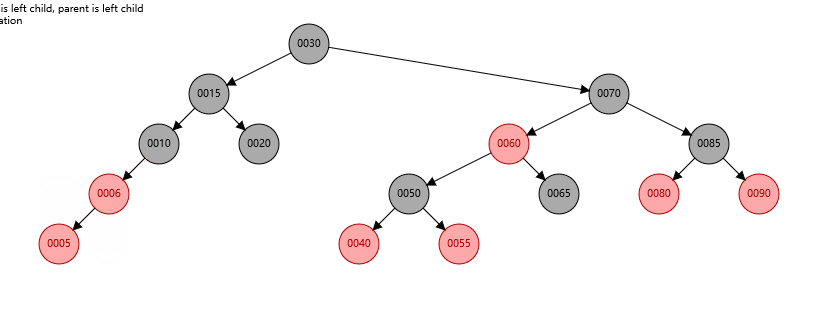
根据上面的性质,我们来判断一下下面这课树是不是红黑树
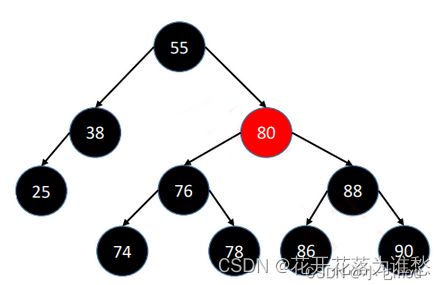
上面这棵树首先很容易就能知道是满足性质1-3条的,关键在于第4条性质,可能乍一看好像也是符合第4条的,但实际就会陷入一个误区,直接将图上的最后一层的节点看作叶子节点,这样看的话每一条从根节点到叶子结点的路径确实都经过了3个黑节点。
但实际上,在红黑树中真正被定义为叶子结点的,是那些空节点,如下图。
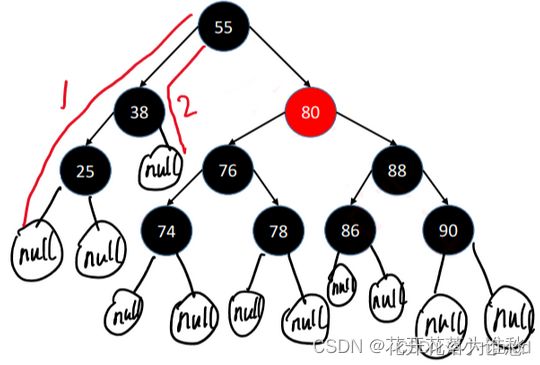
这样一来,路径1有4个黑色节点(算上空节点),路径2只有3个黑色节点,这样性质4就不满足了,所以这棵树并不是一个红黑树节点。
4.2 红黑树节点的旋转
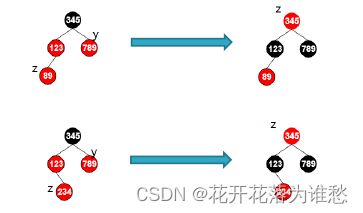
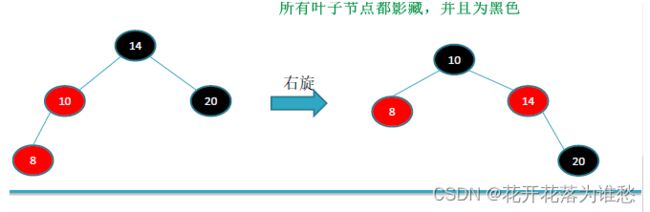
这个记忆方法特别好记:左旋就是把右孩子往上提,右旋就是把左孩子往上提

这是左旋
 这是右旋
这是右旋

这是左旋的具体细节
4.3 插入节点
4.3.1分情况讨论:
这里插入的是红色节点。(如果插入的节点,它的父节点是黑色的就直接成立,不做旋转)。
- 爸爸红,叔叔红,爸爸是左孩子(在这里,我们把父节点,叔节点和祖父节点全部变一下颜色就好了。)
2.1爸爸红,叔叔黑,爸爸是左孩子,当前结点是左孩子(先让爷爷和爸爸变一下颜色,在以爷爷为中心右旋。保证子树也是红黑树)
- 2爸爸红,叔叔黑,爸爸是左孩子,而且当前结点是右孩子,z使我们要检查的节点,y是叔叔(我们先让爸爸123左旋,在此结果上继续检查123节点,这样就变成2…1那种情况了)
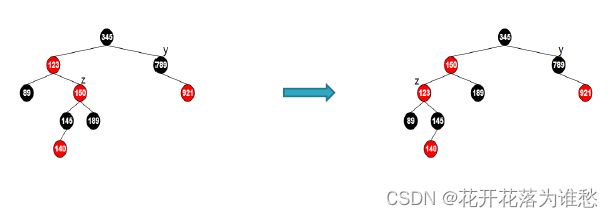
(和2.1相同,先让爷爷和爸爸变一下颜色,在以爷爷为中心右旋。保证子树也是红黑树)
如果爸爸是右孩子也是上面的两种情况。
4.3.2 代码示例
理解了以上部分就可以看下面插入节点的代码
//定义红黑树的相关内容
#define RED 0
#define BLACK 1
typedef int KEY_TYPE;
//红黑树的节点
typedef struct _rbtree_node {
//rbtree
unsigned char color;
struct rbtree_node *parent;
struct rbtree_node *left;
struct rbtree_node *right;
// end
KEY_TYPE key; //节点的键
// value
//
} rbtree_node;
//红黑树根和叶子结点
struct rbtree {
rbtree_node *root;
rbtree_node *nil; // NULL 叶子结点
};
下面的是旋转节点的代码,一定要配合前面的图来看。
// rotate
void rbtree_left_rotate(rbtree *T, rbtree_node *x) {
// NULL --> T->nil
if (x == T->nil||x->right== T->nil) return ; // 容错设置
// 第一个方向
rbtree_node *y = x->right;
x->right = y->left; //前提y不是NULL节点
if (y->left != T->nil) {
y->left->parent = x;
}
// 2
y->parent = x->parent;
if (x->parent == T->nil) { //x就是根节点
T->root = y;
} else if (x == x->parent->left) { //x是他老爸的左孩子
x->parent->left = y;
} else { //x是他老爸的右孩子
x->parent->right = y;
}
// 3
y->left = x;
x->parent = y;
}
// x --> y, y -->x
// left --> right, right --> left
void rbtree_right_rotate(rbtree *T, rbtree_node *y) {
// NULL --> T->nil
if (y == T->nil||y->left == T->nil) return ;
// 1
rbtree_node *x = y->left;
y->left = x->right;
if (x->right != T->nil) {
x->right->parent = y;
}
// 2
x->parent = y->parent;
if (y->parent == T->nil) {
T->root = x;
} else if (y == y->parent->right) {
y->parent->right = x;
} else {
y->parent->left = x;
}
// 3
x->right = y;
y->parent = x;
}
以下是插入节点的代码。一定要配合那三种情况来看
//T表示这个树的根节点,z表示插入的节点,从下往上调整
void rbtree_insert_fixup(rbtree *T, rbtree_node *z) {
// z->color == RED
// z->parent->color == RED
// z--> RED
while (z->parent->color == RED) { // z红色,z爸爸红色
if (z->parent == z->parent->parent->left) { //z的爸爸是左孩子
rbtree_node *y = z->parent->parent->right; //z的叔叔
if (y->color == RED) { //1.爸爸红,叔叔红,爸爸是左孩子
z->parent->color = BLACK; //爸爸黑
z->parent->parent->color = RED; //爷爷红
y->color = BLACK; //叔叔黑
z = z->parent->parent; //继续检查爷爷
} else { // 2.爸爸红,叔叔黑,爸爸是左孩子
if (z = z->parent->right) { // 2.1 爸爸红,叔叔黑,爸爸是左孩子,自己是右孩子
z = z->parent; // z指向爸爸
rbtree_left_rotate(T, z); //以z的爸爸为中心左旋,z现在在左下z红,z的爸爸红
}
z->parent->color = BLACK; // 2.2 爸爸红,叔叔黑,爸爸是左孩子,自己是左孩子
z->parent->parent->color = RED;
rbtree_right_rotate(T, z->parent->parent); //以z的爷爷为中心右旋,
}
} else{ //z的爸爸是右孩子
rbtree_node *y = z->parent->parent->left; //z的叔叔
if (y->color == RED) { //1.爸爸是右孩子,爸爸红,叔叔红
z->parent->color = BLACK; //爸爸黑
z->parent->parent->color = RED; //爷爷红
y->color = BLACK; //叔叔黑
z = z->parent->parent; //继续检查爷爷
} else { // 2.爸爸是右孩子,爸爸红,叔叔黑
if (z = z->parent->left) { // 2.1 爸爸红,叔叔黑,爸爸是左孩子,自己是右孩子
z = z->parent; // z指向爸爸
rbtree_right_rotate(T, z); //以z的爸爸为中心左旋,z现在在左下z红,z的爸爸红
}
z->parent->color = BLACK; // 2.2 爸爸红,叔叔黑,爸爸是左孩子,自己是左孩子
z->parent->parent->color = RED;
rbtree_left_rotate(T, z->parent->parent); //以z的爷爷为中心右旋,
}
}
}
}
void rbtree_insert(rbtree *T, rbtree_node *z) {
rbtree_node *y = T->nil;
rbtree_node *x = T->root;
while (x != T->nil) {
y = x; //y始终是x的爸爸,除特殊情况外
if (z->key < x->key) {
x = x->left;
} else if (x->key < z->key ) {
x = x->right;
} else { //Exist //相等的情况要具体分析,这里选择退出
exit(-1); //如果是定时器的话可以加一个很小的值
}
}
z->parent = y;
if (y == T->nil) {
T->root = z; //插入z前红黑树没有元素
} else if (z->key < y->key) {
y->left = z;
} else {
y->right = z;
}
// z -->
z->color = RED;
z->left = T->nil;
z->right = T->nil;
//
}
4.4删除节点
**这个我也不太会,我就直接复制了别人的思路,大家可以一起学习一下,以下是引用内容2
原文链接:https://blog.csdn.net/chenlong_cxy/article/details/121481859**
红黑树的删除要比插入更加难以理解,但是只要仔细一点也还行。
第一步:找到实际待删除的结点
找结点的过程与二叉搜索树寻找待删除结点的方法一样,若找到的待删除结点的左右子树均不为空,则需要使用替换法进行删除。因此我们最终需要删除的都是左右子树至少有一个为空的结点。
找到实际待删除结点后,先不删除该结点,否则调整红黑树时不容易控制,找到实际待删除结点后立即进行红黑树的调整。
第二步:调整红黑树
调整红黑树之前,我们先判断一下本次结点的删除是否会破坏了红黑树的性质,若破坏了我们才需要对红黑树进行调整。
若实际删除的结点是红色结点,那么本次删除操作不会破坏红黑树的性质,因此我们不需要对红黑树进行调整。反之,若删除的结点是黑色结点,我们就需要对红黑树进行调整,因为黑色结点的删除将会使得一些路径中黑色结点的数目减少,此时便破坏了红黑树的性质四。
我们先来说最简单的一种情况,即待删除结点只有一个孩子为空的情况。
在这种情况下,待删除结点要么是只有左孩子,要么是有只右孩子,但不管是左孩子还是右孩子,这个孩子一定是红色的,因为若这个孩子是黑色的,那么此时图示长蓝色路径的黑色结点数目比短蓝色路径的黑色结点数目多,不符合红黑树的性质。
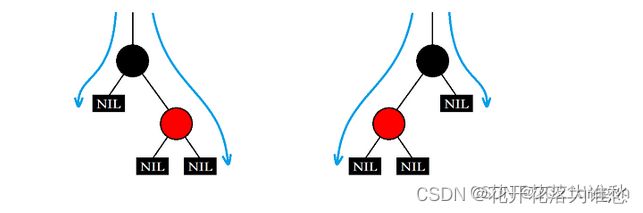
又因为红黑树当中不允许出现连续的红色结点,因此在这种情况下实际上就只有图示两种实际情况,这时我们直接将待删除结点的那个红孩子变成黑色就行了,因为在后面实际删除结点时会将这个孩子连接到删除结点的父结点下面,连接后相当于我们删除的是一个红色结点,红黑树调整完成。
下面再来说比较复杂的情况,即待删除结点的左右孩子均为空。
我们以待删除结点是其父结点的左孩子为例,分为以下四种情况:
图示说明:
若parent结点为白色,表明parent结点可能是红色结点也可能是黑色结点。
若bL或bR结点为白色,表明其可能是红色结点或黑色结点甚至该结点不存在。
bL和bR结点为黑色时,表明他们可能是黑色结点或该结点不存在。
情况一:brother为红色。
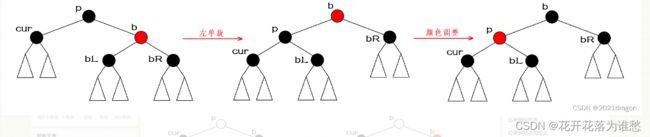 当待删除结点的brother为红色时,我们先以parent为旋转点进行一次左单旋,再将brother的颜色变为黑色,将parent的颜色变为红色,此时我们再对待删除结点cur进行情况分析,情况一就转换成了情况二、三或四。
当待删除结点的brother为红色时,我们先以parent为旋转点进行一次左单旋,再将brother的颜色变为黑色,将parent的颜色变为红色,此时我们再对待删除结点cur进行情况分析,情况一就转换成了情况二、三或四。
情况二:brother为黑色,且其左右孩子都是黑色结点或为空。
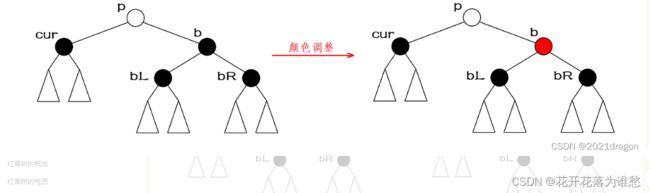 在该情况下,我们直接将brother的颜色变成红色,此时根据parent的颜色决定红黑树的调整是否结束,若parent的颜色是红色,则我们将parent变为黑色后即可结束红黑树的调整;若parent的颜色原本就是黑色,则我们需要将parent结点当作下一次调整时的cur结点进行情况分析,并且情况二在下一次调整时可能会是情况一、二、三、四当中的任何一种。
在该情况下,我们直接将brother的颜色变成红色,此时根据parent的颜色决定红黑树的调整是否结束,若parent的颜色是红色,则我们将parent变为黑色后即可结束红黑树的调整;若parent的颜色原本就是黑色,则我们需要将parent结点当作下一次调整时的cur结点进行情况分析,并且情况二在下一次调整时可能会是情况一、二、三、四当中的任何一种。
情况三:brother为黑色,且其左孩子是红色结点,右孩子是黑色结点或为空。
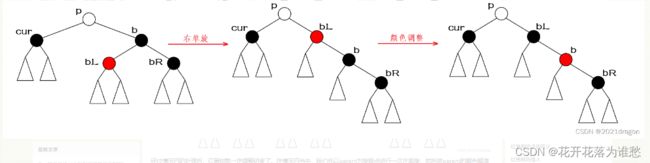 出现该情况时,我们先以brother为旋转点进行一次右单旋,再将brother结点变为红色,将brotherLeft变为黑色,此时我们再对待删除结点cur进行情况分析,情况三就转换成了情况四。
出现该情况时,我们先以brother为旋转点进行一次右单旋,再将brother结点变为红色,将brotherLeft变为黑色,此时我们再对待删除结点cur进行情况分析,情况三就转换成了情况四。
情况四:brother为黑色,且其右孩子是红色结点。
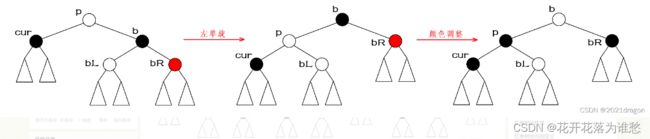 经过情况四的处理后,红黑树就一定调整结束了。在情况四当中,我们先以parent为旋转点进行一次左单旋,然后将parent的颜色赋值给brother,再将parent的颜色变为黑色,最后将brotherRight变为黑色,此时红黑树的调整便结束了。
经过情况四的处理后,红黑树就一定调整结束了。在情况四当中,我们先以parent为旋转点进行一次左单旋,然后将parent的颜色赋值给brother,再将parent的颜色变为黑色,最后将brotherRight变为黑色,此时红黑树的调整便结束了。
说明一下:
待删除结点是其父结点的右孩子时的四种情况与上面四种情况类似,这里就不列举出来了。
若待删除结点没有父结点,即待删除结点是根结点时,在找到该结点时就进行了删除,这里不用考虑,具体看代码。
这里有必要对各种情况的切换进行说明,你可能会担心调整红黑树时在这四种情况当中一直来回切换而不能跳出,下面我们来对此进行分析:

首先,进入情况四后红黑树就一定调整结束了。其次,进入情况三后,下次也一定会进入情况四,红黑树的调整也会结束。所以情况三和情况四是没有问题的,你们最纠结的只能是情况一和情况二了。
情况一又会切换为情况二、三、四,因此只要情况二能够有办法退出,那么所有情况就都能退出了。
在情况二当中我们说,如果parent的颜色是红色,那么我们将parent变为黑色后就可以结束红黑树的调整,那会不会每次进入情况二时parent的颜色都不是红色,而一直是黑色的呢?
当然有可能,但是我们若一直往上进行调整时,那么总会调整到红黑树的根结点,当调整到根结点后我们便不用进行调整了,此时根结点虽然是黑色的,但是不影响,这仅仅意味着每条从根到叶子的路径上包含的黑色结点的个数都增加了一个,此时也没有破坏红黑树的性质,也就完成了红黑树的调整,因此在调整过程中不会出现一直在这四种情况来回切换而不能跳出的问题。
第三步:进行结点的实际删除
在红黑树调整完毕后,我们就可以进行结点的删除了,删除结点的方式很简单,若待删除结点有左孩子或右孩子,我们将其左孩子或右孩子连接到待删除结点父结点的下面即可,之后便可以将待删除结点删除了。
代码的话,我就放一下我看到比较符合面向对象的一份模板吧,我自己也还在学习中,有啥问题可以一起探讨哦。如果侵权联系我删除哟3
原文链接:https /blog.csdn.net/hahahahahaha5/article/details/122507258**
#include ————————————————
相关引用
CSDN博主「小七mod」原文链接:https://blog.csdn.net/cy973071263/article/details/122543826 ↩︎
原文链接:https://blog.csdn.net/chenlong_cxy/article/details/121481859 ↩︎
原文链接:https /blog.csdn.net/hahahahahaha5/article/details/122507258 ↩︎

