Codeforces Round #776 (Div. 3) (A-E题解)

源代码:ACM/OpenjudgeNow/Codeforces at master · abmcar/ACM (github.com)

更好的阅读体验: Codeforces Round #776 (Div. 3) (A-E题解) - Abmcar’s 茶水间

A. Deletions of Two Adjacent Letters

题目大意:

思路:

题目给出了最终剩下的字母,那么我们可以判断该字母在原串中的位置,如果它前面和后面的字母数都是偶数,则可以传唤

代码:

void solution()
{
    string oriS;
    char targetChar;
    cin >> oriS >> targetChar;
    for (int i = 0; i < oriS.size(); i++)
    {
        if (oriS[i] == targetChar && i % 2 == 0 && (oriS.size() - i) % 2)
        {
            cout << "YES" << endl;
            return;
        }
    }
    cout << "NO" << endl;
}

B. DIV + MOD

题目大意:

思路:

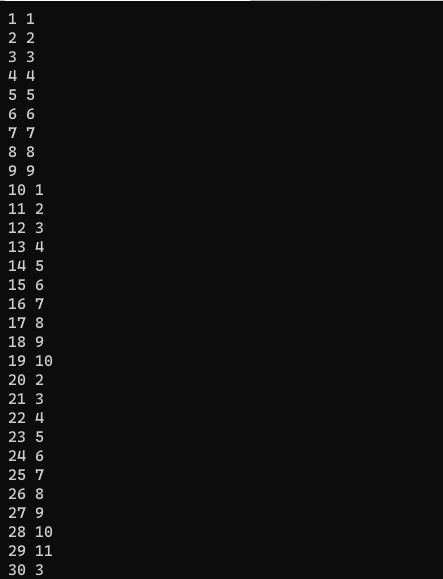
首先我们打一个表找找规律

上面是x=10的情况,发现每10个数是一个递增区间,且k*x-1是一个区间的最大值,

那么我们可以寻找最靠近右端点的最大值

$maxPos=\lfloor \frac{r}{x}\rfloor \ast x-1$

可以知道 如果maxPos不在区间$[l,r]$内 那么最大值为$f(r)$,否则,最大值为$f(maxPos)$

代码:

void solution()
{
    cin >> l >> r >> x;
    int p = r / x * x - 1;
    int ans = r / x + r % x;
    if (p >= l && p <= r)
        ans = p / x + p % x;
    cout << ans << endl;
}

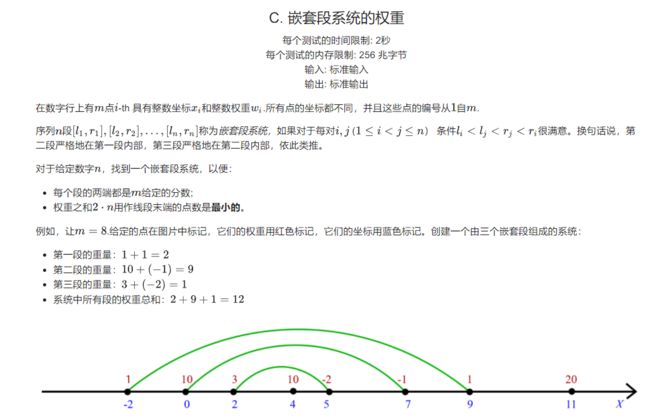
C. Weight of the System of Nested Segments

题目大意:

思路:

结构体排序板子题大概

首先排序一遍选出最大的2*n个点

之后按照坐标排序,每次输出正数第i个和倒数第i个

值得注意的是我们可以使用array和lambda简化我们的代码

代码:

使用的labmda表达式
lambda表达式(匿名函数)的简单使用 - Abmcar’s 茶水间

void solution()
{
    cin >> n >> m;
    vector<array<int, 3>> points(m), pos;
    for (int i = 0; i < m; i++)
    {
        int t1, t2;
        cin >> t1 >> t2;
        points[i] = {i + 1, t1, t2};
    }
    sort(points.begin(), points.end(), [](array<int, 3> a, array<int, 3> b) { return a[2] < b[2]; });
    int ans = 0;
    for (int i = 0; i < 2 * n; i++)
    {
        pos.push_back(points[i]);
        ans += points[i][2];
    }
    sort(pos.begin(), pos.end(), [](array<int, 3> a, array<int, 3> b) { return a[1] < b[1]; });
    cout << ans << endl;
    for (int i = 0; i < n; i++)
        cout << pos[i][0] << " " << pos[2 * n - i - 1][0] << endl;
    cout << endl;
}

D. Twist the Permutation

题目大意:

思路:

难度在于读题大概,别的就是stl板子题

仔细读题后发现移动后和它一起移动的数相对位置不会改变

因为从后往前推,从大到小枚举i,如果i不在末尾,那么在i前面的数一定是从上一次操作来的,操作数为前面的数的个数,之后我们可以手动把前面的数push到末端并pop到i,此时即为上一个状态

可以用deque实现这个功能

代码

void solution()
{
    cin >> n;
    vector<int> nums(n), ans(n + 1);
    deque<int> Q;
    for (int i = 0; i < n; i++)
    {
        cin >> nums[i];
        Q.push_back(nums[i]);
    }
    for (int i = n; i >= 1; i--)
    {
        if (Q.back() == i)
        {
            Q.pop_back();
            continue;
        }
        while (Q.front() != i)
        {
            ans[i]++;
            Q.push_back(Q.front());
            Q.pop_front();
        }
        ans[i]++;
        Q.pop_front();
    }
    for (int i = 1; i <= n; i++)
        cout << ans[i] << " \n"[i == n];
}

E. Rescheduling the Exam

题目大意:

思路:

一道看起来并不难的题

我们可以发现它移动的必定是相距最近的两个端点的其中一个,因为移动其他点后最小价值不会大

由此题目转化为在一个数组里插数使得最小间隔最大

显然可以使用二分答案来解决这个问题,回过头来想一想,其实可以枚举每一个区间来插入,寻找一个当前的最大区间/2即为新的区间

除此之外,还需要跟原最小区间和放在开头末尾的情况比较

代码:

int cnt(vector<int> &schedule)
{
    int mx = 0, mn = 1e9;
    for (int i = 1; i < n; ++i)
    {
        mx = max(mx, schedule[i] - schedule[i - 1] - 1);
        mn = min(mn, schedule[i] - schedule[i - 1] - 1);
    }
    return min(mn, max(d - schedule.back() - 1, (mx - 1) / 2));
}

void solution()
{
    cin >> n >> d;
    int minn = d;
    int minp = 0;
    int ans = 0;
    vector<int> nums(n + 1);
    for (int i = 1; i <= n; i++)
    {
        cin >> nums[i];
        if (nums[i] - nums[i - 1] <= minn)
        {
            minn = nums[i] - nums[i - 1];
            minp = i;
        }
    }
    // 另一个端点
    vector<int> schedule;
    for (int i = 0; i <= n; i++)
    {
        if (i == minp)
            continue;
        schedule.push_back(nums[i]);
    }
    ans = cnt(schedule);
    
    if (minp > 1)
    {
        schedule[minp - 1] = nums[minp];
        ans = max(ans, cnt(schedule));
    }
    cout << ans << endl;
}