使用动态规划解决最长公共子序列问题

一、定义：

给定两个序列X和Y，如果Z既是X的子序列也是Y的子序列，那么我们称Z是X和Y的公共子序列。例如：X={a,b,c,e,d,g,f}，Y={b,e,f,g},那么Z={b}、Z={b,e}、Z={b,e,f}都是X和Y的公共子序列，其中Z={b，e，f}是X和Y的最长公共子序列。求解X和Y的最长公共子序列就是LCS问题。最长公共子序列不唯一，但是其长度是唯一的。

二、定理：

令X={x1,x2,...,xm}和Y={y1,y2,....yn}为两个序列，Z={z1,z2,...zk}为这两个序列的最长公共子序列，则：

①如果xm=yn,那么zk = xm = yn，且Z(k-1)是X(m-1)和Y(n-1)的一个最长公共子序列；

②如果xm != yn，zk != xm，那么Z(k-1)是X(m-1)和Yn的一个最长公共子序列；

③如果xm != yn，zk != yn，那么Z(k-1)是Xm和Y(n-1)的一个最长公共子序列；

这样我们在求解X和Y的LCS时，可以分解为求解一个或两个这样的子问题。当xm = yn，我们需要求解X(m-1)和Y(n-1)的LCS；当xm != yn时，我们需要求解X(m-1)和Yn的一个LCS，以及求解Xm和Y(n-1)的一个LCS，两个较长者既为X和Y的LCS。

三、求解步骤：

如果用暴力搜索法求解LCS问题，就要穷举X的所有子序列，对于每个子序列都要检查它是否也是Y的子序列，从而找到最长子序列。X的每个子序列对应下表集合{1,2,3，....，m}，所以X有2^m个子序列，因此暴力搜索法的运行时间为指数阶，对较长的序列是不适用的，但是根据以上定理，LCS问题具有最优子结构性质。

我们定义一个二维数组c[i][j]用来记录Xi和Yj的LCS的长度。如果i=0，或者j=0，既一个序列长度为0，那么LCS的长度为0。根据最优子结构性质，可得如下公式

  

上述公式适用于字符串下标为0时存储的是字符串的长度，然而我们常见的字符串是'\0'为结尾的，下标为0的内容存储的并不是字符串的长度，因此我们把公式稍作修改以适应解决我们常见的字符串

根据以上公式我们，可以用动态规划方法自顶向上地计算c[i][j]的值。

以下为计算c[i][j]的值，并给出测试程序：

#include 
#define MAX_LEN 100
using namespace std;
/*给定两个字符串X和Y，求出Xi和Yj的最长公共子序列的长度，记录在c[i][j]数组中*/
void get_lcslength(const char X[],int Xlen, const char Y[],int Ylen, int c[][MAX_LEN]);

int main()
{
	
	char X[] = "abaddc";
	char Y[] = "badcaef";

	int m = strlen(X);
	int n = strlen(Y);
	int c[MAX_LEN][MAX_LEN];

	get_lcslength(X, m, Y, n, c);
	for (int i = 0; i < m;i++)
	{
		for (int j = 0; j < n;j++)
		{
			cout << c[i][j] <<"	";
		}
		cout << endl;
	}
	return 0;
}
void get_lcslength(const char X[],int Xlen, const char Y[],int Ylen, int c[][MAX_LEN])
{
	int i = 0, j = 0;
	/*初始化第0行，如果X[0]=Y[i]，则说明LCS的长度为1*/
	while (i < Ylen && X[0] != Y[i])
	{
		c[0][i] = 0;
		i++;
	}

	for (; i < Ylen; i++)
		c[0][i] = 1;
	/*同理，初始化第0列*/
	while (j < Xlen && Y[0] != X[j])
	{
		c[j][0] = 0;
		j++;
	}

	for (; j < Xlen; j++)
		c[j][0] = 1;

	for (i = 1; i < Xlen;i++)
	{
		for (j = 1; j < Ylen;j++)
		{
			if (X[i] == Y[j])
				c[i][j] = c[i - 1][j - 1] + 1;
			else if (c[i - 1][j] >= c[i][j - 1])
				c[i][j] = c[i - 1][j];
			else
				c[i][j] = c[i][j - 1];
		}
	}
}
 
  
 
  
 
  
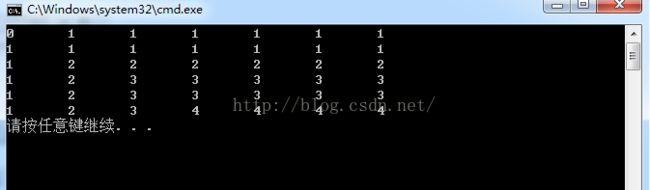
 程序的运行结果如下： 
  
 
  
我们一张表格来解释上面的程序：
 
  
 
  
 
  
第i行和第j列记录了c[i][j]的值，对于第0行第0列X[0] != Y[0]，故c[0][0]=0,对于第0行第1列，X[0]=Y[1]，因此c[0][1]=1，那么第0行从第1列开始及以后的列都为1；同理可求出第0列的所有c[i][0]的值。对于i>0，j>0的，标项c[i][j]的值取决于X[i]是否等于Y[j]及c[i-1][j-1]、c[i-1][j]、c[i][j-1]的值，这些值都会在计算c[i][j]的值之前计算出来。c[5][6]记录了X和Y的LCS的长度。
 
  
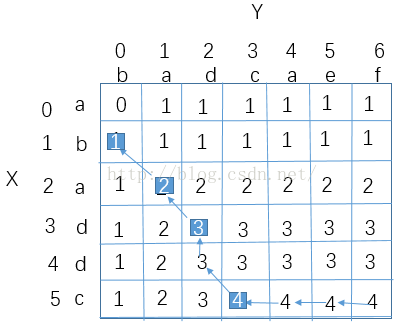
当我们求出二维数组c的值之后，我们可以根据这个二维数组求解LCS，通过上述分析我们可以了解到：c[i][j]的值只取决于c[i-1][j-1]、c[i-1][j]、c[i][j-1]这三项，给出c[i][j]的值我们可以在O(1)时间内判断出计算c[i][j]的值使用了这三项中的哪一项，我们配合下面的图说明一下算法的实现原理：
 
  
 
  
图中的箭头表示当计算c[i][j]时所使用的上一个元素是谁，首先c[i][j]与c[i][j-1]作比较，如果相等则表明计算c[i][j]时使用的是c[i][j-1]，此时令j=j-1；否则，c[i][j]与c[i-1][j]作比较，如果相等则表明计算c[i][j]时使用的是c[i-1][j]，此时令i=i-1；否则表明计算c[i][j]时使用的是c[i-1][j-1]，那么这时X[i] == Y[j]，将这个相等的字符记录到str数组中，并令j=j-1，i=i-1。进行循环比较直到i、j有一个出现0时为止。代码如下：
 
  
 
  
#include 
#define MAX_LEN 100
using namespace std;
/*给定两个字符串X和Y，求出Xi和Yj的最长公共子序列的长度，记录在c[i][j]数组中*/
void get_lcslength(const char X[],int Xlen, const char Y[],int Ylen, int c[][MAX_LEN]);
/*给定两个字符串X和Y，将最长公共子序列保存在str数组中*/
char *lcs(const char X[], const char Y[], char str[]);
int main()
{
	
	char X[] = "abaddc";
	char Y[] = "badcaef";
	char str[MAX_LEN];
	lcs(X, Y, str);
	cout << "最长公共子序列为：" << str << "	长度为：" << strlen(str)<= c[i][j - 1])
				c[i][j] = c[i - 1][j];
			else
				c[i][j] = c[i][j - 1];
		}
	}
}

char *lcs(const char X[], const char Y[], char str[])
{
	int Xlen = strlen(X);
	int Ylen = strlen(Y);
	int c[MAX_LEN][MAX_LEN];

	get_lcslength(X, Xlen, Y, Ylen, c);
	
	int i = Xlen - 1;
	int j = Ylen - 1;

	str[c[i][j]] = '\0';//此时的c[i][j]记录着最长公共子序列的长度，让str以'\0'结尾

	while (i > 0 && j > 0)
	{
		if (c[i][j] == c[i][j - 1])
			j = j - 1;
		else if (c[i][j] == c[i - 1][j])
			i = i - 1;
		else
		{
			str[c[i][j] - 1] = X[i];
			i = i - 1;
			j = j - 1;
		}
	}
	/*判断第0行或者第0列的值，如果为1则表明X[i] == Y[j]*/
	if (c[i][j] == 1)
	{
		if (i == 0)
		{
			str[0] = X[0];
		}
		if (j == 0)
		{
			str[0] = Y[0];
		}
	}
		
	return str;
}
 
  
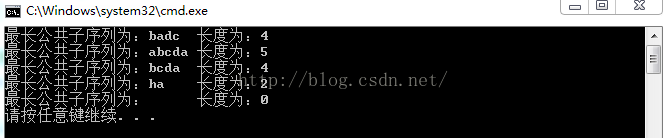
程序的运行结果如下所示：