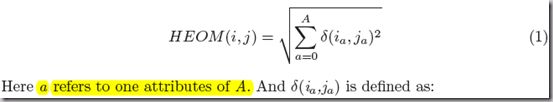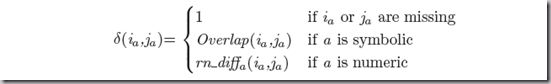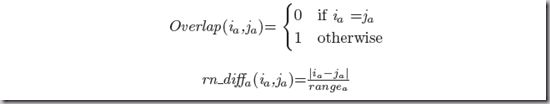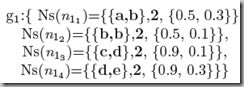Node Signature用于Attributed Graph Matching

法国University of Nancy的Salim Jouili and Salvatore Tabbone写的一篇文章Attributed Graph Matching using Local Descriptions，发表在Advanced Concepts For Intelligent Vision Systems, Proceedings,2009，不算很牛，在web of science上引用为3，且多自引，由于跟我做的课题十分相关，所以姑且一读。

 

文章主要有三点：

1 用简单向量Node Signature来描述attributed graph (AG)

each graph is represented by a set of local descriptions which are related to the node features and used to compute the node-to-node distance

每个点的Node Signature是a set composed by three subsets：

1)node attribute(s), 2)the node degree and 3)the attributes of the incident edges to this node

 

具体计算：

Given a graph G = (V, E, A) where

 

2 采用Heterogeneous Euclidean Overlap Metric(HEOM)来衡量两个Node Signature之间的距离

至于距离度量，numeric attributes可以用Euclidean and Manhattan distance metrics, 而symbolic attributes可以用the Overlap distance。而处理两者兼有的数据类型，就需要heterogenous distance function。一种基于value difference metric (e.g. Heterogeneous Value Difference Metric)，一种基于Euclidean distance (e.g. Heterogeneous Euclidean Overlap Metric, HEOM).前者只在classification context下使用， by introducing class information into the distance formula.因此文中使用HEOM。

The HEOM uses 1)the overlap metric for symbolic attributes and 2)the normalized Euclidean distance for numeric attributes.

A is the attribute set that contains unary attribute ai and binary attribute aij.The overall distance between two heterogeneous node signatures i and j is given by the function HEOM(i,j ):

The function Overlap and the rang-normalized difference rn diffa are defined as:

range_a是用来对属性进行归一化的，使得rang-normalized difference几乎都小于1。

详见D.R. Wilson, T.R. Martinez, Improved heterogeneous distance functions, Journal
of Artificial Intelligence Research, vol. 6, no. 1, pp. 1-34, 1997.

 

3 然后就得到一个cost matrix describes the matching costs between nodes in two graphs，把这个bipartite graph matching问题看做一个assignment problem，用Hungarian method 寻找optimum matching，复杂度(n is the size of the biggest graph)。

the attributed graph matching are implemented as a following 2-steps procedure:

Firstly, similarities between every pair of nodes in two graphs, forming a distance matrix, are computed using a predefined measure.

These distances form a cost matrix which defines a node-to-node assignment for a pair of graphs.

Secondly, the matching between nodes is based on the distance matrix by using an approximate algorithm such as the bipartite matching [3].

Therefore, the attributed graph matching problem is mathematically formulated as an assignment
problem.

 

M是一个matching function，其中=表示点指派给点；否则该项为0。等于两图中较小者的大小。定义，为M所指定的匹配的matching cost.

这个最终的distance代表了经过matching size来正则化的matching cost，并且随着两图size大小的差异增大而增大(|gi| is the size(number of nodes) of the graph gi)。

This distance represents the matching cost normalized by the matching size,
and is increased by the difference of sizes of the two graphs We can demonstrate that this distance is a
metric satisfying non-negativity, identity of indiscernible, and symmetry triangle
inequality conditions.

 

 

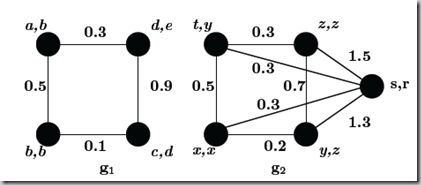
举个例子

两个属性图g1 和 g2

点属性是symbolic的，边属性是numeric的，则两图各自node signature为

例如可以计算得到间的距离为

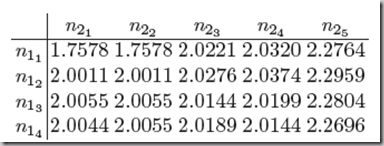
如此可以得到cost matrix

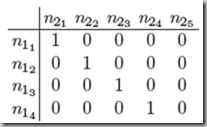
通过hungarian algorithm得到最佳分配

因此g1和g2间的距离就是