在R中使用支持向量机(SVM)(1)
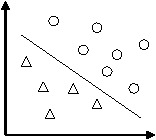
假设有分布在Rd空间中的数据,我们希望能够在该空间上找出一个超平面(Hyper-pan),将这一数据分成两类。属于这一类的数据均在超平面的同侧,而属于另一类的数据均在超平面的另一侧。如下图。
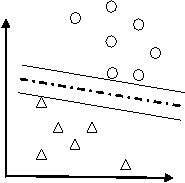

比较上图,我们可以发现左图所找出的超平面(虚线),其两平行且与两类数据相切的超平面(实线)之间的距离较近,而右图则具有较大的间隔。而由于我们希望可以找出将两类数据分得较开的超平面,因此右图所找出的是比较好的超平面。可以将问题简述如下:
设训练的样本输入为xi,i=1,…,l,对应的期望输出为yi∈{+1,-1},其中+1和-1分别代表两类的类别标识,假定分类面方程为ω﹒x+b=0。为使分类面对所有样本正确分类并且具备分类间隔,就要求它满足以下约束条件:
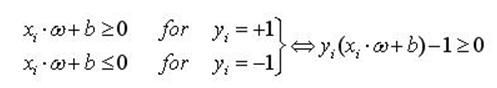 (1)
(1)
可以计算出,分类间隔为
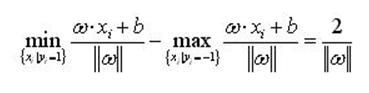 (2)
(2)
在约束式的条件下最大化分类间隔2/||ω||这可以通过最小化||ω||2的方法来实现。那么,求解最优平面问题可以表示成如下的约束优化:即在条件式(1)的约束下,最小化函数
 (3)
(3)
为了解决约束最优化问题,引入式(3)的拉格朗日函数
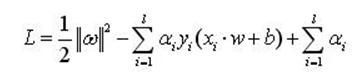 (4)
(4)
其中,αi>0为拉格朗日系数,现在的问题就是关于ω和b求L的最小值。
把式(4)分别对ω和b求偏微分并令其等于0,就可以把上述问题转化为一个较简单的"对偶"形式:
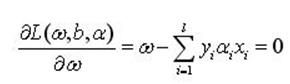 (5a)
(5a)
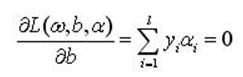 (5b)
(5b)
将得到的关系式:
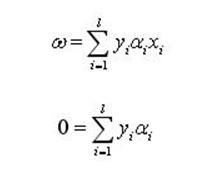 (6)
(6)
代入到原始拉格朗日函数,得到:
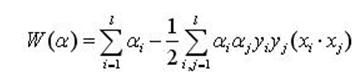 (7)
(7)
如果αi*为最优解,那么
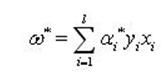 (8)
(8)
即最优超平面的权系数向量是训练样本向量的线性组合。
由于上述优化问题是一个Convex Problem,求解上述的SVM问题,须满足KKT条件,这个优化问题的解必须满足
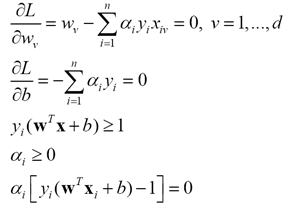 (9)
(9)
因此,对多数样本ai将为0,取值不为零的ai对应于式(1)中等号成立的样本即支持向量。
求解上述问题后得到的最优分类函数是
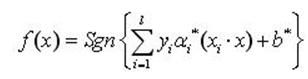 (10)
(10)
由于非支持向量对应的ai均为0,因此上式的求和实际上只对支持向量进行。最终的优化问题为
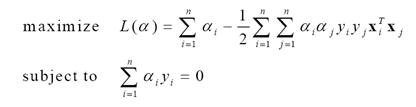 (11)
(11)
2. 非线性SVM

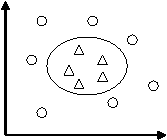
然而有的问题并不是线性可分的。但是可以通过一个适当的非线性函数φ,将数据由原始特征空间映射到一个新的特征空间,然后在新空间中寻求最优判定超平面。
所以问题(11)可以改写为
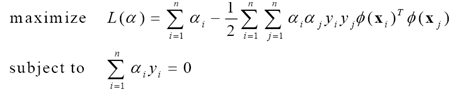 (12)
(12)
如果直接在高维空间计算φ(x),将会带来维数灾难。为了解决这一问题,引入核函数
 (13)
(13)
这样问题(12)就变成
 (14)
(14)
常用的核函数有
-
多项式核
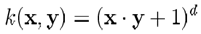
-
高斯径向基核
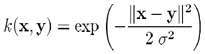
-
Sigmoid核

实际问题很少线性可分,虽然理论上可通过非线性映射得到线性可分的数据,但如何获得这样的映射,且避免过拟合,仍存在问题。所以更实际的策略是允许一定误差。通常引入松弛变量ε,放松约束。这时问题描述改为下面的形式
 (15)
(15)
这样的分类器称为线性软间隔支持向量分类机。转化为拉格朗日乘子待定问题
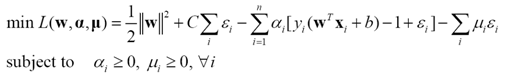
其KKT条件为
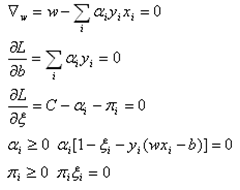 (17)
(17)
得到
 (18)
(18)
只要确定a,便可解出w,b.
将上述条件代入L中,得到新的优化问题:
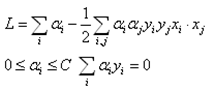 (19)
(19)
同样地引入核函数,把这个软间隔SVM的训练表示为一个高维空间上的二次规划问题
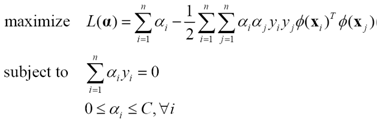 (20)
(20)
非线性SVM可用经典的二次规划方法求解,但同时求解n个拉格朗日乘子涉及很多次迭代,计算开销太大。所以一般采用Sequential Minimal Optimization(SMO)算法。其基本思路是每次只更新两个乘子,迭代获得最终解。计算流程可表示如下
For i=1:iter
-
根据预先设定的规则,从所有样本中选出两个
-
保持其它拉格朗日乘子不变,更新所选样本对应的拉格朗日乘子
End
SMO算法的优点在于,只有两个变量的二次规划问题存在解析解。
关键的技术细节在于,一是在每次迭代中,怎样更新乘子;二是怎样选择每次迭代需要更新的乘子。
假定在某次迭代中,需要更新样本x1,x2对应的拉格朗日乘子a1,a2.
这个小规模的二次规划问题可以写成
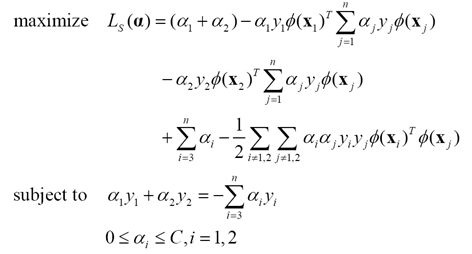
进一步简化为
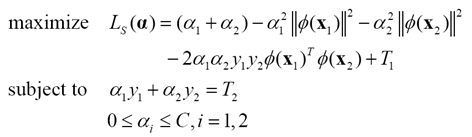
步骤1 计算上下界L和H
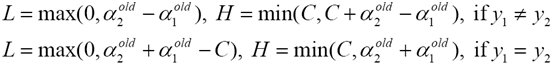
步骤2 计算Ls的二阶导数

步骤3 更新a2
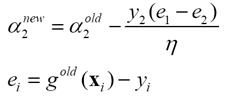
步骤4 计算中间变量
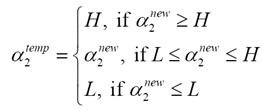
步骤5 更新a1
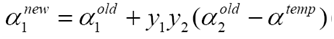
选择需要更新的乘子需要满足两点。
-
任何乘子必须满足KKT条件
-
对一个满足KKT条件的乘子进行更新,应能最大限度增大目标函数的值(类似于梯度下降)
SMO算法的优点,在于
(1)可保证解的全局最优性,不存在陷入局部极小解的问题。
(2)分类器复杂度由支撑向量的个数,而非特征空间的维数决定,因此较少因维数灾难发生过拟合现象。
缺点是需要求解二次规划问题,其规模与训练量成正比,因此计算复杂度高,且存储开销大, 不适用于需进行在线学习的大规模分类问题。
Suykens和Vandewalle1999年提出
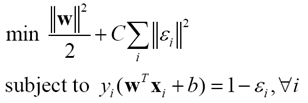 (23)
(23)
与SVM的关键不同是约束条件由不等式变为了等式,对应的优化问题
 (24)
(24)
不等式变为等式后,拉格朗日乘子可以通过解线性系统得到
 (25)
(25)
解线性系统远易于解二次规划问题。但相应地,绝大部分拉格朗日乘子都将不为零。也就是说,LS-SVM分类器的测试时间将长于SVM分类器。
机器学习问题是在已知n个独立同分布的观测样本,在同一组预测函数中求一个最优的函数对依赖关系进行估计,使期望风险R[f]最小。期望风险的大小直观上可以理解为,当我们用f(x)进行预测时,"平均"的损失程度,或"平均"犯错误的程度。损失函数是评价预测准确程度的一种度量,它与预测函数f(x)密切相关。而f(x)的期望风险依赖于概率分布和损失函数,前者是客观存在的,后者是根据具体问题选定的,带有(主观的)人为的或偏好色彩。
但是,只有样本却无法计算期望风险,因此,传统的学习方法用样本定义经验风险Remp[f]作为对期望风险的估计,并设计学习算法使之最小化。即所谓的经验风险最小化(Empirical Risk Minimization, ERM)归纳原则。经验风险是用损失函数来计算的。对于模式识别问题的损失函数来说,经验风险就是训练样本错误率;对于函数逼近问题的损失函数来说,就是平方训练误差;而对于概率密度估计问题的损失函数来 说,ERM准则就等价于最大似然法。事实上,用ERM准则代替期望风险最小化并没有经过充分的理论论证,只是直观上合理的想当然做法。也就是说,经验风险最小不一定意味着期望风险最小。其实,只有样本数目趋近于无穷大时,经验风险才有可能趋近于期望风险。但是很多问题中样本数目离无穷大很远,那么在有限样本下ERM准则就不一定能使真实风险较小。ERM准则不成功的一个例子就是神经网络的过学习问题(某些情况下,训练误差过小反而导致推广能力下降,或者说是训练误差过小导致了预测错误率的增加,即真实风险的增加)。
因此,在有限样本情况下,仅仅用ERM来近似期望风险是行不通的。统计学习理论给出了期望风险R[f]与经验风险Remp[f]之间关系:R[f] <= ( Remp[f] + e )。其中 e = g(h/n) 为置信区间,e 是VC维 h 的增函数,也是样本数n的减函数。右端称为结构风险,它是期望风险 R[f] 的一个上界。经验风险的最小依赖较大的F(样本数较多的函数集)中某个 f 的选择,但是 F 较大,则VC维较大,就导致置信区间 e 变大,所以要想使期望风险 R[f] 最小,必须选择合适的h和n来使不等式右边的结构风险最小,这就是结构风险最小化(Structural Risk Minimization, SRM)归纳原则。实现SRM的思路之一就是设计函数集的某种结构使每个子集中都能取得最小的经验风险(如使训练误差为0),然后只需选择适当的子集使置信范围最小,则这个子集中使经验风险最小的函数就是最优函数。SVM方法实际上就是这种思想的具体实现。
SVM是一种基于统计的学习方法,它是对SRM的近似。概括地说,SVM就是首先通过用内积函数定义的非线性变换将输入空间变换到一个高维空间,然后再在这个空间中求(广义)最优分类面的分类方法。