pytorch构建深度网络的基本概念——随机梯度下降
文章目录
- 随机梯度下降
-
- 定义一个简单的模型
- 定义Loss
- 什么是梯度
- 随机梯度下降
随机梯度下降
现在说说深度学习中的权重更新算法:经典算法SGD:stochastic gradient descent,随机梯度下降。
定义一个简单的模型
假设我们的模型就是要拟合一根直线:
那么直线的方程为:
y = ω x + b y = \omega x + b y=ωx+b
而且我们的训练集有 n n n个样本:
( x 1 , y 1 ) , . . . . ( x n , y n ) {(x_1, y_1), .... (x_n, y_n)} (x1,y1),....(xn,yn)
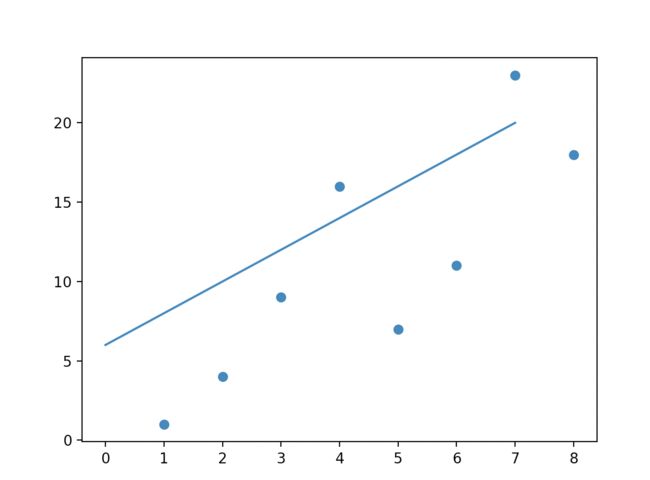
如图所示:
更简单一点,假设这根直线穿过原点,那么后面的常数b也没有了
我们通过图中的这些样本点去训练模型获得靠谱的 w w w。
定义Loss
在反向传播的基本逻辑里,首先要定义一个损失函数,损失函数其实就是预测值与真实值(训练数据)的差异,在这个例子里,我们定义的这个差异是均方误差,用公式表示就是:
l = ( y i − y i ^ ) 2 l = ({y_i} - \hat{y_i})^2 l=(yi−yi^)2
那么,联合上面两个公式可以得到:
l = w x i 2 − 2 w x i y i ^ − y i ^ 2 l = {wx_i }^2 - 2wx_i\hat{y_i} -\hat{y_i}^2 l=wxi2−2wxiyi^−yi^2
我们就是要通过这个误差去反向计算 w w w的调整量。
我们在训练的时候,一般来说都是一批数据一起调整,每次都调整也太费劲了,作为一个batch,用一个batch的样本损失的平均值来进行权重调整。
一个batch的每个样本都有一个损失:对这些损失求和,比如一个batch有m个样本
e = ∑ i m = 1 m ( ( x 1 2 + . . . + x m 2 ) ∗ w 2 + ( − 2 ∗ x 1 ∗ y 1 + . . . + − 2 ∗ x m ∗ y + m ) ∗ w + ( y 1 2 + . . . + y m 2 ) ) e = \sum_i^m=\frac{1}{m}(({x_1^2 + ... + x_m^2})*w^2 + (-2*x_1*y_1 + ... + -2*x_m*y+m)*w + (y_1^2 + ... +y_m^2)) e=i∑m=m1((x12+...+xm2)∗w2+(−2∗x1∗y1+...+−2∗xm∗y+m)∗w+(y12+...+ym2))
如果令
a = x 1 2 + . . . + x m 2 a = {x_1^2 + ... + x_m^2} a=x12+...+xm2
b = ( − 2 ∗ x 1 ∗ y 1 + . . . + − 2 ∗ x m ∗ y + m ) b = (-2*x_1*y_1 + ... + -2*x_m*y+m) b=(−2∗x1∗y1+...+−2∗xm∗y+m)
c = ( y 1 2 + . . . + y m 2 ) c = (y_1^2 + ... +y_m^2) c=(y12+...+ym2)
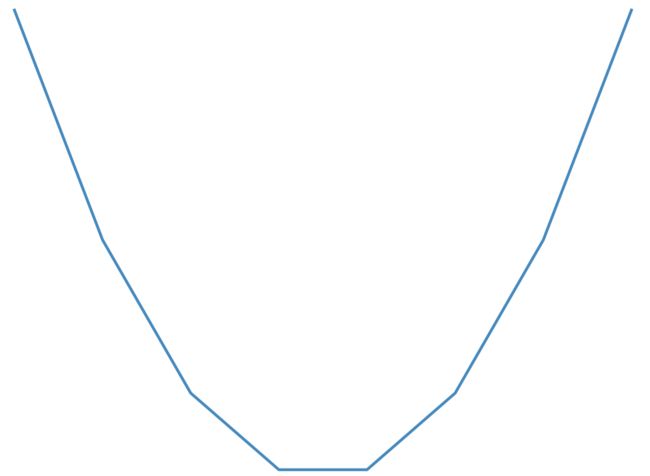
那么上面公式实际上就是以 w w w为变量的二次方程,图像是一个朝上的U型曲线,因为 a a a肯定大于0。那么这个二次曲线图可以如图(matplot画的图,不够细致,大概那个意思):
什么是梯度
上面已经把模型的输出损失定义和公式列举出来了。
那么为了尽快收敛,也就是为了尽快的让 w w w能达到我们想要的目标,也就是上面这个曲线的最低处(极值),我们就会让当前的梯度(初始化可能是一个正态分布或者随机数)加上某个偏移量,那么这个偏移量是多少呢,就是对上面的值就行求导,求导也就是求梯度。
梯度的正方向是远离极值的方向,所以需要取个负号,所以也叫梯度下降。用公式表示就是:
θ = − ∂ e ∂ l = − 1 n ( a w + b ) \theta = -\frac{\partial e}{\partial l} = -\frac{1}{n}(aw + b) θ=−∂l∂e=−n1(aw+b)
我这里为了省事,把b去掉了,有兴趣的可以带入进去算一下,因为对 w w w求偏导的时候, b b b就是个常量,求完就直接等于0了。
上面公式计算出来的就是曲线当前点的梯度,或者说是切线的斜率。那么沿着斜率走多少了?也就是最终还是要求出一个 Δ w \Delta w Δw来,这就是训练中的参数学习率了,在学习率 η \eta η的情况下(可以理解成斜率上的x轴距离),权重的调整量就是:
w ^ = w + Δ w = w + η ∗ θ \hat{w}=w+\Delta{w} = w + \eta * \theta w^=w+Δw=w+η∗θ
随机梯度下降
随机是指上面的这个batch是在整个训练集随机挑选样本到batch中,这个就可以减小样本之间造成的参数更新抵消问题。