机器学习指标计算

一、有如下图

1. accuracy

$$\text{ accuracy }=\frac{TP+TN}{TP+TN+FP+FN}$$ accuracy指的是正确预测的样本数占总预测样本数的比值，它不考虑预测的样本是正例还是负例,考虑的是全部样本。

2. precision（查准率）

$$\text{ precision }=\frac{TP}{TP+FP}$$

precision指的是正确预测的正样本数占所有预测为正样本的数量的比值，也就是说所有预测为正样本的样本中有多少是真正的正样本。从这我们可以看出，precision只关注预测为正样本的部分。

3. recall（召回率）

$$\text{ recall }=\frac{TP}{TP+FN}$$

它指的是正确预测的正样本数占真实正样本总数的比值，也就是我能从这些样本中能够正确找出多少个正样本。

4. F-score

$$F-\text{ score }=\frac{2}{1/\text{ precision }+1/\text{ recall }}$$ F-score相当于precision和recall的调和平均，用意是要参考两个指标。从公式我们可以看出，recall和precision任何一个数值减小，F-score都会减小，反之，亦然。

5. specificity

$$\text{ specificity }=\frac{TN}{TN+FP}$$ specificity指标平时见得不多，它是相对于sensitivity（recall）而言的，指的是正确预测的负样本数占真实负样本总数的比值，也就是我能从这些样本中能够正确找出多少个负样本。

6. sensitivity(TPR)

$$\text{ sensitivity }=\frac{TP}{TP+FN}=\text{ recall }$$

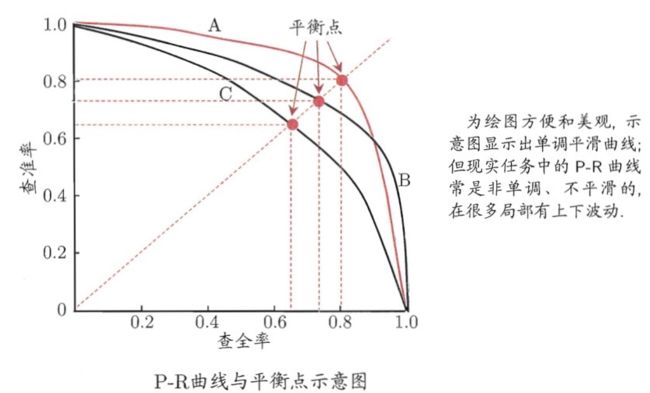
7. P-R曲线

我们将纵轴设置为precison，横轴设置成recall，改变阈值就能获得一系列的pair并绘制出曲线。对于不同的模型在相同数据集上的预测效果，我们可以画出一系列的PR曲线。一般来说如果一个曲线完全“包围”另一个曲线，我们可以认为该模型的分类效果要好于对比模型。

如下图所示：

样本不均衡下的指标

背景：

在大多数情况下不同类别的分类代价并不相等，即将样本分类为正例或反例的代价是不能相提并论的。例如在垃圾邮件过滤中，我们希望重要的邮件永远不要被误判为垃圾邮件，还有在癌症检测中，宁愿误判也不漏判。在这种情况下，仅仅使用分类错误率来度量是不充分的，这样的度量错误掩盖了样本如何被错分的事实。所以，在分类中，当某个类别的重要性高于其他类别时，可以使用Precison和Recall多个比分类错误率更好的新指标。

8. roc(Receiver Operating Characteristic Curve)

在实际的数据集中经常会出现类别不平衡现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间而变化。而在这种情况下，ROC曲线能够保持不变。同时，我们可以断言，ROC曲线越接近左上角，该分类器的性能越好，意味着分类器在假阳率很低的同时获得了很高的真阳率。

以下是一个ROC曲线的实例：

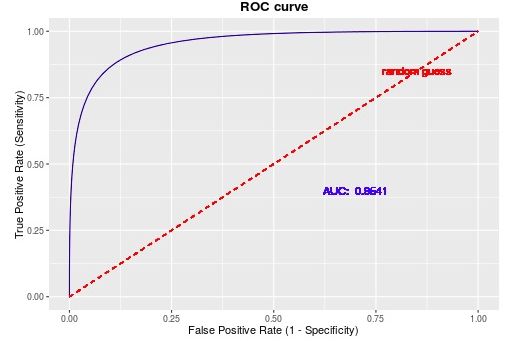
其中，该曲线的横坐标为假阳性率（False Positive Rate, FPR），N是真实负样本的个数，FP是N个负样本中被分类器预测为正样本的个数，P是真实真样本的个数。 其中 $FPR=\frac{FP}{FP+TN}$,$TPR=\frac{TP}{TP+FN}$。

举个例子，如果有20个样本的2分类，分类结果如下所示：

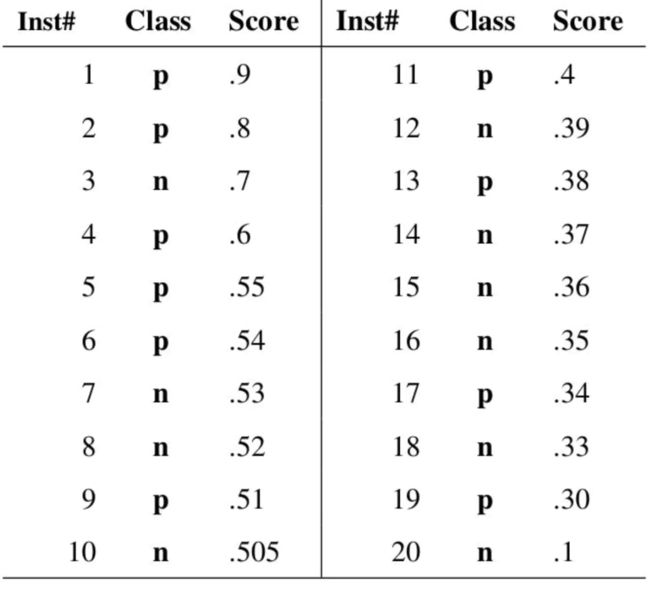
现在我们指定一个阈值为0.9，那么只有第一个样本（0.9）会被归类为正例，而其他所有样本都会被归为负例，因此，对于0.9这个阈值，我们可以计算出FPR为0，TPR为0.1（因为总共10个正样本，预测正确的个数为1），那么我们就知道曲线上必有一个点为(0, 0.1)。依次选择不同的阈值（或称为“截断点”），画出全部的关键点以后，再连接关键点即可最终得到ROC曲线如下图所示。

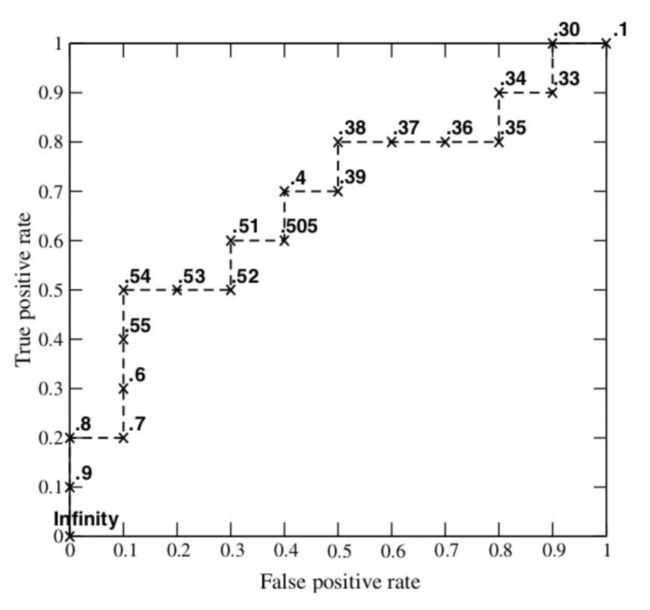
其实还有一种更直观的绘制ROC曲线的方法，就是把横轴的刻度间隔设为$\frac{1}{N}$，纵轴的刻度间隔设为$\frac{1}{P}$，N,P分别为负样本与正样本数量。然后再根据模型的输出结果降序排列，依次遍历样本，从0开始绘制ROC曲线，每遇到一个正样本就沿纵轴方向绘制一个刻度间隔的曲线，每遇到一个负样本就沿横轴方向绘制一个刻度间隔的曲线，遍历完所有样本点以后，曲线也就绘制完成了。

使用sklearn进行roc曲线绘制：

>>> from sklearnimport metrics
>>> import numpy as np
>>> y = np.array([1, 1, 2, 2]) #假设4个样本
>>> scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)
>>> fpr #假阳性
array([ 0. ,  0.5,  0.5,  1. ])
>>> tpr #真阳性
array([ 0.5,  0.5,  1. ,  1. ])
>>> thresholds #阈值
array([ 0.8 ,  0.4 ,  0.35,  0.1 ])
>>> #auc(后面会说)
>>> auc = auc = metrics.auc(fpr, tpr)
>>> auc
0.75

绘制曲线：

import matplotlib.pyplot as plt
plt.figure()
lw = 2
plt.plot(fpr, tpr, color='darkorange',
         lw=lw, label='ROC curve (area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()

所画图像如图所示：

9. auc(Area under curve)

auc指的是计算roc的面积。 AUC值是一个概率值，当你随机挑选一个正样本以及负样本，当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值，AUC值越大，当前分类算法越有可能将正样本排在负样本前面，从而能够更好地分类。

def AUC(label, pre):
　　"""
　　适用于ｐｙｔｈｏｎ3.0以上版本
   """
　　#计算正样本和负样本的索引，以便索引出之后的概率值
    pos = [i for i in range(len(label)) if label[i] == 1]
    neg = [i for i in range(len(label)) if label[i] == 0]
 
    auc = 0
    for i in pos:
        for j in neg:
            if pre[i] > pre[j]:
                auc += 1
            elif pre[i] == pre[j]:
                auc += 0.5
 
    return auc / (len(pos)*len(neg))
 
 
if __name__ == '__main__':
    label = [1,0,0,0,1,0,1,0]
    pre = [0.9, 0.8, 0.3, 0.1, 0.4, 0.9, 0.66, 0.7]
    print(AUC(label, pre))

当然，也可以使用公式来进行计算： $$AUC=\frac{{\sum }_{i\in \text{ positiveClass }}{\mathrm{rank}}_i-\frac{M(1+M)}{2}}{M\times N}$$

代码如下：

import numpy as np
def auc_calculate(labels,preds,n_bins=100):
    postive_len = sum(labels)
    negative_len = len(labels) - postive_len
    total_case = postive_len * negative_len
    pos_histogram = [0 for _ in range(n_bins)]
    neg_histogram = [0 for _ in range(n_bins)]
    bin_width = 1.0 / n_bins
    for i in range(len(labels)):
        nth_bin = int(preds[i]/bin_width)
        if labels[i]==1:
            pos_histogram[nth_bin] += 1
        else:
            neg_histogram[nth_bin] += 1
    accumulated_neg = 0
    satisfied_pair = 0
    for i in range(n_bins):
        satisfied_pair += (pos_histogram[i]*accumulated_neg + pos_histogram[i]*neg_histogram[i]*0.5)
        accumulated_neg += neg_histogram[i]

    return satisfied_pair / float(total_case)
 
 y = np.array([1,0,0,0,1,0,1,0,])
 pred = np.array([0.9, 0.8, 0.3, 0.1,0.4,0.9,0.66,0.7])
print("----auc is :",auc_calculate(y,pred))

10. AUROC (Area Under the Receiver Operating Characteristic curve)

大多数时候，AUC都是指AUROC，这是一个不好地做法，AUC有歧义（可能是任何曲线），而AUROC没有歧义。

其余部分，与AUC一致。

二. 图像分割指标汇总

1. pixel accuracy (标记正确/总像素数目)

为了便于解释，假设如下：共有$k+1$个类(从$L_0$到$L_k$，其中包含一个空类活着背景)，$p_{ij}$表示本属于类$i$但是预测成类$j$的像素数量。即，$p_{ii}$表示真正的正样本，而$p_{ij},p_{ji}$ 表示被分别被解释成假正与假负。

其计算公式如下： $$PA=\frac{{\sum }_0^k{p}_{ii}}{{\sum }_{i=0}^k{\sum }_{j=0}^k{p}_{ij}}$$
图像中共有$k+1$类，$P_{ii}$ 表示将第$i$类分成第$i$类的像素数量(正确分类的像素数量)，$P_{ij}$表示将第$i$类分成第$j$类的像素数量(所有像素数量)
因此该比值表示正确分类的像素数量占总像素数量的比例。

对于$PA$而言，优点就是简单！ 缺点：如果图像中大面积是背景，而目标较小，即使将整个图片预测为背景，也会有很高的PA得分，因此该指标不适用于评价以小目标为主的图像分割效果。

2. MPA(Mean Pixel Accuracy)

其计算公式如下： $$MPA=\frac{1}{1+K}\sum _0^k\frac{p_{ii}}{{\sum }_{j=0}^k{p}_{ij}}$$

计算每类各自分类的准确率，再取均值!

3. MIou(Mean Intersection over Union)

计算两个集合的交集与并集之比，在语义分割中，这两个集合为真实值和预测值。 $$MIoU=\frac{1}{k+1}\sum _{i=0}^k\frac{p_{ii}}{{\sum }_{j=0}^k{p}_{ij}+{\sum }_{j=0}^k{p}_{ji}-p_{ii}}$$

4. FWIoU(Frequency Weighted Intersection over Union)

MIou的一种提升，这种方法可以根据每个类出现的频率为其设置权重： $$FWIoU=\frac{1}{{\sum }_{i=0}^k{\sum }_{j=0}^k{p}_{ij}}\sum _{i=0}^k\frac{p_{ii}}{{\sum }_{j=0}^k{p}_{ij}+{\sum }_{j=0}^k{p}_{ji}-p_{ii}}$$

三. 目标检测指标汇总

主要是用到以下的指标：

$mAP$: $meanAveragePrecision$, 即各类别$AP$的平均值
$AP$: $PR$曲线下面积，后文会详细讲解
$PR$曲线: $Precision-Recall$曲线
$Precision:TP/(TP+FP)$
$Recall:TP/(TP+FN)$
$TP:IoU>0.5$的检测框数量（同一$GroundTruth$只计算一次）
$FP:IoU<=0.5$的检测框，或者是检测到同一个$GT$的多余检测框的数量
$FN$: 没有检测到的GT的数量
$IOU$: 计算两个集合的交集与并集之比
$NMS$: 非极大值抑制
$AP$计算

要计算$AP$，首先需要计算的是$TP、FP、FN$.

对于单张图片，首先遍历图片中$ground$ $truth$对象，然后提取我们要计算的某类别的$gt$ $objects$，之后读取我们通过检测器检测出的这种类别的检测框（其他类别的先不管），接着过滤掉置信度分数低于置信度阈值，也有的是未设置置信度阈值。将剩下的检测框按置信度分数从高到低排序，最先判断置信度分数最高的检测框与$gt$ $bbox$的$iou$是否大于$iou$阈值，若$iou$大于设定的$iou$阈值即判断为$TP$，将此$g{t}_{b}box$标记为已检测（后续的同一个$GT$的多余检测框都视为$FP$,这就是为什么先要按照置信度分数从高到低排序，置信度分数最高的检测框最先去与$iou$阈值比较，若大于$iou$阈值，视为$TP$，后续的同一个$gt$对象的检测框都视为$FP$），$iou$小于阈值的，为$FP$。图片中某类别一共有多少个GT是固定的，减去TP的个数，剩下的就是FN的个数了

当有了$TP,FP,FN$值之后，我们就可以计算这一类别的$precision$与$recall$。从而计算$AP$。

在$VOC2010$以前，只需要选取当$Recall>=0,0.1,0.2,...,1$共$11$个点时的$Precision$最大值，然后$AP$就是这$11$个$Precision$的平均值。
在$VOC2010$及以后，需要针对每一个不同的$Recall$值（包括0和1），选取其大于等于这些$Recall$值时的$Precision$最大值，然后计算$PR$曲线下面积作为$AP$值。
$COCO$数据集，设定多个$IOU$阈值（$0.5-0.95$,$0.05$为步长），在每一个$IOU$阈值下都有某一类别的$AP$值，然后求不同$IOU$阈值下的$AP$平均，就是所求的最终的某类别的$AP$值。
$mAP$计算

顾名思义，所有类的$AP$值平均值就是$mAP$。

四. 模型效率衡量

FLOPs(floating point operations)

假设卷积操作的实现是按照滑窗的形式，并且非线性函数是不消耗计算资源的。那么对于卷积核的$FLOPs$为： $$FLOPs=2HW(C_{in}{K}^2+1)C_{out}$$ 其中$H$,$W$与$C_{in}$是高，宽与输入特征的通道数， $K$是卷积核的宽度与长度，$C_{out}$是输出通道数。同时，假设了输入输出的尺寸是一样的。

对于全连接层： $$FLOPs=(2I-1)O$$ 其中，$I$是输入的维度，$O$是输出维度。